International Journal of Mechanics Research
Vol.
12
No.
01
(
2023
), Article ID:
63337
,
12
pages
10.12677/IJM.2023.121006
方波电流对混合簇放电的影响及其动力学分析
蒋亚璐,陈雪丽
北方工业大学理学院,北京
收稿日期:2023年2月3日;录用日期:2023年2月8日;发布日期:2023年3月30日

摘要
Pre-Bötzinger复合体(简称pre-BötC)是新生哺乳动物产生正常呼吸节律的关键部位。当神经元受到外部刺激时,其放电模式会发生改变。方波电流是最简单且易实现的一种电流形式。本文通过调控方波电流的三个变量,来研究方波电流对神经元放电模式的影响。并通过时间序列和单参数分岔分析以及双参数分岔分析的方法,探究放电模式产生及转迁的动力学机制。结果表明方波电流可以诱导神经元产生混合簇放电。本文的研究结果为进一步理解神经系统中混合簇放电的产生机制提供了有益的参考。
关键词
pre-Bötzinger复合体,方波电流,分岔,混合簇放电

Influence of Square Wave Current on Mixed Bursting and Its Dynamic Analysis
Yalu jiang, Xueli Chen
School of Science, North China University of Technology, Beijing
Received: Feb. 3rd, 2023; accepted: Feb. 8th, 2023; published: Mar. 30th, 2023

ABSTRACT
Pre-Bötzinger complex (referred to as pre-BötC) is a key site in the generation of normal respiratory rhythm in newborn mammals. When neurons are subjected to external stimuli, their firing patterns change. Square wave current is one of the simplest and easily achievable forms of current. In this paper, we investigate the effects of square current on the firing pattern of neurons by regulating three variables of square current. By time series, single-parameter bifurcation analysis and two-parameter bifurcation analysis, the dynamic mechanism of generation and transition of bursting pattern is explored. The results show that square current can induce neurons to generate mixed bursting. The findings of this paper can provide some reference for further understanding the generation mechanism of mixed bursting in the nervous system.
Keywords:Pre-Bötzinger Complex, Square Wave Current, Bifurcation, Mixed Bursting

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
关于神经元动力学的研究很多,目前已经取得了很大进展。非线性理论已被应用于神经元动力学中,以解释神经元放电模式的动力学机制 [1] [2] 。当神经元活动在静息状态和重复尖峰放电之间交替进行时,神经元活动被称为簇放电。簇放电模式与生理学意义密切相关 [2] [3] 。Pre-Bötzinger复合体(pre-BötC)中的神经元群是呼吸神经网络的重要组成部分,能产生稳定的呼吸节律 [4] [5] 。在pre-BötC模型中,已观察到pre-BötC神经元中丰富的动力学行为,特别是混合簇放电的产生 [5] [6] 。
早在1999年,Butera等人就针对pre-BötC神经元建立了两个最小模型 [7] [8] 。他们的研究表明,神经元在不同的外激励刺激下能够引起不同的簇放电模式,并且发现钠离子,持续钠离子和钾离子都是引起簇放电的原因。Rubin等人提出一个新的数学模型,证明了一种非常规的节律产生机制,Ca2+激活的非特异性阳离子电流(ICAN)可以引起全网络放电 [9] 。在后续的研究中发现,Ca2+浓度振荡可诱发树突簇,即钙电流(ICAN)可单独作用于pre-BötC上,诱导生成簇放电 [10] [11] 。钙子系统中的关键参数对pre-BötC放电模式的影响也有相关的研究 [12] [13] [14] [15] 。
之后Park和Rubin建立了pre-BötC单室模型,并对胞体簇,树突簇和混合簇产生的原因做出了解释 [16] 。钙电流,磁流等不同的外激励作用下,神经系统的节律会产生复杂的转迁。方波电流的动力学特性简单,对pre-BötC模型的动力学行为的影响特别是不同的参数对簇放电的作用,值得进一步研究。
本文结构如下:首先介绍了具有方波电流激励的pre-BötC模型;其次分析了方波电流在不同变量变化下,对神经元产生簇放电的影响。运用单参数分岔分析法,揭示了方波电流作用下簇放电模式的产生和转迁规律。最后,给出本文的结论。
2. 模型介绍
为了探究外激励对pre-BötC神经元模型中放电活动的影响,我们引入一种简单且易实现的电流,即方波电流。具有方波电流的pre-BötC单室细胞的Butera模型描述如下:
(1)
(2)
(3)
其中,V是膜电位,n和h是钾和钠通道的门控变量。 , , , ,和 分别代表快速钠电流,钾电流,持续钠电流,漏电流和方波电流。C是膜电容。其中 为方波电流,是由三个变量所决定的, ,p是方波电流的周期,dc是方波电流的占空比,max是方波电流的最大强度,min是方波电流的最小强度,在本文中取电流最小强度min = 0。因此,方波电流的变化主要由电流的最大强度max、占空比和周期决定。电压相关的激活和失活稳态和时间常数如下:
各离子电流描述如下: , , , 。
其它参数详见附录表A1。
3. 主要研究结果
由于方波电流的控制变量有三个,即电流强度max (本文中min = 0)周期p和占空比dc。下文中我们分别研究这三个变量对pre-BötC神经元放电模式的影响。
3.1. 无外激励刺激时,神经元的动力学行为
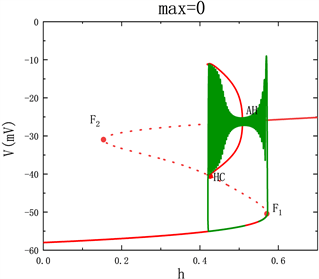
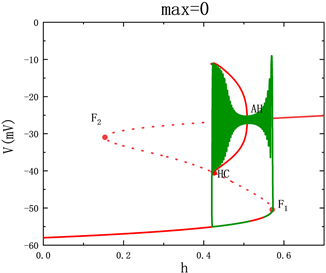
当外激励max = 0时,神经元的放电模式如图1(a)所示,对应的快子系统对慢变量h的分岔分析如图1(b)所示。其中,S型曲线中实线表示稳定平衡点,虚线表示不稳定平衡点。点F1和F2表示平衡点的鞍结分岔点,AH为Andronov-Hopf分岔。从AH分岔出的极限环(红色曲线)经过极限环的同宿轨分岔HC消失。系统轨线(绿色曲线)也叠加分岔图中。随着时间的演化,系统轨线(静息态)通过平衡点的鞍结分岔点F1时,跃迁到上支并围绕稳定焦点振荡。由于稳定焦点的吸引,轨线的振幅逐渐衰减,并穿过AH分岔点。由于稳定极限环的吸引,轨线的振幅逐渐增大,表现为振荡状态,最终振荡态经由同宿轨分岔HC落回到静息状态。所以这种簇放电模式为经由“fold/homoclinic”滞后环的“Hopf/homoclinic”簇放电。
 (a)
(a)
 (b)
(b)
Figure 1. Dynamic behavior of neurons without external excitation: (a) time series; (b) bifurcation diagram of fast subsystem
图1. 无外激励时神经元的动力学行为:(a) 时间序列;(b) 快子系统的分岔图
3.2. 电流强度对放电模式的影响
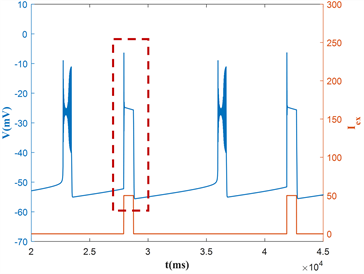
本节我们探讨外激励的强度对神经元的混合簇放电模式的影响,即通过电流强度最大值max的改变,来探究神经元的放电模式动力学变化。此时,固定周期 ( )和占空比dc = 6。当方波电流的最大强度max从0增加到50 mA时,诱导神经元产生的混合簇放电如图2(a)~(d)所示。随着电流强度最大值max的增大,使得混合簇放电中对应的簇内峰放电的振幅减小,即抑制了神经元的放电。
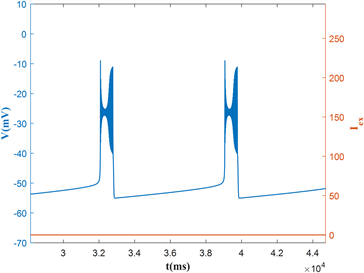 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
Figure 2. Effects of maximum current intensity max on firing activities: (a) max = 0; (b) max = 10; (c) max = 30; (d) max = 50
图2. 电流强度最大值max对神经元放电模式的影响:(a) max = 0;(b) max = 10;(c) max = 30;(d) max = 50
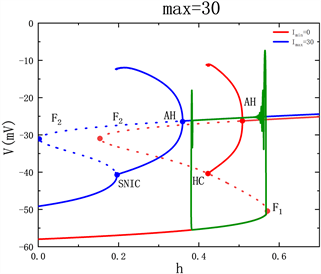
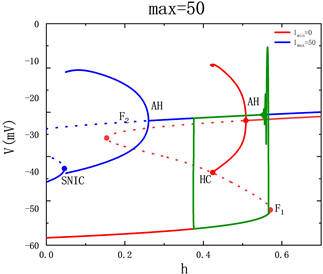
对应的快子系统对慢变参数h的分岔如图3所示,S型红色曲线表示max = 0时的分岔曲线,蓝色曲线表示对应的方波电流的最大强度max的分岔曲线,绿色曲线是在对应的方波电流作用下神经元的轨线,即混合簇放电中的第二个簇放电。
随着max的逐渐增加,高电流强度使得Hopf分岔点AH逐渐向左移动,从而使得稳定极限环也相应地向左移动,与低电流下的稳定极限环之间的距离逐渐增大,从而高电流的稳定极限环对神经元的放电产生的影响越来越小。当系统轨线通过低电流下的分岔点AH后,被吸引在高电流所对应的稳定焦点上。当max = 10时,如图3(b)所示,轨线通过高电流下的分岔点AH后,受稳定极限环的吸引发生振荡。当max = 30时,如图3(c)所示,轨线受稳定焦点的吸引以及Hopf分岔的慢通道滞后效应,不再发生振荡,即簇放电内的峰放电被抑制。
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
Figure 3. Bifurcation diagram of fast subsystem when the maximum current intensity max changed: (a) max = 0; (b) max = 10; (c) max = 30; (d) max = 50
图3. 电流强度最大值max变化时快子系统分岔图:(a) max = 0;(b) max = 10;(c) max = 30;(d) max = 50
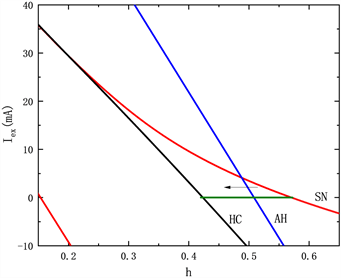
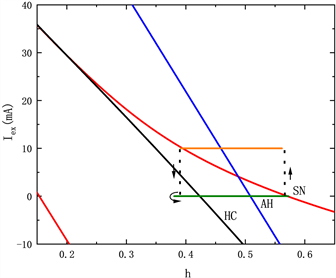
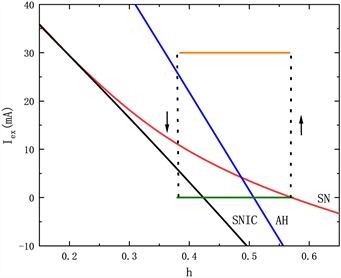
对应的快子系统的双参数分岔如图4所示,其中SN,AH,HC,SNIC分别表示平衡点的鞍结分岔(红色),Hopf 分岔(蓝色),同宿轨分岔(黑色)以及不变圆极限环的鞍结分岔(黑色)曲线。电流的最大值max
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
Figure 4. Two-parameter bifurcation diagram of fast subsystem when the maximum current intensity max changes: (a) max = 0; (b) max = 10; (c) max = 30; (d) max = 50
图4. 电流强度最大值max变化时快子系统双参数分岔图:(a) max = 0;(b) max = 10;(c) max = 30;(d) max = 50
曲线(橙色)和最小值min曲线(橄榄色)也叠加在(h, Iex)平面上。当电流max = 0时,即没有施加外激励作用时,双参数分岔如图4(a)所示,沿着h减小的方向,系统轨线到达SN点时跃迁到稳定焦点附近振荡,通过HC点后回到静息状态。当电流max = 10时,双参数分岔如图4(b)所示,沿着h减小的方向,高电流在到达HC之前跃迁到低电流的稳定极限环上振荡,随后回到静息状态,因此低电流在左侧有一个折返。如图4(c),图4(d)所示,当max = 30,max = 50时,沿着 减小的方向,系统轨线都是在高电流的SN点开始振荡,在到达SNIC之前回到静息状态。
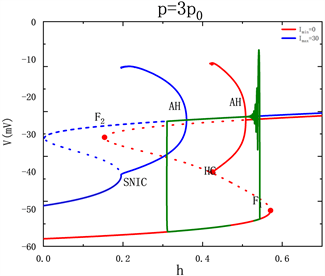
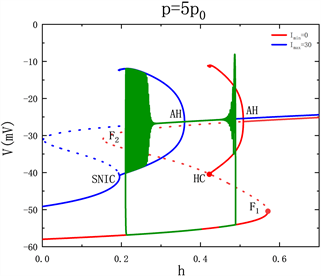
3.3. 周期p对放电模式的影响
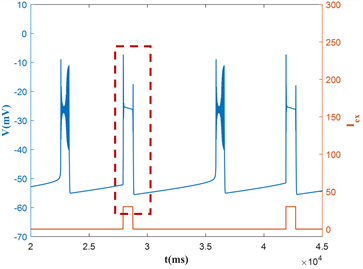
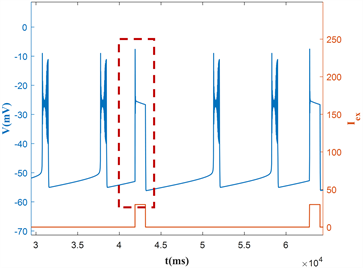
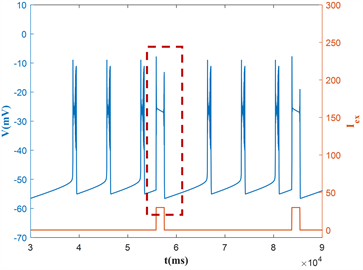
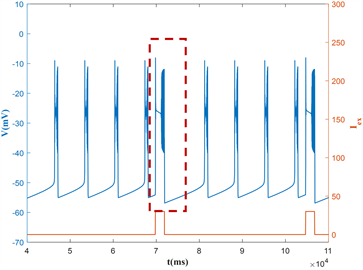
本节研究在具有不同周期p的方波电流激励下,神经元混合簇放电的模式改变。这里固定电流最大值max = 30,占空比dc = 6。由于混合簇放电的产生是由方波电流激励导致的,故方波电流的周期决定了混合簇的周期。随着方波电流的周期从2p0增加到5p0,混合簇放电中的胞体簇的个数也在有规律的增加,如图5所示,胞体簇放电的个数从1个增加到4个。
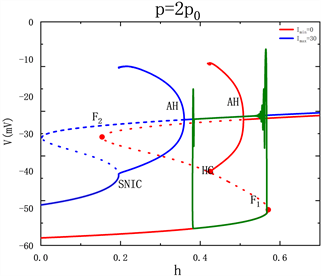
对应的快子系统对慢变参数h的分岔如图6(a)~(d)所示,随着周期p的增大,混合簇的轨迹本应该已经通过鞍结分岔点(F1)失去平衡状态,进而跳跃至上支的稳定焦点处。然而,由于高电流的突然介入,
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
Figure 5. Effect of period p on firing pattern of neurons ( ): (a) ; (b) ; (c) ; (d)
图5. 周期p对神经元放电模式的影响( ):(a) ;(b) ;(c) ;(d)
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
Figure 6. Bifurcation diagram of fast subsystem when period p changes: (a) ; (b) ; (c) ; (d)
图6. 周期p变化时快子系统分岔图:(a) ;(b) ;(c) ;(d)
系统轨迹在到达F1之前直接从低电流下的稳定平衡点曲线跳跃至上支,如图6(a),图6(b)所示。受高电流下的极限环的吸引,使得系统轨线在高电流的稳定极限环上振荡,如图6(c)所示。且随着周期的增大,轨线在高电流的稳定极限环上振荡的越久,如图6(d)所示。由于固定的占空比dc = 6的值很小,故当方波电流的周期按照倍数增大时,高电流持续时间的增长速度远远小于低电流持续时间的增长速度,且混合簇的产生是由方波电流作用决定的,因此体细胞簇的个数也会相应的增加。
对应的快子系统的双参数分岔如图7所示,此时高电流为max = 30。当 ,如图7(a)所示,系统轨线在鞍结分岔SN点处,沿着h减小的方向运动。系统轨线在到达AH点之前,在簇放电状态下从高电流跳到低电流,因此系统轨线必定在高电流的稳定焦点上振荡。随着周期p的增大,如图7(b)~(d)所示,即轨迹在低电流下成功到达SN,之后跳到高电流的分岔曲线上,因此在低电流下轨迹有一个折返。在静息状态下从低电流跳到高电流上,沿着h减小的方向运动,系统轨线在经过了AH曲线,且在到达SNIC曲线之前,从高电流跃迁到低电流上。因此,对应轨线在经过AH点后在高电流的分岔曲线上持续振荡,直至高电流不再作用于神经元上。
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
Figure 7. Two-parameter bifurcation diagram of the fast subsystem when the period p changes: (a) ; (b) ; (c) ; (d)
图7. 周期p变化时快子系统的双参数分岔图:(a) ;(b) ;(c) ;(d)
3.4. 占空比dc对放电模式的影响
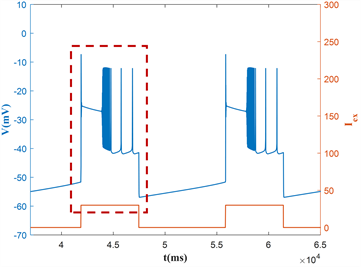
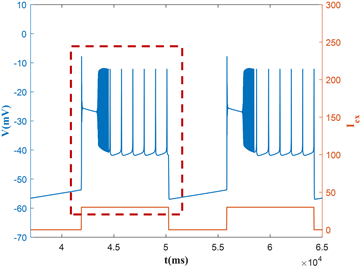
本节研究在不同占空比dc的方波电流激励下,混合簇放电的模式改变。这里固定电流最大值max = 30,周期 ( )。当占空比dc从30增加到60时,诱导神经元产生的混合簇放电如图8(a)~(d)所示。随着占空比dc的增大,混合簇的持续时间相应的增加。同时占空比dc越大,低电流的持续时间越短,混合簇放电的放电状态的时长越长。
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
Figure 8. Effect of duty cycle dc on firing mode of neurons: (a) dc = 30; (b) dc = 40; (c) dc = 50; (d) dc = 60
图8. 占空比dc对神经元放电模式的影响:(a) dc = 30;(b) dc = 40;(c) dc = 50;(d) dc = 60
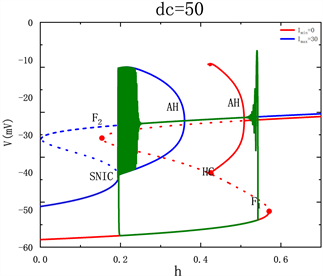
在快子系统的分岔图9(a)~(d)中,当占空比dc较小时,系统轨线(静息态)在分岔点F1处跳跃至上支的稳定焦点,并在高电流的稳定焦点附近振荡。随着占空比dc的增大,引起轨线(静息态)跳跃的节点提前,即在平衡点的鞍结分岔点F1的发生之前,如图9(a)~(d)所示。受高电流下的极限环的吸引,使得系统轨线在高电流的稳定极限环上振荡,最终经由高电流的不变圆上的鞍结分岔点(SNIC)跃迁到低电流的静息状态,故随着占空比dc的增大,神经元的两个混合簇放电之间的距离越来越小。
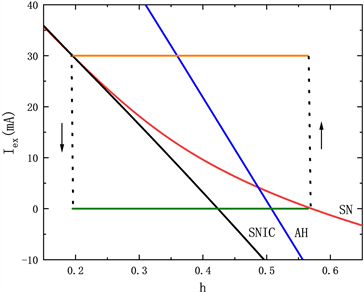
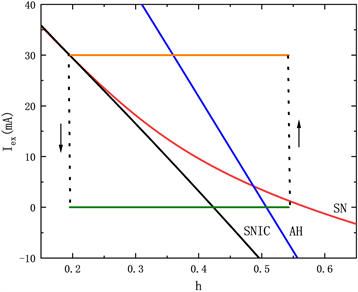
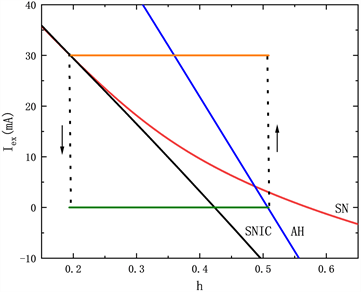
在快子系统的双参数分岔如图10(a)~(d)所示,此时电流最大值max = 30,周期 ( )。研究占空比dc。在高电流刺激结束时,系统轨线都是从高电流不变圆的鞍结分岔(SNIC)点跃迁到低电流上,回到静息状态。当dc = 30时,如图10(a)所示,轨迹在低电流下成功到达SN点之后,在AH点跳到高电流的分岔曲线上,因此在低电流下轨迹有一个折返。解释了在单参数分岔图9(a)中,系统轨线在F1点处跃迁到低电流的稳定焦点上,随后在通过AH点后,从低电流跳到高电流的稳定焦点上。随着占空比dc的增大,系统轨线从低电流跃迁到高电流的位置逐渐早于鞍结分岔并靠近AH点,如图10(b)~(d)所示。
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
Figure 9. Effects of duty cycle dc on the bifurcation structure of fast subsystem: (a) dc = 30; (b) dc = 40; (c) dc = 50; (d) dc = 60
图9. 占空比dc变化时快子系统分岔图:(a) dc = 30;(b) dc = 40;(c) dc = 50;(d) dc = 60
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
Figure 10. Two-parameter bifurcation diagram of fast subsystem when duty cycle dc changes: (a) dc = 30; (b) dc = 40; (c) dc = 50; (d) dc = 60
图10. 占空比dc变化时快子系统的双参数分岔图:(a) dc = 30;(b) dc = 40;(c) dc = 50;(d) dc = 60
4. 结论
本文选择了简单且易实现的方波电流作为外激励,运用单参数、双参数等动力学分析方法,分别研究方波电流的三个变量max,p,dc对神经元混合簇放电的影响。研究发现,随电流强度最大值max增大,混合簇放电中对应的簇内峰放电的振幅减小,即抑制了神经元的放电;混合簇的产生与方波电流的作用直接相关,方波电流的周期直接决定了混合簇的周期,当方波电流的周期p增大时,混合簇放电中对应的簇内峰放电周期增大;占空比dc增大,混合簇放电的持续时间相应的增加,同时占空比dc越大,低电流的持续时间越短,混合簇放电的放电状态的时长越长。结果表明方波电流可以诱导神经元产生不同类型的混合簇放电。本文的研究结果为进一步理解神经系统中混合簇放电的产生机制提供了有益的参考。
文章引用
蒋亚璐,陈雪丽. 方波电流对混合簇放电的影响及其动力学分析
Influence of Square Wave Current on Mixed Bursting and Its Dynamic Analysis[J]. 力学研究, 2023, 12(01): 56-67. https://doi.org/10.12677/IJM.2023.121006
参考文献
- 1. Pace, R.W., Mackay, D.D., Feldman, J.L., et al. (2007) Inspiratory Bursts in the Pre-Bötzinger Complex Depend on a Calcium-Activated Non-Specific Cation Current Linked to Glutamate Receptors in Neonatal Mice. The Journal of Physiology, 582, 113-125. https://doi.org/10.1113/jphysiol.2007.133660
- 2. Izhikevich, E.M. (2000) Neural Excitability, Spiking and Bursting. International Journal of Bifurcation and Chaos, 10, 1171-1266. https://doi.org/10.1142/S0218127400000840
- 3. Stojilkovic, S.S., Zemkova, H. and Van Goor, F. (2005) Biophysical Basis of Pituitary Cell Type-Specific 〖ca〗^(2+)Signaling-Secretion Coupling. Trends in Endocrinology & Metabolism, 16, 152-159. https://doi.org/10.1016/j.tem.2005.03.003
- 4. Smith, J.C., Ellenberger, H.H., Ballanyi, K., Richter, D.W. and Feldman, J.L. (1991) Pre-Bötzinger Complex: A Brainstem Region That May Generate Respiratory Rhythm in Mammals. Science, 254, 726-729. https://doi.org/10.1126/science.1683005
- 5. Lieske, S.P., Thoby-Brisson, M., Telgkamp, P., et al. (2000) Reconfiguration of the Neural Network Controlling Multiple Breathing Patterns: Eupnea, Sighs and Gasps. Nature Neuroscience, 3, 600-607. https://doi.org/10.1038/75776
- 6. Ding, X. and Li, Y. (2016) Period-Adding Bifurcation of Neural Firings Induced by Inhibitory Autapses with Time-Delay. Acta Physica Sinica, 65, 210502.
- 7. Butera, R.J., Rinzel, J. and Smith, J.C. (1999) Models of Respiratory Rhythm Generation in the Pre-Bötzinger Complex. I. Bursting Pacemaker Neurons. Journal of Neurophysiology, 82, 382-397. https://doi.org/10.1152/jn.1999.82.1.382
- 8. Butera, R.J., John, R. and Smith, J.C. (1999) Models of Respiratory Rhythm Generation in the Pre-Bötzinger Complex. II. Populations of Coupled Pacemaker Neurons. Journal of Neurophysiology, 82, 398-415. https://doi.org/10.1152/jn.1999.82.1.398
- 9. Rubin, J.E., Hayes, J.A., Mendenhall, J.L., et al. (2009) Calcium-Activated Nonspecific Cation Current and Synaptic Depression Promote Network-Dependent Burst Oscillations. Proceedings of the National Academy of Sciences, 106, 2939-2944. https://doi.org/10.1073/pnas.0808776106
- 10. Lü, Z., Liu, M. and Duan, L. (2021) Dynamical Analysis of Dendritic Mixed Bursting within the Pre-Bötzinger Complex. Nonlinear Dynamics, 103, 897-912. https://doi.org/10.1007/s11071-020-06097-1
- 11. Wang, Y.Y. and Rubin, J.E. (2017) Timescales and Mechanisms of Sigh-Like Bursting and Spiking in Models of Rhythmic Respiratory Neurons. The Journal of Mathematical Neuroscience, 7, Article No. 3. https://doi.org/10.1186/s13408-017-0045-5
- 12. Ji, W., Liu, M. and Duan, L. (2021) Influence of Electric Current and Magnetic Flow on Firing Patterns of Pre-Bötzinger Complex Model. Neural Plasticity, 2021, Article ID: 6655933. https://doi.org/10.1155/2021/6655933
- 13. Duan, L., Liang, T., Zhao, Y. and Xi, H. (2021) Multi-Time Scale Dynamics of Mixed Depolarization Block Bursting. Nonlinear Dynamics, 103, 1043-1053. https://doi.org/10.1007/s11071-020-05744-x
- 14. Wang, Y. and Rubin, J.E. (2016) Multiple Timescale Mixed Bursting Dynamics in a Respiratory Neuron Model. Journal of Computational Neuroscience, 41, 245-268. https://doi.org/10.1007/s10827-016-0616-6
- 15. Lü, Z., Chen, L. and Duan, L. (2019) Bifurcation Analysis of Mixed Bursting in the Pre-Bötzinger Complex. Applied Mathematical Modelling, 67, 234-251.
- 16. Park, C. and Rubin, J.E. (2013) Cooperation of Intrinsic Bursting and Calcium Oscillations Underlying Activity Patterns of Model Pre-Bötzinger Complex Neurons. Journal of Computational Neuroscience, 34, 345-366. https://doi.org/10.1007/s10827-012-0425-5
附录
Table A1. Parameter values in the theoretical model
表A1. 模型中的参数值
