Journal of Image and Signal Processing
Vol.
09
No.
01
(
2020
), Article ID:
33699
,
10
pages
10.12677/JISP.2020.91006
A Novel Image Encryption Algorithm Based on Chaotic Map
Jing Zhang, Ruisong Ye
Department of Mathematics, Shantou University, Shantou Guangdong

Received: Dec. 6th, 2019; accepted: Dec. 23rd, 2019; published: Dec. 30th, 2019

ABSTRACT
This paper presents a digital image encryption and decryption algorithm based on bit-planes and improved one-dimensional chaotic maps. Firstly, a simple and efficient new chaotic map is constructed by using two existing one-dimensional chaotic maps to generate random sequences for scrambling and diffusing the original image. Secondly, the original plain-image is decomposed into 8-bit planes, and the generated chaotic sequence is used to change the positions and values of the pixels to achieve the effect of scrambling and diffusion. Finally, the decomposed image is merged into gray image with 256 grayscales, and then the encrypted image is obtained by block shuffling operation. Experimental results show that the algorithm has good robustness and security. It can resist various attacks as well.
Keywords:Image Encryption, Chaotic Map, Bit-Plane

一种新的基于混沌映射的图像加密算法
张静,叶瑞松
汕头大学数学系,广东 汕头

收稿日期:2019年12月6日;录用日期:2019年12月23日;发布日期:2019年12月30日

摘 要
本文提出了一种基于比特位和改进的一维混沌映射的数字图像加解密算法。首先,使用两个存在的一维混沌映射构造了一个简单高效的新的混沌映射来产生随机序列,用于原始图像的置乱与扩散中。其次,将原始明文图像分解为8个位平面,将生成的混沌序列去改变像素值的位置和值,达到置乱和扩散的效果。最后,将分解后的图像合并成256个灰度级的灰度图像,再进一步进行分块的置乱操作,得到加密后的图像。实验结果表明,该算法具有良好的鲁棒性和安全性,可以抵抗各种攻击。
关键词 :图像加密,混沌映射,比特位平面

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着网络技术的高速发展,许多数字内容被传输和保存,个人的信息安全也变得越来越重要。在很多网络交流过程中我们常把数字图像作为传输的媒体,但随着通信设备的快速发展,一些不法分子通过不同渠道非法获取信息越来越容易,因此如何保证图像在传输过程中的安全性已成为近年来的一个重要研究课题,而图像加密是确保图像安全性的最有效方法之一 [1]。
当前,我们常用的图像加密技术主要是利用混沌系统来实现的。这是因为混沌系统的一些独特的性能适合用来进行图像加密,如对初始值和参数具有较强的敏感性、长期演化的不可预测性、易产生伪随机序列等特点,在很多图像加密系统中得到了广泛的应用 [2] [3] [4]。而一般的混沌加密系统可分为两部分,一部分是用来生成安全密码的混沌系统;另一部分是实现加密用的算法。用来生成密码的混沌系统可被分为两大类,既一维混沌系统和多维混沌系统。其中,多维混沌系统因具有的参数多,且它的结构复杂,故常常被使用,但存在着一些像软件实现困难及时间消耗大等的缺点。相反的,一维混沌系统的结构就比较简单,也易于实现,而且有较低的时间消耗。但是同样也有一些缺点,如,混沌区间是受限的,输出的混沌序列值分布不均匀等。因此,提出一个具有更好的混沌性能的混沌系统很有意义 [5]。在本文中,我们对两个存在的子混沌系统进行了改进,使改进的混沌系统有更大的混沌区间,更好的混沌性能。
近年来,基于位平面的图像加密算法因其独特的优点而被广泛研究。相比较像素级的置乱,基于位平面的置乱算法不仅可以改变像素的位置,也可以改变像素的值,所以有更好的加密效果 [6]。文献 [7] 提出了一种新的比特级加密算法,提出了基于反馈的扩散机制和自适应的置乱方法,确保了明文图像的微小变化能影响整个密文序列的变化。在文献 [8] 中,提出了一种比特级置乱和像素值共同置乱的方法去加强整个密码系统的安全性。文献 [9] 中明文图像被分解成了一个三维的比特矩阵,并用选择算法去打乱高4位的比特值,低4位不做改变。因为图像中的高4位包含了整个图像94.118%的信息,而低4位只占全部图像信息的5.882%。然而,这些基于比特位平面的图像加密算法由于位平面的分解而要进行多次的混沌迭代,会造成大量的时间消耗。因此,减少位平面加密算法的时间消耗也变得越来越重要。
此外,图像加密的安全性也是很重要的一项性能,但在众多的图像密码系统中,一些基于混沌的图像密码系统易受到各种攻击,即使连Fridrich在 [10] 中提出的混沌数字图像密码系统也未能幸免。主要原因是用于加密图像的密码仅与密钥有关,而与明文无关,因此它们易受选择明文攻击或已知明文攻击 [11]。基于上面提到的问题,本文提出了一种明文关联的混沌数字图像密码系统,其用于加密明文图像的密钥流不仅与密钥有关,而且与明文有关。混沌系统是一种将Logistic和Sine映射混合起来加以改进的动力系统。仿真实验表明该混沌系统具有很好的混沌特性。其遍历性和李亚普诺夫指数均比Logistic和Sine映射优越,系统的混沌控制参数空间大大提高。数值实验结果显示加密算法具有很好的安全性和加密性能,加密算法能抵抗各种类型攻击,包括统计分析、差分分析、选择明文、已知明文等。本文的组织结构如下。第二部分简单回顾使用的两个一维混沌映射,Logistic映射和Sine映射,并由这两个基本的混沌映射构造出新的混沌映射,分析其混沌行为。第三部分提出一种明文相关的置乱–扩散加密算法。第四部分进行仿真测试,得出结果并进行分析。第五部分为本文的结论。
2. 新的混沌系统
这一小节主要介绍两个一维混沌映射以及组合成的新的混沌映射,其中Logistic映射和Sine映射,是被广泛用到图像加密中的两种映射,这里使用它们来构造了一个新的混沌映射。
2.1. Logistic映射
Logistic映射是一种简单的非线性混沌方程,因其具有良好的混沌特性,常被拿来用在混沌图像加密的算法中。它的定义如下 [12]。
(1)
其中,u是一个控制参数,为了能保证输出的混沌序列的值在[0,1]内,它的取值范围确定为 ,并
随着u的不断变化,方程会显示出不同的动力学行为。 是输出的混沌序列。
2.2. Sine映射
Sine映射和Logistic映射有着相同的混沌行为,也是常见的一种简单的混沌系统,它的定义可以用下式描述。
(2)
r是它的控制参数,取值范围是 , 是输出的混沌序列。对于这两个基本的混沌系统,我们可通过查看它们的分岔图和李雅普诺夫图来观察它们的混沌行为。
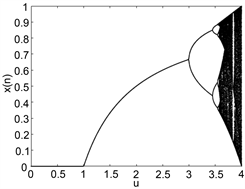
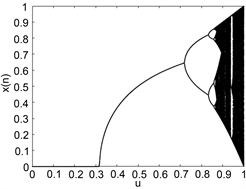
图1(a)和图2(a)分别是Logistic映射的分岔图和李雅普诺夫图,我们可看到,它仅在[3.57,4]这一区间内出现混沌行为,而且并不是里面的所有参数都有混沌行为,说明它的混沌区间是有限制的。在李亚普诺夫图中,出现正数说明该混沌映射有好的混沌性能,这里当 时,Logistic映射才有混沌行为。另外,我们还可以从图1(a)中看出Logistic映射输出的混沌序列中点的分布很不均匀,因此可以进一步改进它。图1(b),图2(b)分别是Sine映射的分岔图和李雅普诺夫图,它与Logistic映射有相同的混沌行为,都有混沌区间受限,点的分布不均匀等问题。
 (a)
(a)
 (b)
(b)
 (c)
(c)
Figure 1. Bifurcation graph. (a) Logistic mapping; (b) Sine mapping; (c) New chaotic mapping
图1. 分岔图。(a) Logistic映射;(b) Sine映射;(c) 新混沌映射
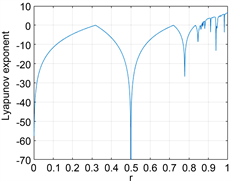
Figure 2. Lyapunov diagram. (a) Logistic mapping; (b) Sine mapping; (c) New chaotic mapping
图2. 李雅普诺夫图。(a) Logistic映射;(b) Sine映射;(c) 新混沌映射
2.3. 构造新的混沌映射
使用提出的新的混沌系统可解决一维混沌映射混沌区间受限及点的分布不均匀的问题。新的混沌系统的定义如下:
(3)
r是一个常数,这里我们取值为20,u是一个区间不受限制的控制参数,k的取值为18。图1(c),图2(c)分别是它的分岔图和李雅普诺夫图。从图中我们可以看出,相比于另两个混沌映射,它的混沌性能更好,点的分布更均匀。
3. 图像加密算法
3.1. 混沌系统初始值
在整个的加密过程中,使用了一个长为256哈希密钥,它是由SHA-256哈希函数生成的,并将这256位长的密钥以8位为一组分为32块。如 ,其中 , 用K和另给的4个外部密钥可得到混沌系统的初始值。如式(4)~(7)
(4)
(5)
(6)
(7)
从以上式子中,我们可得到一个取决于明文图像哈希值的混沌映射的初始值,这样做的好处是可以提高图像的明文敏感性。即使两幅明文图像仅有一个比特的值是不一样的,得到的哈希值却是完全不同的。
3.2. 图像加密算法
这部分采用如图3所示的置乱–扩散结构的加密算法。我们先将一幅灰度明文图像进行比特位分解,然后进行比特级置乱和扩散,为加强整个加密算法的效果,最后提出了一个块像素级置乱方案,进一步提升了整个算法的安全性。

Figure 3. Algorithm structure diagram
图3. 算法结构图
具体的操作步骤如下:
步骤1. 将大小为M × N的图像P由比特位平面分解(BBD)成大小为bt的图像PD,bt = M × 8N。
步骤2. 将x,r,u作为混沌映射的初始值代入式(3)中迭代 次,并舍弃前 次得新的长为bt的混沌序列 。
步骤3. 通过对生成的混沌序列S按从小到大进行排序,得到新的序列 和一个位置索引序列 ,使用位置索引置乱分解后的图像PD得到新的图像AP,置乱方法如(8)所示。
(8)
步骤4. 再将y,r,u作为混沌系统新的初始值,同样迭代 次获得长为bt的序列XS,进行(9)~(11)的操作,得到扩散后的图像C。
if ; (9)
if ; (10)
if (11)
步骤5. 将矩阵C进行比特位合并得M × N的图像CE。
步骤6. 对上面步骤中生成的序列S和XS分别进行(12)和(13)的计算。
(12)
(13)
步骤7. 将 和Xt相加,组合成长为16的数组bs:
, (14)
步骤8. 将bs按升序的方式进行排列,从而可得一个新的位置索引序列
(15)
步骤9. 把图像CE分割成16个小块,根据序列Tb打乱这些子块,得到最终的密文图像E。
图像的解密过程是加密过程的反向操作,可以无失真地还原原始的明文图像。
4. 实验结果和分析
为了估计算法的性能,使用的是标准的512 × 512的Lena图像,混沌系统的初始值 ,,参数 ,,,加密结果和解密结果如图4所示。
 (a)
(a)
 (b)
(b)
 (c)
(c)
Figure 4. Encryption and decryption diagram of the image
图4. 图像的加解密图
4.1. 密钥空间
为了图像加密的安全性,图像密码系统的密钥空间应该足够大,从而可以有效地抵抗穷举攻击。在我们提出的密码系统中,包括的密钥有256位的哈希值,混沌系统的初始值 ,,,,迭代次数 ,如果计算机的精度是10−14,提出的混沌系统的密钥空间是10108,远大于要求的20100。
4.2. 直方图分析
图像的直方图反映了一幅图像中的像素值的分布情况。一个安全的加密方案应使加密后的图像的直方图是均匀的才可以抵制任何统计攻击。在图5中给出了明文图像和密文图像的直方图,可以清晰的看到密文图像的像素值分布均匀,而明文图像的直方图跌宕起伏,所以加密后很好的隐藏了明文图像信息。
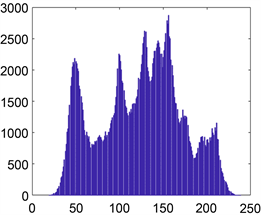 (a) 明文图像直方图
(a) 明文图像直方图
 (b) 密文图像直方图
(b) 密文图像直方图
Figure 5. Histogram analysis
图5. 直方图分析
4.3. 相关性分析
明文图像相邻像素间的高相关性是加密后的密文图像应该克服的缺点,所以要求加密后的密文图像的相关性应小于0.1,为了测试提出的加密方案中相邻像素的相关性,我们从明文图像和加密后的密文图像中随机选取了1000对相邻的像素值,利用公式(16)~(18)进行了相关性的计算。从图6中可看出,明文图像在水平,垂直,对角上的相邻像素点均具有较强的相关性,而密文图像中的相邻像素点没有相关性。表1是加密前后相邻像素值的相关系数。
(16)
(17)
, (18)
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
 (e)
(e)
 (f)
(f)
Figure 6. Correlation between adjacent pixels of plaintext image and ciphertext image
图6. 明文图像和密文图像相邻像素相关性
Table 1. Correlation coefficient of adjacent pixels
表1. 相邻像素相关系数
4.4. 敏感性分析
4.4.1. 密钥敏感性分析
为了保证密码系统的安全性,一个好的密码系统应该对密钥有较强的敏感性。所谓的密钥敏感性是指当密钥发生微小变化后,让其加密相同的明文图像后得到的密文图像与原始密文图像之间的差别情况。如果这两个密文图像有明显的差别,则表明使用的密码系统的密钥敏感性强。若两个密文图像的差别很小,则认为密钥敏感性差。我们以明文图像Lena为例,图7(a)是正确密钥解密出的图像。在这里,我们将原始密钥 改为 ,其它密钥保持不变,采用新密钥解密明文得到的解密图像,如图7(b)所示。同样的,让 ,其它密钥不变,解密出的图像为图7(c)所示,让 ,解密出的图像如图7(d)所示。对比发现微小改变密钥不能解密出图像,因此,它具有很好的密钥敏感性。

 (a) 正确密钥 (b) 改变x0的值
(a) 正确密钥 (b) 改变x0的值
 (c) 改变y0的值 (d) 改变u0的值
(c) 改变y0的值 (d) 改变u0的值
Figure 7. Key sensitivity analysis
图7. 密钥敏感性分析
4.4.2. 明文敏感性分析
加密后的图像对明文越敏感,表明算法的性能越好,越能抵抗各种攻击 [4]。通过对明文图像做微小改变,如只将明文的一个像素值改变,然后比较改变后得到的密文图像与原来的密文图像间的差别。比较的方法是使用NPCR (像素数改变率)和UACI (平均改变强度)这两个定性变量。它们的表示方法如式(19)~(21)。
(19)
(20)
其中 的定义如下
(21)
M,N是图像的大小, 和 是加密后的两个密文图像,它们只在一个像素点处的灰度值是不同的。通过随机选取明文图像中的像素值使其像素值加1,进行测试后,得出的NPCR和UACI的值分别是99.6091%和33.4579%,从中可以看出,提出的算法具有较好的明文敏感性。
4.5. 信息熵
信息熵是另一种反映图像信息不确定性的一种测试标准,灰度值的分布越均匀,信息熵越大,不确定性也就越大.计算公式如(22)所示:
(22)
其中L = 256,P(i)表示灰度值i出现的概率。一幅L = 256个灰度级的灰度图像,其信息熵最大值8在图像是完全均匀分布的随机图像时达到。一幅图像的信息熵越接近最大值,像素灰度值的分布越均匀。根据式(22)计算得到的明文图像Lena的信息熵仅为7.4434,而密文图像的信息熵结果达到7.9993,比已有的文献 [5] [13] 加密后得到的密文图像的信息熵结果更好,更接近最大值8,如表2所示。实验结果表明加密后的图像的灰度值分布均匀,有很好的信息熵。
Table 2. Information entropy
表2. 信息熵
5. 总结
在这篇文章中,我们利用改进后的混沌系统来进行图像加密。在密码系统中,我们首先将明文图像进行比特位分解,接着进行比特级置乱和扩散后,经过比特级合并,得到新的图像有效的打乱了原始图像的相关性,使其具有随机性。最后再进行了一次像素级的块置乱算法得到最终的密文图像。整个密码系统在进行一轮加密后就能获得良好的加密效果。实验结果表明,提出的加密算法能够抵抗各种攻击。
文章引用
张 静,叶瑞松. 一种新的基于混沌映射的图像加密算法
A Novel Image Encryption Algorithm Based on Chaotic Map[J]. 图像与信号处理, 2020, 09(01): 47-56. https://doi.org/10.12677/JISP.2020.91006
参考文献
- 1. 张勇. 混沌数字图像加密[M]. 北京: 清华大学出版社, 2016.
- 2. 徐超, 张雪锋. 改进的基于位平面的图像加密算法[J]. 计算机工程与设计, 2014, 35(2): 451-456.
- 3. Zhou, Y., Bao, L. and Chen, C.L.P. (2014) A New 1D Chaotic System for Image Encryption. Signal Processing, 97, 172-182.
https://doi.org/10.1016/j.sigpro.2013.10.034 - 4. Hua, Z., Zhou, Y., Pun, C.M., et al. (2015) 2D Sine Logistic Modulation Map for Image Encryption. Information Sciences, 297, 80-94.
https://doi.org/10.1016/j.ins.2014.11.018 - 5. Cao, C., Sun, K. and Liu, W. (2017) A Novel Bit-Level Image Encryption Algorithm Based on 2D-LICM Hyperchaotic Map. Signal Processing, 143, 122-133.
https://doi.org/10.1016/j.sigpro.2017.08.020 - 6. Xu, L., Li, Z., Li, J., et al. (2016) A Novel Bit-Level Image Encryption Algorithm Based on Chaotic Maps. Optics and Lasers in Engineering, 78, 17-25.
https://doi.org/10.1016/j.optlaseng.2015.09.007 - 7. Liu, D.D., Zhang, W., Yu, H., et al. (2018) An Image Encryption Scheme Using Self-Adaptive Selective Permutation and Inter-Intra-Block Feedback Diffusion. Signal Processing, 151, 130-143.
https://doi.org/10.1016/j.sigpro.2018.05.008 - 8. Li, Y., Wang, C. and Chen, H. (2017) A Hyper-Chaos-Based Image Encryption Algorithm Using Pixel-Level Permutation and Bit-Level Permutation. Optics & Lasers in Engineering, 90, 238-246.
https://doi.org/10.1016/j.optlaseng.2016.10.020 - 9. Liu, J., Yang, D., Zhou, H., et al. (2018) A Digital Image Encryption Algorithm Based on Bit-Planes and an Improved Logistic Map. Multimedia Tools & Applications, 77, 10217-10233.
https://doi.org/10.1007/s11042-017-5406-2 - 10. Fridrich, J. (1998) Symmetric Ciphers Based on Two-Dimensional Chaotic Maps. International Journal of Bifurcation and Chaos, 8, 1259-1284.
https://doi.org/10.1142/S021812749800098X - 11. Jolfaei, A., Wu, X.W. and Muthukkumarasamy, V. (2014) Comments on the Security of “Diffusion-Substitution Based Gray Image Encryption” Scheme. Digital Signal Processing, 32, 34-36.
https://doi.org/10.1016/j.dsp.2014.05.011 - 12. Phatak, S.C. and Rao, S.S. (1995) Logistic Map: A Possible Random-Number Generator. Physical Review, 51, 3670-3678.
https://doi.org/10.1103/PhysRevE.51.3670 - 13. Chen, J.X., Zhu, Z.L., Fu, C., et al. (2015) An Efficient Image Encryption Scheme Using Gray Code Based Permutation Approach. Optics and Lasers in Engineering, 67, 191-204.
https://doi.org/10.1016/j.optlaseng.2014.11.017
