Software Engineering and Applications
Vol.
09
No.
01
(
2020
), Article ID:
34178
,
7
pages
10.12677/SEA.2020.91006
A Decision Procedure of EUF Formulas Based on Eager Encoding
Mengqi Cheng, Siran Lei, Jianguo Jiang
School of Mathematics, Liaoning Normal University, Dalian Liaoning

Received: Jan. 23rd, 2020; accepted: Feb. 6th, 2020; published: Feb. 13th, 2020

ABSTRACT
In the formal verification community, a decision procedure of EUF formulas based on eager encoding method has practical advantages in solving certain problems. It also promotes the option of deciding a combination of theories by reducing them to this logic. In this paper, in order to find an efficient decision procedure of EUF formulas based on eager encoding, an eager approach is studied that an EUF formula is reduced to propositional logic formula by Ackermann’s method and an algorithm based on a nonpolar equality graph. The DPLIB library written in C++ language is provided for simplifying the development of the procedure. After adding the code to implement the above algorithms and compiling it on Linux system, it can be called to solve an EUF formula faster.
Keywords:EUF Formula, Ackermann’s Reduction, Equality Graph

基于活性编码的EUF公式的判定过程
程梦奇,雷斯然,江建国
辽宁师范大学数学学院,辽宁 大连

收稿日期:2020年1月23日;录用日期:2020年2月6日;发布日期:2020年2月13日

摘 要
在形式化验证领域,EUF公式的活性编码判定过程解决某些问题具有实际的优势,判定组合理论时,该方法选择将其归约为命题公式,更易于求解。本文以寻找高效的EUF公式的活性编码判定过程为目的,研究了一个活性编码方法,即通过Ackermann归约算法以及基于非极性等式图的归约算法,将EUF公式归约为等可满足性的命题公式。为了简化这一方法的实现进程,本文基于C++语言编写的DPLIB库,根据上述算法添加程序并成功编译于Linux系统,可以调用它更快的求解EUF公式。
关键词 :EUF公式,Ackermann归约,等式图

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在形式化验证领域,带未解释函数的等式逻辑公式(EUF)的判定过程得到了广泛的应用,很多实际问题可以建模成EUF公式的可满足性判定问题,例如:电路的等价性验证、程序的等价性验证、编译的转换有效性验证等 [1] [2] [3]。
到目前为止,针对EUF公式的可满足性求解问题,它的判定过程大体上分为两类:惰性编码(lazy encoding)和活性编码(eager encoding)。惰性编码判定过程是目前SMT领域内的主流方法,该方法基于SAT求解器与理论求解器之间的相互作用,并且理论求解器仅仅在需要时被引入,目的是检测理论文字集的可满足性。对EUF公式而言,该方法的主要思想是:首先找到满足公式命题结构的赋值,然后根据理论验证这些赋值。这种方法的缺点是,满足公式命题结构的赋值的数量在公式的大小上可能是指数级的,当理论求解器需要被调入时,可能会遇到瓶颈 [4] [5]。
基于活性编码判定EUF公式,可以避免遇到这种情况。因为它不依赖于SAT求解器和理论求解器的交替使用,而是将一个理论公式归约成一个等可满足性的命题公式,仅仅使用SAT求解器判定该命题公式的可满足性即可判定原始公式的可满足性。这个方法的好处在于,它可以充分地利用高效的SAT求解器,不用针对EUF理论去开发特定的理论求解器。
活性编码方法是早期SMT领域内的主要方法,主要包括:per-constraint方法 [6] 和small-domain instantiation方法 [7]。一个高效的将EUF公式归约为命题公式的方法,不仅能够提高其求解效率,还能够将它与命题逻辑级的其他理论整合在一起 [8] [9] [10]。该方法的求解效率依赖于EUF公式归约为命题公式的效率和SAT求解器自身的效率。因此寻找一个好的活性编码方法对EUF公式的求解至关重要。
为验证EUF公式的可满足性,本文给出了一种高效的活性编码判定方法,首先消去公式中的未解释函数,依靠函数的共同属性——函数一致性,在第二节主要介绍把判定EUF公式归约为判定等式公式的Ackermann归约算法,这个方法通过增加一些约束来加强函数一致性。然后消去公式中的等式谓词,依靠等式的传递性,在第三节提出基于非极性等式图将等式逻辑公式归约为命题逻辑公式的算法。最后,在DPLIB库1的基础上,添加实现上述算法的C++程序,并成功在Linux系统上编译,可以调用它更快的求解EUF公式。
2. Ackermann归约
本节研究的是将EUF公式归约为等可满足性的等式公式的方法。首先,通过一个例子简要介绍EUF公式, 是一个EUF公式,其中x和y是无限数域上的变量,F和G是未解释函数, 和 是原子公式。然后,给出EUF公式的语法定义。
定义 2.1. 带未解释函数的等式逻辑公式(EUF)的语法定义如下:
公式:公式Ù公式 | Ø公式 |(公式)| 原子
原子:项 = 项 | 谓词符号(项列表)
项:标识符 | 函数符号(项列表)
给定一个EUF公式,通常用 表示。其中,标识符是定义在一个无限数域上的变量。
为验证EUF公式的有效性,本文提到了Ackermann归约算法,该方法将判定该公式归约为判定等式逻辑公式,其中涉及一个重要的内容,即函数一致性规则:同一个函数的不同实例参数相等时,则返回相等的函数值 [11]。
为消去EUF公式中的未解释函数,Ackermann归约对公式添加了明确的约束,目的是加强函数一致性。该算法读到了一个EUF公式 ,验证该公式是否有效,下面把它转化为一个等式公式 ,如下所示:
(2.1)
其中, 是函数一致性约束的合取式, 是 的扁平化公式,公式中每一个函数实例用一个新变量来替换。
根据输入的公式做出一些假设:该公式只含有一个未解释函数且单参,并且不存在有相同参数值的两个函数实例。然后,给出简化的Ackermann归约算法。

例 2.2. 考虑公式,
(2.2)
使用算法2.1将该公式归约为等式公式。
观察该公式,假设从左到右依次找到关于F的函数实例,并且将索引赋给它们,根据这个步骤可以计算出 和 ,如下:
(2.3)
(2.4)
当且仅当等式公式(2.1) 有效,原始EUF公式(2.2)是有效的。
对于更为复杂的EUF公式而言,如何通过Ackermann归约算法将它们归约为等式公式,接下来给出两个例子,展示该算法的扩展应用过程:
例 2.3. 给定公式:
(2.5)
用对应的项变量替换每一个函数实例,计算出 :
(2.6)
计算出函数一致性约束的合取式,即:
(2.7)
最后,等式公式为 ,接下来验证它的有效性。
上面这个例子展示了,对于多参数函数如何来扩展这个归约法:仅当一对函数实例的所有参数都成对相等时,返回相等的函数值。
事实上读者可以观察到这些约束中的大多数是多余的,公式的有效性仅仅取决于 与 ,和 与 这两对函数实例是相等的。因此,在(2.7)式中,只有第二个和第五个约束是必要的。实践中,这样的观察是有必要的,因为函数一致性约束的数量以平方式增长可能会成为一个瓶颈。在这种情况下,通常是在检测公式的有效性之前检测出能够在多项式时间内被移除的比较大的约束集,这种方法的更多细节参考文献 [12]。
例 2.4. 检测公式的有效性:
(2.8)
由内而外将索引赋给函数实例,计算得:
(2.9)
(2.10)
最后,得:
(2.11)
从这个例子可以很清晰地看出,如何将Ackermann归约算法推广应用于多重未解释函数。
假设已经用Ackermann归约方法消去公式中的未解释函数,得到了一个等式公式。接下来,提出一个基于非极性等式图将等式逻辑公式归约到命题逻辑公式的方法。
3. 基于非极性等式图的归约
假设给出的等式公式是没有常量的否定范式(NNF),记为 , 表示 的原子集。
定义 3.1. 给定一个等式公式 ,存在对应 的非极性等式图,是一个无向图 ,其中V中的节点对应 中的变量,E中的边对应 中的等式谓词 ,用 表示。
非极性等式图是等式图的一个退化版本,因为它忽略了等式谓词的极性 [13] [14]。等式公式基于图方法归约到命题公式是由Bryant和Velev提出的一个判定过程 [15]。
给定一个等式公式 ,由该公式产生两个命题公式 和 ,
是可满足的 是可满足的。(3.1)
和 定义如下:
1) 是 的命题架, 中形如 的每个等式谓词由一个新的布尔变量 来替换。举例,
(3.2)
编码,得
(3.3)
由此可见,如果 是可满足的,那么 是可满足的。然而,其它情况是不成立的,比如在上述示例中,虽然公式(3.2)是不可满足的,但是它的编码(3.3)是可满足的,这是因为在编码过程中丢失了等式关系的传递。为了保持等可满足性,则需要添加一些约束,即 。
2) 是一个蕴含合取式,被称为传递约束。每个蕴含合取式都与非极性等式图中的一个回路相关,一个具有n个边的回路,当其中 个边被赋值为TRUE时, 禁止赋值FALSE给剩余的那个边。给每个回路中的每个边强加此约束是(3.1)成立的充分条件。
例 3.2. 在一个非极性等式图中,原子 形成了一个具有3个边的回路。下面的约束充分满足了公式(3.1)中等式关系的传递性:
(3.4)
然而,给每个回路增加n个约束并不实际,因为在一个给定的无向图上可能会存在指数式数量的回路。
定义 3.3. 回路中两个不相邻节点连成的边,被称为回路的弦。在给定的图中,一个没有弦的回路被称为无弦回路。
定理 3.4. 等式公式与编码后的命题公式等可满足性成立的充分条件是,在简单无弦回路上增加传递约束。
例 3.5. 考虑图1中的回路 ,该回路包含弦 ,因此,它不是无弦回路。假设赋TRUE给这个回路中除了 的所有边。如果 被赋值为TRUE,那么对简单无弦回路 的赋值与传递性冲突。如果 被赋值为FALSE,那么对简单无弦回路 的赋值与传递性冲突。因此,在无弦回路上的约束足够阻止赋给包含一个弦的回路违反传递性的值。
图中简单无弦回路的数量在顶点数量内仍然可以是指数式的。因此,构造 使其直接约束每个这样的回路在变量数量内都可以使这个公式的大小成为指数式的。有:
定义 3.6. 在一个给定的无向图中,只含有长度小于4的回路(无弦回路),称之为弦图。
每个图形可以在多项式时间内以顶点数构成,由于弦图中唯一的无弦回路是三角形,这表示将定理3.4应用于这样的图形会导致在变量数量内的公式大小不超过三次方(为图中的每个三角形构造三个约束)。

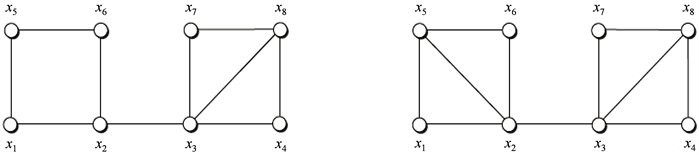
Figure 1. A nonchordal nonpolar equality graph corresponding to (left), and a possible chordor version of it (right)
图1. 左图是对应 的一个非极性无弦等式图,右图是它的一个可能的弦图
给定一个等式公式 ,算法3.1的第二步构造出了对应 的非极性等式图,若该图是一个无弦图,则在第三步添加新弦将其弦化,使其成为一个弦图,在这个过程中新添加的弦用出现在 但不在 里的新变量来表示。
例 3.7. 图1描绘了使其弦化之前和之后的非极性等式图,用实边表示。图形弦化后,它包含四个三角形,因此, 包含了12个约束。例如,三角形 ,它的约束条件是
(3.6)
图形弦化后,添加的弦用一个新的辅助变量 表示,出现在 里而不在 里。
4. 结论
本文针对EUF公式的可满足性求解问题,给出了一种可实现的活性编码判定过程。DPLIB库提供了部分基础程序,以简化该判定过程的开发。在这个基础上,添加有关活性编码算法的相关实现,并已于Linux系统中成功编译,加快了EUF公式的求解速度。但是本文中的两个算法中分别添加的函数一致性约束合取式与传递约束合取式的数量对求解效率可能有一定的阻碍,如何优化本文中的活性编码方法使其求解效率更高,还有待进一步地研究。
文章引用
程梦奇,雷斯然,江建国. 基于活性编码的EUF公式的判定过程
A Decision Procedure of EUF Formulas Based on Eager Encoding[J]. 软件工程与应用, 2020, 09(01): 49-55. https://doi.org/10.12677/SEA.2020.91006
参考文献
- 1. Kroening, D. and Strichman, O. (2016) Equality Logic and Uninterpreted Functions. In: Decision Procedures. Texts in Theoretical Computer Science. An EATCS Series, Springer, Berlin, 77-95.https://doi.org/10.1007/978-3-662-50497-0_4
- 2. Lei, B.U. and Bao, X.D. (2014) Formal Verification of Hybrid System. Journal of Software, 25, 219-233.
- 3. Bryant, R.E., German, S. and Velev, M.N. (2001) Processor Verification Using Efficient Reductions of the Logic of Uninterpreted Functions to Propositional Logic. ACM Transactions on Computational Logic, 2, 1-41.https://doi.org/10.1145/371282.371364
- 4. Ganzinger, H., Hagen, G., Nieuwenhuis, R., Oliveras, A. and Peled, D. (2004) DPLL(T): Fast Decision Procedures. In: Alur, R. and Peled, D.A., Eds., Computer Aided Verification. CAV 2004. Lecture Notes in Computer Science, Volume 3114, Springer, Berlin, Heidelberg, 175-188. https://doi.org/10.1007/978-3-540-27813-9_14
- 5. 金继伟, 马菲菲, 张健. SMT求解技术简述[J]. 计算机科学与探索, 2015, 9(7): 769-780.
- 6. Seshia, S.A., Lahiri, S.K. and Bryant, R.E. (2003) A Hybrid SAT-Based Decision Procedure for Separation Logic with Uninterpreted Functions. In: Proceedings of the 40th Annual Design Automation Conference, ACM, New York, 425-430. https://doi.org/10.1145/775832.775945
- 7. Pnueli, A., Rodeh, Y. and Shtrichman, O. (1999) Deciding Equality Formulas by Small Domains Instantiations. In: Halbwachs, N. and Peled, D., Eds., Computer Aided Verification. CAV 1999. Lecture Notes in Computer Science, Volume 1633, Springer, Berlin, Heidelberg, 455-469. https://doi.org/10.1007/3-540-48683-6_39
- 8. 王翀, 吕荫润, 陈力, 王秀利, 王永吉. SMT求解技术的发展及最新应用研究综述[J]. 计算机研究与发展, 2017, 54(7): 1405-1425.
- 9. Kroening, D. and Strichman, O. (2009) A Framework for Satisfiability Modulo Theories. Formal Aspects of Computing, 21, 485-494. https://doi.org/10.1007/s00165-009-0105-z
- 10. Strichman, O. (2002) On Solving Presburger and Linear Arithmetic with SAT. In: Aagaard, M.D. and O’Leary, J.W., Eds., Formal Methods in Computer-Aided Design. FMCAD 2002. Lecture Notes in Computer Science, Volume 2517, Springer, Berlin, Heidelberg, 160-170. https://doi.org/10.1007/3-540-36126-X_10
- 11. Bryant, R.E., German, S. and Velev, M.N. (1999) Exploiting Positive Equality in a Logic of Equality with Uninterpreted Functions. In: Halbwachs, N. and Peled, D., Eds., Computer Aided Verification. CAV 1999. Lecture Notes in Computer Science, Volume 1633, Springer, Berlin, Heidelberg, 470-482. https://doi.org/10.1007/3-540-48683-6_40
- 12. Pnueli, A. and Strichman, O. (2006) Reduced Functional Consistency of Uninterpreted Functions. Electronic Notes in Computer Science, 144, 53-65. https://doi.org/10.1016/j.entcs.2005.12.006
- 13. Rodeh, Y. and Shtrichman, O. (2001) Finite Instantiations in Equivalence Logic with Uninterpreted Functions. In: Berry, G., Comon, H. and Finkel, A., Eds., Computer Aided Verification. CAV 2001. Lecture Notes in Computer Science, Volume 2102. Springer, Berlin, Heidelberg, 144-154. https://doi.org/10.1007/3-540-44585-4_13
- 14. Rodeh, Y. and Strichman, O. (2006) Building Small Equality Graphs for Deciding Equality Logic with Uninterpreted Functions. Information and Computation, 204, 26-59. https://doi.org/10.1016/j.ic.2005.08.001
- 15. Bryant, R.E. and Velev, M.N. (2002) Boolean Satisfiability with Transitivity Constraints. ACM Transactions on Computational Logic, 3, 604-627. https://doi.org/10.1145/566385.566390
NOTES
1http://www.decision-procedures.org/