Dynamical Systems and Control
Vol.07 No.01(2018), Article ID:23583,8
pages
10.12677/DSC.2018.71006
A New Optimized Compensation Algorithm of Conic Error
Lijun Gu, Xiaoning Fu
School of Electromechanical Engineering, Xidian University, Xi’an Shaanxi

Received: Dec. 22nd, 2017; accepted: Jan. 8th, 2018; published: Jan. 29th, 2018

ABSTRACT
In order to solve the noncommutative error existing in the strap down inertial navigation system, this paper presents an improved coning error optimization algorithm to improve the solution accuracy. The algorithm optimizes the overlapped optimization algorithm further. Firstly, the error criterion of the classical coning motion is established; secondly, the optimized formula of the compensation algorithm is deduced and the optimal compensation coefficient is obtained; finally, the optimized algorithm under different coning motion environment is simulated. The results show that attitude calculation accuracy through improved algorithm is better than the traditional algorithm and overlapping algorithm; what’s more, the calculation accuracy of four-sample is better than the two-sample and three-sample.
Keywords:Strap-Down Inertial Navigation System, Equivalent Rotation Vector, Noncommutative Error, Compensation Coefficient
一种新的圆锥误差优化补偿算法
古丽军,付小宁
西安电子科技大学机电工程学院,陕西 西安
收稿日期:2017年12月22日;录用日期:2018年1月8日;发布日期:2018年1月29日

摘 要
为了解决捷联惯导系统中存在的不可交换误差的问题,本文提出了一种改进的圆锥误差优化算法来提高解算精度。该算法对重叠式圆锥误差优化算法进行了进一步优化。首先对经典圆锥运动建立误差准则,其次推导出优化的补偿算法的公式,给出了优化补偿系数,最后,在某一圆锥运动环境下对改进的算法进行仿真。结果表明,改进的算法得到的姿态解算精度与传统算法和重叠式算法相比,都得到了一定的提高,并且与二子样和三子样相比,四子样的解算精度效果最好。
关键词 :捷联惯导系统,等效旋转矢量,不可交换误差,补偿系数

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在捷联惯导系统中,姿态解算在整个惯性导航系统中是非常重要的 [1] 。在载体上固联着的导航系统,可以直接敏感载体的运动 [2] ,因此,姿态实时解算和更新是捷联惯导的尤为关键的技术之一。在载体运动过程中,刚体的有限转动会产生不可交换误差。锥运动是捷联惯导系统最恶劣的工作环境,这一不可交换误差作为整个姿态解算过程中的主要误差源,很多学者都用对这一误差优化的结果来评价一个姿态更新算法的优劣。由此可见,有效抑制圆锥误差对提高导航精度有显著的意义。
目前,大量国内外学者都对圆锥误差的优化算法这一领域进行了深入研究:等效旋转矢量的概念由外国学者Bortz和Jordon提出,这一概念的提出为之后研究的大量关于姿态更新的多子样算法提供了强有力的理论依据 [3] [4] ;秦永元等人在旋转矢量法的基础上,推导出了二子样到四子样等多子样算法的公式 [5] ;陈建锋等 [6] 提出一种基于角速率输入的进一步优化的补偿算法;丁杨斌通过已经得到的当前时刻之前的两个周期的姿态数据对结果进行优化修正 [7] ;肖胜从运动学角度给出了圆锥误差的诠释,提出了流水式旋转矢量姿态更新算法 [8] ;王真等主要针对三子样,提出了二次迭代优化算法 [9] ;杨浩天利用前两个计算周期陀螺输出的角增量信息和当前时刻陀螺采样值通过重叠式采样的方式进行圆锥误差补偿 [10] 。
目前研究出的的圆锥补偿算已经比较成熟,但是还存在一些问题,如在相同的采样频率下,增加子样数,会降低导航系统的姿态更新频率,但同时会增加导航计算机的计算量,给硬件造成一定的负担。
本文在抑制圆锥误差的传统算法的基础上,提出一种改进的补偿算法,即对重叠式采样算法的周期项进行优化,分别对二子样,三子样和四子样进行仿真,验证所提算法的正确性。
2. 圆锥运动与圆锥误差
圆锥效应是刚体运动中一种比较常见的现象。若某一载体作锥运动时,此时的不可交换误差所反映出的情况最为恶劣。
模拟载体角运动时,我们通常用锥运动来进行建模。用如下的单位矢量表示:
(1)
其中, , 为锥运动频率,半锥角 。
在我们所表示的经典圆锥运动的环境下,表示坐标系相对运动的姿态四元数 和角速率 通常可以用下列公式来表示:
(2)
(3)
3. 优化算法的误差准则
载体运动过程中的姿态四元数,通常以如下形式进行姿态更新
(4)
其中, 为 时刻的姿态四元数, 为 时刻的姿态四元数, 为这一时间间隔 内姿态四元数的变化量,可以由下式得到:
(5)
这个公式中, 为这一时间间隔 内旋转矢量的变化量,其大小为 。
在这一时间间隔 内,对Bortz方程积分并取近似,可以得到 的理想值 :
(6)
经典圆锥运动下, 可以表示为:
(7)
若将时间间隔 分为N个宽度,则可以得到N个角增量信号,传统圆锥算法以及改进的重叠式优化算法针对的都是非周期项,本文在此基础上,提出一种基于重叠式采样的二次优化算法。
假设旋转矢量的变化量为:
(8)
其中, , 为重叠式算法的优化系数, 为本文算法的优化补偿系数。
(9)
(10)
(11)
具体的二次优化的误差准则定义为:
(12)
将(9) (10) (11)代入(8),并将(7) (8)代入(12)得:
(13)
其中,
(14)
4. 确定优化算法的系数
当 时,式(8)是未进行优化的重叠式算法的表达式。对重叠式算法进行优化后的系数如表1所示。
本文所提出的新算法的补偿系数可以通过以下步骤来确定:
1) 将式(13)中的正弦函数全都展开成关于 的三角函数,并对同类项进行合并;
2) 令关于 的余弦函数项的系数为0,得到:
Table 1. Optimized coefficient of overlapping algorithm
表1. 重叠式算法的优化系数
(15)
3) 对下述公式中关于 的正弦函数项的系数X进行幂级数展开,即:
(16)
4) 对上述公式中的同类项进行合并,并且令与 有关且阶次不超过(2N − 3)的各项的系数均为0,即:
(17)
5) 根据式(15) (17)确定二次优化补偿系数 。
通过计算,将N = 2 − 4时的优化结果列于表2。
5. 仿真验证
假设某一载体运动的锥运动频率 ,半锥角 ,算法更新周期 ,仿真时间为 , 。
在这一运动环境下,对传统算法、重叠式优化算法以及本文所提出的优化算法的二子样(图1,图2)、三子样(图3,图4)、四子样(图5,图6)进行仿真,结果如图1~图6所示。
6. 结论
从图1~图6可以看出,传统算法随着子样数N的增加,姿态误差不仅没有提高,反而出现停滞甚至下降的趋势。本文所提出的算法和重叠式算法相比,对于二子样而言,两者的优化系数相同,因此两者的二子样的姿态误差相同,但比传统的算法误差要小很多。除了二子样外,三子样和四子样的仿真结果
Table 2. Optimized compensation coefficient of algorithm in this paper
表2. 本文算法的优化补偿系数
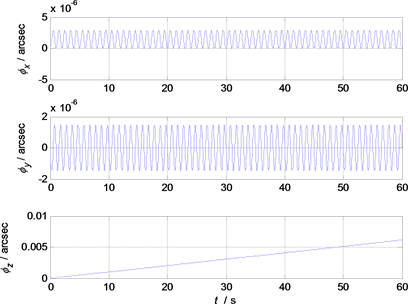
Figure 1. Traditional algorithm attitude error of the two-sample
图1. 传统的二子样算法姿态误差

Figure 2. Attitude error contrast of overlapping algorithm and algorithm of the two-sample in this paper
图2. 重叠式算法与本文算法的二子样姿态误差对比

Figure 3. Traditional algorithm attitude error of the three-sample
图3. 传统的三子样算法姿态误差

Figure 4. Attitude error contrast of overlapping algorithm and algorithm of the three-sample in this paper
图4. 重叠式算法与本文算法的三子样姿态误差对比

Figure 5. Traditional algorithm attitude error of the four-sample
图5. 传统的四子样算法姿态误差

Figure 6. Attitude error contrast of overlapping algorithm and algorithm of the four-sample in this paper
图6. 重叠式算法与本文算法的四子样姿态误差对比
都表明,本文所提出的算法要优于重叠式优化算法和传统算法,尤其是四子样算法,姿态误差比相应的传统算法和重叠式算法优化了1~2个数量级。
文章引用
古丽军,付小宁. 一种新的圆锥误差优化补偿算法
A New Optimized Compensation Algorithm of Conic Error[J]. 动力系统与控制, 2018, 07(01): 61-68. http://dx.doi.org/10.12677/DSC.2018.71006
参考文献 (References)
- 1. 李海涛, 曹咏弘, 祖静. 等效旋转矢量法在旋转弹姿态解算中的应用[J]. 测试技术学报, 2011, 25(4): 287-291.
- 2. 程承, 潘泉, 李汉舟. 一种新的捷联惯导系统圆锥误差补偿算法研究[J]. 弹箭与制导学报, 2014, 34(1): 1-4.
- 3. Bortz, J.E. (2007) A New Mathematical Formulation for Strapdown Inertial Navigation. IEEE Trans-actions on Aerospace & Electronic Systems, AES-7, 61-66.
https://doi.org/10.1109/TAES.1971.310252 - 4. Jordan, J.W. (1969) An Accurate Strapdown Direction Cosine Algorithm.
- 5. 秦永元, 张士邈. 捷联惯导姿态更新的四子样旋转矢量优化算法研究[J]. 中国惯性技术学报, 2001, 9(4): 1-7.
- 6. 陈建锋, 陈熙源, 祝雪芬. 一种基于二次优化的改进圆锥算法[J]. 中国惯性技术学报, 2012, 20(2): 131-135.
- 7. 丁杨斌, 满顺强, 申功勋. 一种新的捷联惯导系统圆锥误差补偿算法[J]. 北京航空航天大学学报, 2007, 33(11): 1261-1263.
- 8. 肖胜. 激光惯导系统流水式旋转矢量算法研究[J]. 光学与光电技术, 2015, 13(4): 51-56.
- 9. 王真, 高凤岐, 高敏, 等. 旋转矢量多迭代捷联姿态解算误差补偿算法[J]. 中国测试, 2016, 42(8): 113-117.
- 10. 杨浩天, 汪立新, 王琪, 等. 一种改进的重叠式三子样圆锥误差补偿算法[J]. 电光与控制, 2017(3): 20-23.
