Advances in Applied Mathematics
Vol.
11
No.
11
(
2022
), Article ID:
58236
,
14
pages
10.12677/AAM.2022.1111858
具有媒体报道的埃博拉病毒SIQHR模型的 动力学分析
单美华,肖玉柱,宋学力,赵楠楠
长安大学理学院,陕西 西安
收稿日期:2022年10月21日;录用日期:2022年11月15日;发布日期:2022年11月23日

摘要
本文在SIQR模型的基础上建立了一类具有媒体报道、隔离以及患病者住院治疗的埃博拉病毒传染病SIQHR模型。首先,运用下一代生成矩阵方法计算出模型的基本再生数。其次,通过构造lyapunov函数证明了无病平衡点和地方病平衡点的稳定性。最后,通过数值模拟验证了媒体报道、隔离以及住院治疗对埃博拉病毒传染病的影响效果。数值模拟结果说明了媒体报道可以有效控制埃博拉病毒的传播。
关键词
埃博拉病毒,媒体报道,Lyapunov函数,全局稳定性

Dynamic Analysis of SIQHR Model with Media Coverage of Ebola Virus Infection
Meihua Shan, Yuzhu Xiao, Xueli Song, Nannan Zhao
School of Science, Chang’an University, Xi’an Shaanxi
Received: Oct. 21st, 2022; accepted: Nov. 15th, 2022; published: Nov. 23rd, 2022

ABSTRACT
On the basis of SIQR model, this paper establishes a class of SIQHR models for Ebola virus infectious diseases with media reports, isolation, and hospitalization of sick patients. Firstly according to the next generation theory, the basic reproduction number were calculated. Second, we demonstrate the stability of the disease-free equilibrium and the endemic equilibrium by constructing the lyapunov function. Finally, the effects of media reports, isolation and hospitalization on Ebola virus infectious diseases were verified. The numerical simulation results show that media reports can effectively control the spread of Ebola virus.
Keywords:Ebola Virus, Media Reports, Lyapunov Function, Global Stability

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
传染病可能是对社会的一个警告,因为它们会给数百万人造成死亡、残疾和社会经济破坏,埃博拉病毒、结核病(TB)、肺炎、霍乱、疟疾、艾滋病毒等,是我们注意到的主要传染病。每年有超过1100万人死于传染病,包括早产和幼儿死亡 [1]。由于全球化的旅行和社交媒体的重大进步,有关这些疫情的信息传播得相当迅速,而这反过来可能会对实际的流行病产生深远的影响。人们认识到可能会对疾病传播的动态产生非常复杂的影响。一般来说,每当传染病爆发时,如电视节目、报纸、广播或在线社交网络等媒体都会报道传染病的传播信息,有关感染人数和死亡人数的报告会每日更新,这对控制疫情的必要性有重要影响 [2] [3] [4]。因此,媒体在减少和控制传染病爆发方面具有重要作用,媒体报道有助于改变与公共卫生相关的行为,它使人们了解传染病的最新情况,并提出了必要的控制方法,有意识采取这些做法的人是为了降低他们变为感染者的机会 [5]。此外,这些做法还可以改变该流行病的规模,提高宣传活动的力度可以增加人们对疾病传播的了解,并采取措施降低感染几率 [6]。因此,通过媒体开展宣传活动,可以提高人们对疾病的认识。
2007年,Liu等人研究了一类受媒体报道影响的EIH (E表示潜伏人群、I表示感染人群、H表示住院治疗人群)模型,来说明因为报告的传染病和住院人数而产生的心理影响,从而出现的传染病多次爆发甚至持续周期性振荡的可能机制。这种影响导致了在个人和社区层面上的回避和接触模式的变化,并将非线性函数 纳入模型中,显示了传播动力学的定性差异 [7]。2008年,Cui等人建立了SEI模型,以调查媒体报道对特定区域传染病(如SARS)传播和控制的影响。用 作为媒体报道的接触速率,它衡量病毒从感染者向易感个体的传播,如果 ,则传染率为常数。当然,传染率不仅与病毒或疾病的传播能力有关,而且与人口中每个易感个体对疾病的警惕性密切相关 [8]。2016年,Yan等人提出了一种模型是将媒介影响函数纳入到感染强度中,用 作为有效接触率,并通过添加媒介动态,增强了传统的流行病SEIR模型。使用非线性最小二乘估计来观测数据中确定模型中的最佳拟合参数值,还进行了不确定性和敏感性分析,以确定疾病爆发早期阶段的关键参数,以确定媒体对疫情的最终结果的影响。研究结果证实了个人对媒体报道的反应的重要性,行为的改变对新出现的传染病控制有重要的影响 [9]。2017年,G. O. Agaba分析了一种SIRS传染病模型,并考虑了在人群中与传播意识相关的行为变化。该模型包括两种类型的意识:与不知情和知情人群之间的直接接触相关的私人意识,以及公共宣传活动。模型中不同稳态的稳定性分析提供了关于疾病在人群中的潜在传播的信息,以及疾病动态如何受到这两种意识的影响。数值模拟说明了系统在不同动力学状态下的行为,结果表明:感染的传播和受感染者的人数都减少了 [10]。
2018年,王等人研究了一类受媒体报道影响的SIRS传染病模型分析,其中 表示媒体报道对传染率的影响,通过数值模拟得到结论:媒体报道可以降低感染者的数量,也可以使得缩短疾病灭绝的时间 [11]。2020年,Chang等人,根据湖北省冠状病毒病2019 (COVID-19)疫情流行情况,提出了一种带有媒体报道的SIHRS疫情模型。使用数据进行数值模拟验证分析结果,观察高峰时间的影响和疾病传播的规模主要考虑不同的信息实现率和接触率。结果表明,随着信息实施率的降低,确诊病例的高峰将会延迟达到,并将显著增加。因此,为了在复工后采取更好的预防措施,非常有必要保持信息量和媒体报道的实施率 [12]。
因此,深入探索多种疫情相关信息的传播和大众媒体的报道如何影响疫情的传播具有重要意义 [13]。媒体影响对降低疾病流行率有重大影响,可以同时提高个人卫生和个人防护意识来降低受感染个体控制流行病的传播 [14]。以上文献通过采用了不同的影响因子来分析传染病的动力学性质,常见的减少因子有饱和函数的 [3] [8] [15] 或指数的 [7] [16] 增长函数。基于以上文献,本文采用媒体报道下的传染率 和媒体报道下的隔离率 ,研究了具有媒体报道、隔离和住院治疗的SIQHR传染病模型对埃博拉病毒的影响。
2. 模型的建立
本文将埃博拉病毒流行区域t时刻的总人口数 分为五个仓室:易感人群 ,感染人群 ,隔离人群 ,住院治疗人群 ,恢复人群 ,即 。用影响因子 表示媒体报道下的感染率,用 表示媒体报道下的隔离率,建立以下传染病模型:
(1)
其中A表示人群的输入率;d表示人类自然死亡率; 表示患病者的因病死亡率; 表示染病者的隔离比率; 表示媒体影响下隔离强度的最大增强作用; 表示感染者的传染率; 表示媒体报道对疾病的削减作用,媒体报道不能完全阻断传染病的传播,所以 ; 表示染病者的康复率; 表示隔离者的康复率; 表示住院治疗者的康复率; 表示患病者的治疗率; 表示隔离者的治疗率; 表示媒体报道下影响传染率的饱和函数, 表示媒体报道下影响隔离率的饱和函数, 和 满足条件:
1) ,。
2) ,。
3) ,。
4) 为模型(1)的发病率, 。
将模型(1)中的5个方程相加可以得到
则模型(1)的正向不变集为 。接下来在Y中研究模型(1)解的动力学性质。
3. 平衡点的存在性
研究模型(1)的动力学性质,首先需要确定平衡点,故先讨论无病平衡点以及地方病平衡点的存在性。模型(1)存在疾病消亡的无病平衡点 ,其中 。根据文献 [17] 中的下一代生成矩阵的方法可得模型的基本再生数为
定理1. 当 时,模型(1)仅存在无病平衡点 ;当 时,模型(1)不仅存在无病平衡点 ,而且还存在唯一的地方病平衡点 。
证明:根据计算得到模型(1)总有一个无病平衡点 。当 时,模型(1)还存在唯一的地方病平衡点 。令模型(1)的右端等于0,地方病平衡点 若存在,则应满足方程组
(2)
由方程组(2)的第二个方程可得
(3)
由方程组(2)的第三个方程可得
(4)
将方程(4)代入方程组(2)的第四个方程可得
(5)
方程组(2)的前两个方程相加得
(6)
定义方程(3)和方程(6)
(7)
(8)
令 ,显然 为严格单调递减函数,令 ,对 求导得
(9)
所以 为单调递增函数,从而 是严格单调递减函数。
当 时, ,且 ,,于是 ,则存在唯一的 使得 ,将 代入到方程组(2)中得
因此,当 时,模型(1)不仅存在无病平衡点 ,而且还存在唯一的地方病平衡点 。综上,模型(1)的无病平衡点和地方病平衡点的存在性得证。
4. 无病平衡点的稳定性和吸引性
定理2. 当 时,无病平衡点 是局部渐近稳定的;当 时,无病平衡点 是不稳定的。
证明:模型(1)在无病平衡点 处的雅可比矩阵为
(10)
矩阵(10)对应特征方程为
(11)
由方程(11)知,前三个特征根 ,, 均小于零。另外两个特征根满足方程: ,其中, ,。设其它两个特征根为 ,由韦达定理可知 满足:
(12)
综上得当 时,有 ,,即 ,,则方程(11)的所有特征根均为负,由Routh-Hurwitz判据可知,无病平衡点 是局部渐近稳定的,当 时, ,方程存在一个正根,无病平衡点 不稳定。
定理3. 当 时,无病平衡点 是全局渐近稳定的;当 时,无病平衡点 是全局吸引的。
证明:当 时,构造Lyapunov函数 ,求 关于t的导数得,
(13)
令 ,在O内当 时, ,,,,所以 是O的最大 不变集。由LaSalle不变集定理 [18] 可知,O内的任何轨线都趋于 ,因此 是全局渐近稳定的。
当 时,有
(14)
令 ,所以 是 的最大 不变集。由LaSalle不变集定理可知,无病平衡点 是全局吸引的。
根据以上两个定理知道,当 时,无病平衡点 是全局渐近稳定的;当 时,无病平衡点 是全局吸引的;当 时,无病平衡点 是不稳定的,疾病将趋于一个流行趋势。从而无病平衡点的稳定性和吸引性得证。
5. 地方病平衡点的全局稳定性
以下部分讨论地方病平衡点的全局稳定性,观察可知模型(1)的前四个方程与R无关,所以考虑以下子系统:
(14)
则可以看出集合 是系统(14)的正向不变集。 , 是系统(9)的无病平衡点和唯一的地方病平衡点。由定理1知,当 时,系统(14)有唯一的地方病平衡点,其中 ,,,。
定理4. 当 时,系统(14)的地方病平衡点 是局部渐近稳定的。
证明:系统(14)在 处的雅可比矩阵为
(15)
其中,
矩阵(15)对应的特征方程为
(16)
将(16)式展开得到
(17)
其中,
经计算得到 ,,,系统(15)的所有主子式均大于0,并且所有特征根都具有负实部,因此,由Routh-Hurwitz判据可知,当 时,系统(14)的地方病平衡点 是局部渐近稳定的。定理得证。
定理5. 当 时,系统(14)的地方病平衡点 全局渐近稳定。
证明:构造lyapunov函数
(18)
当 ,当且仅当 时 ,
则有 ,对L关于模型(14)求导数得
因此, ,当且仅当 时, ,于是由LaSalle不变集原理 [18] 可知,当 时,系统(14)的地方病平衡点 是全局渐近稳定的。定理得证。
6. 数值模拟
本小节对模型进行数值模拟,选取 ( 表示媒体报道下易感者对埃博拉病毒信息认识的偏差程度, 表示媒体报道下采取隔离措施的相关部门对埃博拉病毒信息认识的偏差程度),取初始值为 ,取参数值 ,,,,,,,,,,,,,,计算得到 ,无病平衡点 是全局渐近稳定的,如图1所示。初始值保持不变,取参数为 ,,,,,,,,,,,,计算得到 ,地方病平衡点 是全局渐近稳定的,如图2所示。
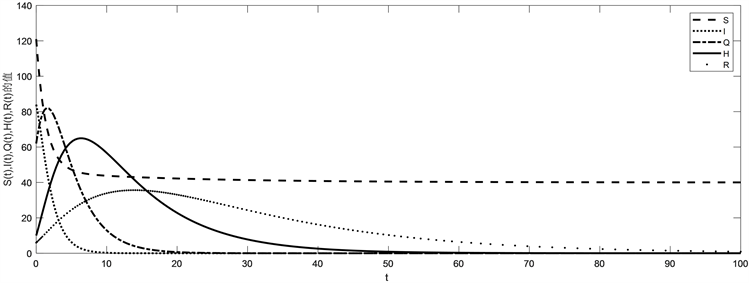
Figure 1. Stability of the disease-free equilibrium
图1. 无病平衡点的稳定性
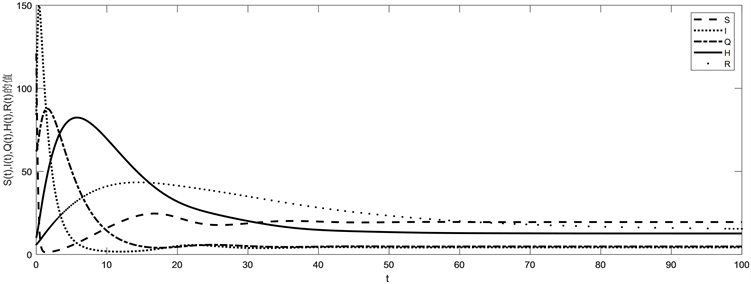
Figure 2. Stability of the endemic equilibrium
图2. 地方病平衡点的稳定性

Figure 3. Effect of isolation rate and inpatient treatment rate on the basic reproduction number
图3. 隔离率 和患病者住院治疗率 对基本再生数 的影响
图3是隔离率 和患病者的住院治疗率 对基本再生数 的综合影响,结果表明随着隔离率 和患病者的住院治疗率 的增加,基本再生数 的值在不断减小,基本再生数 减小,表明隔离率 和患病者的住院治疗率 对于埃博拉病毒的传播具有控制作用。图4分别表明,当 时,图4(a)表明媒体报道缩短了埃博拉病毒易感人群趋于稳定的时间,图4(b)~(d)分别表明媒体报道对于埃博拉病毒感染者、隔离者和住院治疗者趋于消亡的时间明显缩短了,即媒体报道加快了埃博拉病毒传染病的消亡。图5分别表明,当 时,图5(a)表明媒体报道使得易感者的人数增加,图5(b)~(d)分别表明媒体报道对于埃博拉病毒感染者、隔离者和住院治疗者有所减少并且疾病趋于稳定的时间缩短了,即媒体报道增加易感者的同时,降低了感染者、隔离者和住院治疗者的人数,减少了疾病趋于稳定的时间。
7. 结论
本文采用媒体报道下的传染率 和媒体报道下的隔离率 建立了一类具有媒体报道、隔离以及住院治疗的埃博拉病毒SIQHR传染病模型。根据基本再生数 推导了无病

Figure 4. Impact of media reports on the disease-free equilibrium of
图4. 媒体报道对无病平衡点 的影响
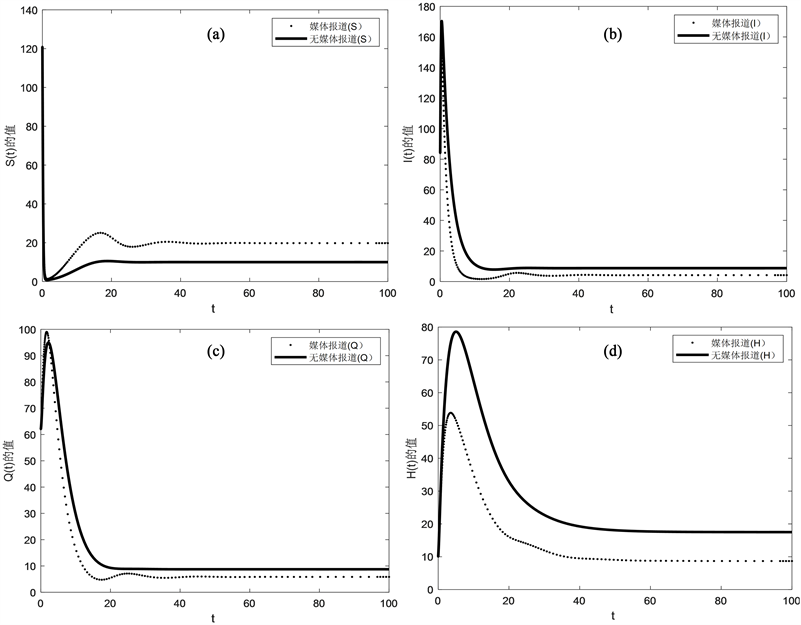
Figure 5. Impact of media reports on the endemic equilibrium of
图5. 媒体报道对地方病平衡点 的影响
平衡点和地方病平衡点的存在性和稳定性。通过MATLAB对模型进行数值模拟,数值模拟验证了无病平衡点和地方病平衡点的稳定性,并且考虑了 (隔离率)和 (感染者的住院治疗率)对 的综合影响,随着隔离率和感染者的住院治疗率的增加,基本再生数 的值在不断减小;观察媒体报道、对感染者隔离以及住院治疗对埃博拉病毒传染病的影响效果。得出结论:对感染者进行隔离和住院治疗可以有效控制埃博拉病毒的传播,并且媒体报道缩短了埃博拉病毒趋于消亡的时间;随着人们对媒体报道信息度认识度的准确性的提高,人们减少去有易感者和人员密集的场所,从而与他人接触的机会减少了,那么感染者的数量、隔离者人数以及住院治疗者的人数也减少了,使得埃博拉病毒趋于稳定的时间缩短了。埃博拉病毒得到了有效的控制。
致谢
首先要感谢我的导师肖老师,他在繁忙的教学工作中挤出时间很细心地修改我的论文。研一刚开始老师就开始细心培养我们,让我们每周看一篇文献并且去给老师汇报自己看完文献的想法以及论文的创新点与不足之处或者有什么可以改进的地方。在看了一部分文献之后,需要确定自己的研究方向,在我们很迷茫不确定自己方向的时候,老师会给我们指引方向,让我们有个小方向,再看看我们对这些方向感不感兴趣,从而确定自己的方向。其次要感谢宋老师和赵老师,在我们撰写论文过程中遇到过很多问题:在我们理论推导有问题,程序编写有问题时,老师们都会细心给我们指出问题并解决问题。总而言之,从初稿到定稿,几位老师对我们都十分的严格,包括字体、格式和标点符号每一个细节。老师每次对我的疑问给予细心的解答并给出一些建议,对我的论文进行细心的修改,使得我的论文结构一步一步的完善,内容也逐渐的变得充实,这期间我的同门对我也有很大帮助,体现出了同学情。
最后,还要感谢教过我的任课老师,你们在教学过程中对待上课的热情以及对待工作认真负责一直是我学习和工作中的榜样,再次感谢老师们和同门对我的帮助和指导。
基金项目
基金项目:中央高校基本科研业务费资助项目(自然科学类) (批准号:300102122113)。
文章引用
单美华,肖玉柱,宋学力,赵楠楠. 具有媒体报道的埃博拉病毒SIQHR模型的动力学分析
Dynamic Analysis of SIQHR Model with Media Coverage of Ebola Virus Infection[J]. 应用数学进展, 2022, 11(11): 8094-8107. https://doi.org/10.12677/AAM.2022.1111858
参考文献
- 1. Lau, J.T.F., Yang, X., Tsui, H.Y., et al. (2005) Impacts of SARS on Health-Seeking Behaviors in General Population in Hong Kong. Preventive Medicine, 41, 454-462. https://doi.org/10.1016/j.ypmed.2004.11.023
- 2. Liu, M., Chang, Y. and Zuo, L. (2016) Modelling the Impact of Media in Controlling the Diseases with a Piecewise Transmission Rate. Discrete Dynamics in Nature and Society, 2016, Article ID: 3458965. https://doi.org/10.1155/2016/3458965
- 3. Tchuenche, J.M., Dube, N., Bhunu, C.P., et al. (2011) The Impact of Media Coverage on the Transmission Dynamics of Human Influenza. BMC Public Health, 11, S5. https://doi.org/10.1186/1471-2458-11-S1-S5
- 4. Majumder, M.S., Kluberg, S., Santillana, M., et al. (2015) 2014 Ebola Outbreak: Media Events Track Changes in Observed Reproductive Number. PLoS Currents, 7.
- 5. Jones, J.H. and Salathé, M. (2009) Early Assessment of Anxiety and Behavioral Response to Novel Swine-Origin Influenza A (H1N1). PLOS ONE, 4, e8032. https://doi.org/10.1371/journal.pone.0008032
- 6. Rubin, G.J., Amlôt, R., Page, L., et al. (2009) Public Perceptions, Anxiety, and Behaviour Change in Relation to the Swine Flu Outbreak: Cross Sectional Telephone Survey. BMJ, 339, b2651. https://doi.org/10.1136/bmj.b2651
- 7. Liu, R., Wu, J. and Zhu, H. (2007) Media/Psychological Impact on Multiple Outbreaks of Emerging Infectious Diseases. Computational and Mathematical Methods in Medicine, 8, 153-164. https://doi.org/10.1080/17486700701425870
- 8. Cui, J., Sun, Y. and Zhu, H. (2008) The Impact of Media on the Control of Infectious Diseases. Journal of Dynamics and Differential Equations, 20, 31-53. https://doi.org/10.1007/s10884-007-9075-0
- 9. Yan, Q., Tang, S., Gabriele, S., et al. (2016) Media Coverage and Hospital Notifications: Correlation Analysis and Optimal Media Impact Duration to Manage a Pandemic. Journal of Theoretical Biology, 390, 1-13. https://doi.org/10.1016/j.jtbi.2015.11.002
- 10. Agaba, G.O., Kyrychko, Y.N. and Blyuss, K.B. (2017) Mathemati-cal Model for the Impact of Awareness on the Dynamics of Infectious Diseases. Mathematical Biosciences, 286, 22-30. https://doi.org/10.1016/j.mbs.2017.01.009
- 11. 王俊荣, 窦霁虹, 孙梦皎. 受媒体报道影响的具有Logistic人口变化的SIRS传染病模型分析[J]. 陕西师范大学学报: 自然科学版, 2018, 46(6): 46-53.
- 12. Chang, X., Liu, M., Jin, Z., et al. (2020) Studying on the Impact of Media Coverage on the Spread of COVID-19 in Hubei Province, China. Mathematical Biosciences and Engineering, 17, 3147-3159. https://doi.org/10.3934/mbe.2020178
- 13. Wang, Z. and Xia, C. (2020) Co-Evolution Spreading of Multiple In-formation and Epidemics on Two-Layered Networks under the Influence of Mass media. Nonlinear Dynamics, 102, 3039-3052. https://doi.org/10.1007/s11071-020-06021-7
- 14. Tiwari, P.K., Rai, R.K., Gupta, R.K., et al. (2022) Modeling the Control of Bacterial Disease by Social Media Advertisements: Effects of Awareness and Sanitation. Journal of Biological Systems, 30, 51-92.
- 15. Sun, C., Yang, W., Arino, J., et al. (2011) Effect of Media-Induced Social Distancing on Dis-ease Transmission in a Two Patch Setting. Mathematical Biosciences, 230, 87-95. https://doi.org/10.1016/j.mbs.2011.01.005
- 16. Tchuenche, J.M. and Bauch, C.T. (2012) Dynamics of an Infec-tious Disease Where Media Coverage Influences Transmission. International Scholarly Research Notices, 2012, Article ID: 581274. https://doi.org/10.5402/2012/581274
- 17. Van Driessche, P. and Watmough, J. (2002) Reproduction Numbers and Sub-Threshold Endemic Equilibria for Compartmental Models of Disease Transmission. Mathematical Biosciences, 180, 29-48. https://doi.org/10.1016/S0025-5564(02)00108-6
- 18. La Salle, J.P. (1976) The Stability of Dynamical Systems. Society for Industrial and Applied Mathematics, University City.