Advances in Applied Mathematics
Vol.
11
No.
01
(
2022
), Article ID:
48470
,
10
pages
10.12677/AAM.2022.111066
Conformable分数阶单机无穷大电力系统的 混沌容错同步
张群力,付雪荣,魏莹
菏泽学院数学与统计学院,山东 菏泽
收稿日期:2021年12月26日;录用日期:2022年1月16日;发布日期:2022年1月29日

摘要
基于反演设计和容错控制研究Conformable分数阶单机无穷大电力系统的混沌同步问题,在设计过程中引入虚拟的误差函数,利用李雅普诺夫稳定性理论确保带有执行器故障的被控系统的鲁棒同步,最后,模拟结果表明所提控制策略的有效性。
关键词
单机无穷大电力系统,容错同步,Conformable分数阶导数,反演设计

Tolerant Synchronization Analysis for Conformable Fractional Order Unipolar Infinite Power System
Qunli Zhang, Xuerong Fu, Ying Wei
College of Mathematics and Statistics, Heze University, Heze Shandong
Received: Dec. 26th, 2021; accepted: Jan. 16th, 2022; published: Jan. 29th, 2022

ABSTRACT
A synchronization strategy based on backstepping design and tolerant control is studied for conformable fractional order unipolar infinite power system. The virtual control error functions are introduced in the design, and the Lyapunov stability theory is used to ensure the robust synchronization of the controlled systems with the actuator faults. Finally, the simulation results show the effectiveness of the proposed control strategy.
Keywords:Unipolar Infinite Power System, Tolerant Synchronization, Conformable Fractional Order Derivative, Backstepping Design

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
分数阶微积分是当前非线性研究领域的热点,能够较准确简洁地阐述具有历史记忆性和空间全域相关性等力学与物理过程,在量子力学、电磁振动、材料力学等领域有着十分广泛的应用 [1] [2] [3]。Khalil等 [4] 提出一种表现形式简洁易懂的Conformable分数阶微分定义,与整数阶微分有着良好分析、计算等统一 [5],受到学者们的极大关注。Atangana等 [6] 继续发展了Conformable分数阶微分理论,为后继学者的研究奠定了基础。Feng和Meng [7] 根据Conformable分数阶微积分性质,研究了一类Conformable分数阶动力学方程的振荡和渐近性质。当前国内外关于Conformable分数阶微分的研究虽然有一些代表性成果 [7] [8] [9] [10] [11],但尚处于初期阶段。
近年来,研究成果为数不多的容错控制已经成为一种有效的增加系统安全和可靠性的方法 [12] [13] [14] [15],其设计方法一般有:被动方法、主动方法,即使故障发生,被控系统仍能保持渐近稳定。反演法 [16] [17] [18] [19] [20] 可将复杂的系统分解成不超过原系统阶数的子系统,通过设计中间虚拟控制量、修正虚拟控制律确保系统的稳定性,是一种性能优良的控制方法。Zhang等 [16] 设计反演控制器,对Morse吸引子做了混沌同步分析。Deng等 [17] 通过引入辅助信号,引入基于期望轨迹的前馈补偿概念,提出了一种实用的输出反馈反演控制器,用于液压执行器的运动控制。Zhang等 [19] 针对磁浮列车系统的稳定悬浮控制问题,设计了基于反步法的非线性控制器。Su等 [20] 在控制设计中引入虚拟控制函数,使用改进的自适应定律估计外部扰动的未知边界,利用未知边界的更新值,为不确定的非线性系统合成一类连续自适应鲁棒状态反馈控制器。
有效对电力系统进行稳定分析、评估是保障电力系统安全稳定运行的前提,Zhang等 [21] 基于轨迹断面特征根研究了电力系统暂态稳定定量评估方法,Zhao等 [22] 考虑二次系统具有时滞,用新的Lyapunov-Krasovskii泛函构造函数和解析方法得到了稳定判据,Wang等 [23] 首先利用分岔图及相图对系统的基本动力学行为进行分析,然后借助递归型滑模控制方法为混沌电力系统设计励磁控制器并给出具体表达式。如今单机无穷大系统模式在现实中的应用较为关注,文献 [24] [25] [26] [27] [28] 采用多种控制方法对系统性能指标进行稳定性分析。Yan [29] 采用Lyapunov指数谱、分岔图和吸引子相图分析了Conformable分数阶单机无穷大电力系统的分岔和混沌现象。整数阶电力系统模型已经无法满足研究需要,分析Conformable分数阶单机无穷大电力系统混沌振荡产生的机理有着重要的理论和实际意义 [29] [30] [31] [32]。
本文基于容错控制理论,设计中间虚拟控制量,通过修正虚拟控制律,基于反演方法设计带有执行器故障的控制器,研讨Conformable分数阶单机无穷大电力系统混沌同步问题。
2. 基本理论
定义:函数 的conformable分数阶导数为
注:函数 可导,则有 。
定理1:若 ,则有 。
证明:
所以有 成立。
定理2:设 ,则 ,有
其中函数 满足 。
证明: ,。
于是有
由定理1,得
由于 关于 单调递减,所以
3. 实例及数值仿真
带有执行器故障函数得Conformable分数阶单机无穷大电力系统混沌微分方程 [29] [30] 为驱动系统:
(1)
其中 , 是执行器故障函数。
响应系统为:
(2)
其中 是 的估计。
设误差 ,,则有如下结论:
定理3:若执行器故障误差 是关于t的可导函数,满足
(3)
当存在常数 ,满足
, (4)
时,驱动系统(1)和响应系统(2)混沌同步。
证明:由(1)和(2)得误差系统:
(5)
由定理2和误差系统(5)中的第一个方程得:
令 ,则 ,
设 ,则结合(5)中第一、二个方程有
再次用定理2得:
令 ,则有
于是有 ,。
设 ,则结合(5)中第一、二、三个方程有
再次利用定理2得:
令 ,则有
由条件(4)中 知, ,。
设 ,则结合(5)中第一、二、三、四个方程有
再次利用定理2和(3)得:
其中 。由条件(4)知,
我们取 ,满足条件(4),得到conformable分数阶单机无穷大电力系统(1)和(2)的混沌同步情况(见图1~4)。

Figure 1. Synchronization for state vectors
图1. 状态分量 同步
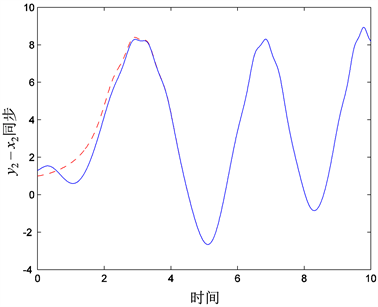
Figure 2. Synchronization for state vectors
图2. 状态分量 同步
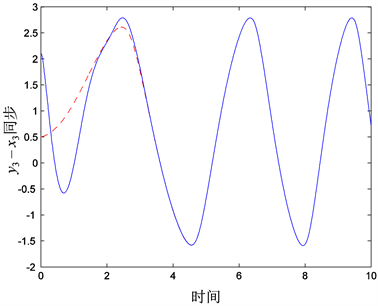
Figure 3. Synchronization for state vectors
图3. 状态分量 同步
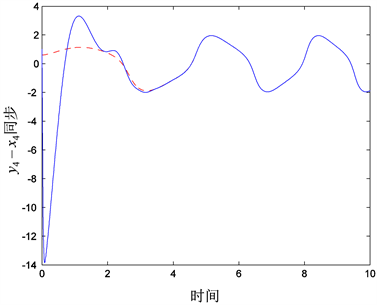
Figure 4. Synchronization for state vectors
图4. 状态分量 同步
注:当系统(1)、(2)中的第一二三个方程也存在执行器故障函数时,可模仿定理的推导得到类似结论。
4. 结论
本文基于容错控制、反演设计研究了Conformable分数阶单机无穷大电力系统的混沌同步问题。在故障存在的情况下,合理假设中间误差函数用反演法设计出控制器,仍能使系统具有渐近稳定性。
致谢
本文十分感谢山东省自然科学基金(项目编号:ZR2020QA002,ZR2017MA029)的资助。
文章引用
张群力,付雪荣,魏 莹. Conformable分数阶单机无穷大电力系统的混沌容错同步
Tolerant Synchronization Analysis for Conformable Fractional Order Unipolar Infinite Power System[J]. 应用数学进展, 2022, 11(01): 590-599. https://doi.org/10.12677/AAM.2022.111066
参考文献
- 1. Torvik, P.J. and Bagley, R.L. (1984) On the Fractional Derivative in the Behavior of Real Materials. Journal of Applied Mechanics, 51, 725-728. https://doi.org/10.1115/1.3167615
- 2. Tarasov, V.E. and Zaslavsky, G.M. (2006) Fractional Dynamics of Coupled Oscillators with Long-Rang Interaction. Chaos, 16, Article ID: 023110.
- 3. Bolotin, K.L., Ghahari, F., Shulman, M.D., et al. (2009) Observation of the Fractional Quantum Hall Effect in Grapheme. Nature, 462, 196-199. https://doi.org/10.1038/nature08582
- 4. Khalil, R., Horani, M.A., Yousef, A., et al. (2014) A New Definition of Fractional Derivative. Journal of Computational & Applied Mathematics, 264, 65-70. https://doi.org/10.1016/j.cam.2014.01.002
- 5. Zhao, D.Z., Pan, X.Q. and Luo, M.K. (2018) A New Framework for Multivariate General Conformable Fractional Calculus and Potential Applications. Physica A, 510, 271-280. https://doi.org/10.1016/j.physa.2018.06.070
- 6. Atangana, A., Baleanu, D. and Alsaedi, A. (2015) New Properties of Conformable Derivative. Open Mathematics, 13, 889-898. https://doi.org/10.1515/math-2015-0081
- 7. Feng, Q. and Meng, F. (2018) Oscillation Results for a Fractional Order Dynamic Equation on Time Scales with Conformable Fractional Derivative. Advances in Difference Equations, 2018, Article No. 193. https://doi.org/10.1186/s13662-018-1643-6
- 8. Fernando, S., Davidson, M. and Marcelo, M. (2018) Conformable Laplace Transform of Fractional Differential Equations. Axioms, 7, Article 55. https://doi.org/10.3390/axioms7030055
- 9. Ruan, J., Sun, K., Mou, J., et al. (2018) Fractional-Order Simplest Memristor-Based Chaotic Circuit with New Derivative. The European Physical Journal Plus, 133, Article No. 3. https://doi.org/10.1140/epjp/i2018-11828-0
- 10. He, S.B., Sun, K.H. and Wang, H.H. (2019) Dynamics and Synchronization of Conformable Fractional-Order Hyperchaotic Systems Using the Homotopy Analysis Method. Communications in Nonlinear Science and Numerical Simulation, 73, 146-164. https://doi.org/10.1016/j.cnsns.2019.02.007
- 11. Unal, E. and Gokdogan, A. (2017) Solution of Conformable Fractional Ordinary Differential Equations via Differential Transform Method. Optik, 128, 264-273. https://doi.org/10.1016/j.ijleo.2016.10.031
- 12. Ye, D. and Zhao, X. (2014) Robust Adaptive Synchronization for a Class of Chaotic Systems with Actuator Failures and Nonlinear Uncertainty. Nonlinear Dynamics, 76, 973-983. https://doi.org/10.1007/s11071-013-1181-4
- 13. Zhang, Q. (2015) Chaotic Tolerant Synchronization Analysis with Propagation Delay and Actuator Faults. Mathematical Problems in Engineering, 2015, Article ID: 785861. https://doi.org/10.1155/2015/785861
- 14. 邓立为, 宋歌, 高俊山. 不确定混沌系统的鲁棒自适应容错同步控制[J]. 电机与控制学报, 2017, 21(8): 114-122.
- 15. 高俊山, 张玉双, 邓立为. 时滞混沌系统的鲁棒自适应容错同步控制[J]. 计算机仿真, 2020, 37(6): 247-261.
- 16. Zhang, Q. and Jia, G. (2006) Chaos Synchronization of Morse Oscillator via Backstepping Design. Annals of Differential Equation, 22, 456-460.
- 17. Deng, W.X., Yao, J.Y., et al. (2021) Out Feedback Backstepping Control of Hydraulic Actuators with Valve Dynamics Compensation. Mechanical Systems and Signal Processing, 158, Article ID: 107769. https://doi.org/10.1016/j.ymssp.2021.107769
- 18. Ma, J., Tao, H. and Huang, J.W. (2021) Observer Integrate Backstepping Control for a Ball and Plate System. International Journal of Dynamics and Control, 9, 141-148. https://doi.org/10.1007/s40435-020-00629-8
- 19. 张文跃, 佟来生, 朱跃欧, 等. 磁浮列车悬浮系统的反步控制方法及实验研究[J]. 科学技术与研究, 2021, 21(4): 1563-1567.
- 20. 粟世玮, 张思洋, 尤熠然, 等. 一类不确定非线性系统的鲁棒自适应Backstepping控制[J]. 电光与控制, 2020, 27(11): 10-16.
- 21. 张师, 于明鑫, 刘馨语. 基于轨迹断面特征根的电力系统暂态稳定定量评估[J]. 吉林电力, 2021, 49(5): 11-15.
- 22. 赵亚文, 丛屾. 广域电力系统动态稳定性分析的时滞系统方法[J]. 黑龙江大学工程学报, 2021, 12(1): 68-74.
- 23. 王江彬, 刘崇新. 带励磁限制环节混沌电力系统的励磁控制器设计[J]. 电工技术, 2021(10): 109-112.
- 24. 徐开军, 张李坚. 单机无穷大系统暂态稳定性仿真及分析[J]. 信息化研究, 2018, 44(6): 31-35.
- 25. 武以敏, 魏章志. 具有时滞的单机无穷大系统的随机稳定性[J]. 控制工程, 2018, 25(5): 799-803.
- 26. 高红亮, 詹习生, 朱军, 万里光. 基于H∞控制的单机无穷大电力系统输出反馈控制器设计[J]. 广西大学学报(自然科学版), 2019, 44(2): 396-403.
- 27. 康勇, 林新春, 郑云, 等. 新能源并网变换器单机无穷大系统的静态稳定极限及静态稳定工作区[J]. 中国电机工程学报, 2020, 40(14): 4506-4515.
- 28. 张雪娟, 孙士云, 郑新宇, 等. 含风电扩展单机无穷大系统不对称故障下的暂态稳定性分析[J]. 现代电力, 2020, 37(4): 368-375.
- 29. 严波, 贺少波. Conformable分数阶单机无穷大电力系统分岔与混沌研究[J]. 系统科学与数学, 2020, 40(6): 954-968.
- 30. Arredondo, J.M.R. (1999) Obtaining Dynamic Equations through the Minimization of a Line Flows Function. International Journal of Electrical Power& Energy Systems, 21, 365-373. https://doi.org/10.1016/S0142-0615(99)00005-8
- 31. 闵富红, 马美玲, 翟炜, 等. 基于继电特性函数的互联电力系统混沌控制[J]. 物理学报, 2014, 63(5): 1-8.
- 32. 倪骏康, 刘崇新, 庞霞. 电力系统混沌振荡的等效快速终端模糊滑模控制[J]. 物理学报, 2013, 62(19): 99-105.