Pure Mathematics
Vol.4 No.05(2014), Article
ID:14113,6
pages
DOI:10.12677/PM.2014.45029
Existence of Three Positive Solutions for a Class of Nonlinear Elliptic Systems
Department of Mathematics, College of Science, University of Shanghai for Science and Technology, Shanghai
Email: gmweixy@163.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jul. 6th, 2014; revised: Aug. 4th, 2014; accepted: Aug. 13th, 2014
ABSTRACT
Motivated by existence of solutions of single equation, in this paper we study the existence of multiple solutions of a class of nonlienar elliptic systems with nonhomogeneous boundary conditions. Using Guo-Krasnoselski’s fixed point theorem on cones, we prove that there exist at least three positive solutions for this class of nonlinear elliptic systems.
Keywords:Nonlinear Elliptic System, Positive Radial Solution, Fixed Point Theorem on Cones

一类非线性椭圆方程组三个正解的存在性
魏公明,陈雨彤,张兴丽
上海理工大学理学院数学系,上海
Email: gmweixy@163.com
收稿日期:2014年7月6日;修回日期:2014年8月4日;录用日期:2014年8月13日

摘 要
受对单个方程多解的存在性的研究的启发,本文研究具有非齐次边界条件的非线性椭圆方程组的存在性及多解性。由锥上Guo-Krasnoselskii不动点定理,本文证明了一类椭圆型方程组至少存在三个正解。
关键词
非线性椭圆方程组,正径向解,锥上不动点定理

1. 引言
本章主要考虑了下列问题三个正径向解的存在性
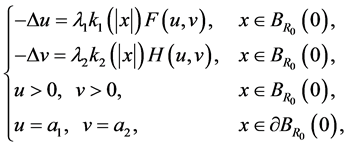 (1.1)
(1.1)
其中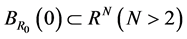 是一个以原点为球心
是一个以原点为球心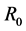 为半径的球,
为半径的球,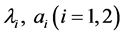 是正参数,
是正参数, 是在
是在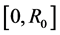 的任何子区间上都不恒等于零的连续函数.
的任何子区间上都不恒等于零的连续函数.
本文假设成立下列条件:
(H1)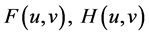 是关于
是关于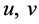 的连续递增函数,即:当
的连续递增函数,即:当 时,有
时,有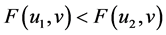 ,
,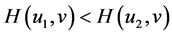 成立;当
成立;当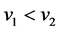 时,有
时,有 ,
,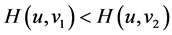 成立。
成立。
(H2) 对任意的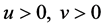 ,有
,有 成立。
成立。
(H3) 对任意的 ,有
,有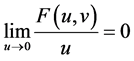 成立;对任意的
成立;对任意的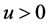 ,有成
,有成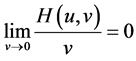 立。
立。
(H4) 对任意的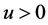 ,有
,有 成立;对任意的
成立;对任意的 ,有
,有 成立。
成立。
(H5) 存在非负函数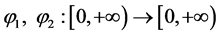 满足
满足
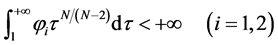
且存在正常数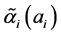 ,
,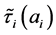 ,
,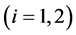
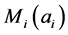 ,使得对任意的
,使得对任意的 ,都有下式成立
,都有下式成立
当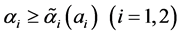 时,有
时,有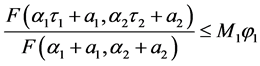 ,
,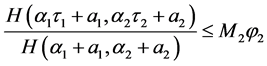 成立
成立
本文的主要结果如下
定理1.1:若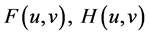 满足(H1)~(H5),则对任意的
满足(H1)~(H5),则对任意的 ,问题(1.1)至少有一个解。
,问题(1.1)至少有一个解。
定理1.2:若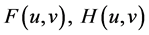 满足(H1)~(H5),并且存在
满足(H1)~(H5),并且存在 使得对任意的
使得对任意的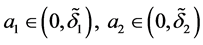 ,存在
,存在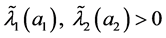 ,当
,当 时,方程组(1.1)至少存在三个正的径向解。
时,方程组(1.1)至少存在三个正的径向解。
本文的证明主要基于著名的Krasnoselskii的不动点定理。这种方法已经得到广泛的应用,如文献[1] 用这种方法研究了单个方程解的存在性和单个方程的多解性,文献[2] -[4] 用不同的方法考虑了非线性Schrodinger方程组类似的问题,文献[5] [6] 主要运用锥上不动点定理和Green函数研究了非线性方程组的多解性。在这些文献的启发下,可以把本文的问题转化为常微分方程的问题,通过不动点理论得到多个不动点的存在性。
2. 预备知识
本文的主要目的是研究问题(1.1)多个正径向解的存在性。现把偏微分方程转化为常微分方程。令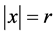 ,并且用
,并且用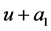 ,
,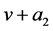 来代替
来代替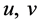 ,所以方程组(1.1)可化为齐次边界条件的常微分方程
,所以方程组(1.1)可化为齐次边界条件的常微分方程
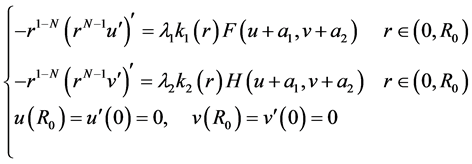 (2.1)
(2.1)
令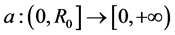 ,
,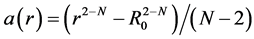 ,使
,使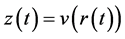 ,
, ,
,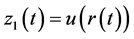 ,则(2.1)可化为
,则(2.1)可化为
 (2.2)
(2.2)
其中 ,
, ,是在
,是在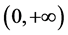 的任何子区间都不退化为零的连续函数。应用边值条件,对(2.2)两次积分,则得到与(2.2)等价的下列积分方程
的任何子区间都不退化为零的连续函数。应用边值条件,对(2.2)两次积分,则得到与(2.2)等价的下列积分方程
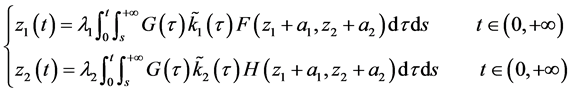 (2.3)
(2.3)
其中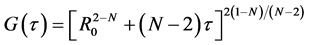 ,因此(2.3)的不动点就是(2.1)的解。本章将用到下列著名的不动点定理,如文献[7] [8] 。此不动点定理已经被运用到非线性方程组,如文献[9] 。
,因此(2.3)的不动点就是(2.1)的解。本章将用到下列著名的不动点定理,如文献[7] [8] 。此不动点定理已经被运用到非线性方程组,如文献[9] 。
定理2.1: 是一个Banach空间,
是一个Banach空间, 是
是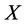 上的一个锥。假设
上的一个锥。假设 是
是 的非空开集,并且
的非空开集,并且 ,
,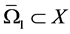 ,令
,令 是一个全连续算子,如果下列条件其中之一成立
是一个全连续算子,如果下列条件其中之一成立
(1) 如果 ,则
,则 ,且如果
,且如果 ,则
,则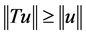 ;
;
(2) 如果 ,则
,则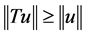 ,且如果
,且如果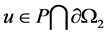 ,则
,则 。
。
则![]() 在
在 上有一个不动点。
上有一个不动点。
为了应用定理2.1,可设Banach空间为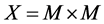 ,定义范数为
,定义范数为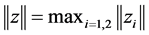 ,其中
,其中 ,
, 代表的是有界连续函数
代表的是有界连续函数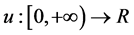 空间,定义范数为
空间,定义范数为 。
。
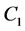 是
是 的一个锥,元素是非负连续凸函数,满足
的一个锥,元素是非负连续凸函数,满足 ,且是单调递增函数。令
,且是单调递增函数。令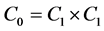 ,则
,则 是
是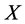 的一个锥。
的一个锥。
映射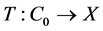 ,其中
,其中 ,定义如下
,定义如下

通过分步积分,对任意的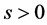 ,有下式成立
,有下式成立

所以![]() 的定义是合理的,
的定义是合理的,![]() 的不动点就是方程组(2.2)的解.
的不动点就是方程组(2.2)的解.
3. 主要结果的证明
引理3.1: ,且
,且![]() 是一个全连续算子,即
是一个全连续算子,即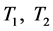 是全连续算子。
是全连续算子。
证明:因为

所以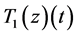 是单调递增的凸函数。同样的方法证明
是单调递增的凸函数。同样的方法证明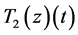 也是单调递增的凸函数。即
也是单调递增的凸函数。即 。
。
现在证明![]() 是全连续算子。首先证明
是全连续算子。首先证明![]() 是紧算子,令
是紧算子,令 且满足
且满足 ,
,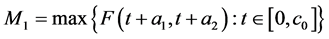 ,
,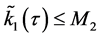 。则下式成立
。则下式成立

通过Arzela-Ascoli紧性条件,可以假设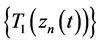 在
在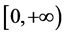 的任意紧子空间都一致收敛。为了证明
的任意紧子空间都一致收敛。为了证明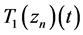 有一致收敛子列,只需给定一个
有一致收敛子列,只需给定一个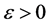 ,存在
,存在 满足
满足
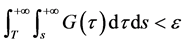
由文献[10] 的命题1可得,![]() 是一个紧算子。
是一个紧算子。
下面证明![]() 是一个连续算子。令
是一个连续算子。令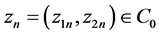 且满足当
且满足当![]() 时,
时,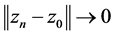 ,其中
,其中 ,即是
,即是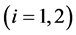
 。所以
。所以

其中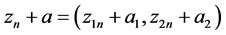 ,
,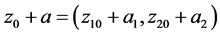 ,因为
,因为 ,
, 是连续函数,则对
是连续函数,则对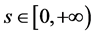 ,任给一个
,任给一个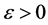 ,存在一个自然数
,存在一个自然数 ,当
,当 时,有
时,有
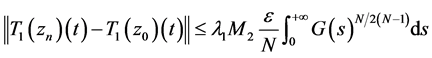
所以当![]() 时,
时, ,即可得
,即可得![]() 是连续算子,所以
是连续算子,所以![]() 是全连续算子。同理可证明
是全连续算子。同理可证明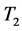 是全连续算子。因此
是全连续算子。因此![]() 是全连续算子.
是全连续算子.
给定 ,且
,且 ,则存在唯一的
,则存在唯一的 且
且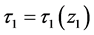 ,
, 满足
满足

定义:

引理3.2: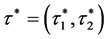 是正的,即
是正的,即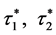 是正实数,且
是正实数,且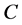 是
是![]() 下的一个不变锥。
下的一个不变锥。
证明:首先证明 是一个正实数。假设
是一个正实数。假设 ,则存在一个序列
,则存在一个序列 满足
满足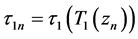 是一个严格递增并且收敛于
是一个严格递增并且收敛于![]() 的正实数序列。通过
的正实数序列。通过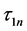 的定义,有下式成立
的定义,有下式成立
 即
即
 , (3.1)
, (3.1)
其中 ,有(3.1)并通过积分可得
,有(3.1)并通过积分可得
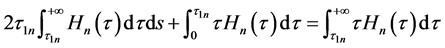 . (3.2)
. (3.2)
由(3.2)可知
 (3.3)
(3.3)
令 ,其中
,其中 ,
,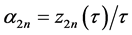 。由(H1)可知,当
。由(H1)可知,当 时,
时,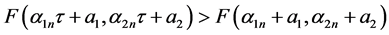 。又由(3.3)可得
。又由(3.3)可得

即

亦即
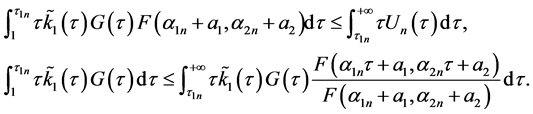 (3.4)
(3.4)
考虑下列两种情况
(1) 存在一个子序列 ,其中
,其中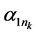 是
是 的子序列,
的子序列,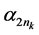 是
是 的子序列,并满足,对任意的
的子序列,并满足,对任意的 ,有
,有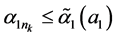 ,
, 。由(3.4)和(H5)可得
。由(3.4)和(H5)可得

(2) 对任意的 ,
,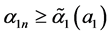 ,
, 时,有(3.4)和假设(H5)可得
时,有(3.4)和假设(H5)可得

因为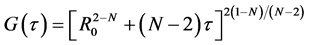 ,两种情况均可得到
,两种情况均可得到

由(H5)知,当![]() 时,上面不等式右边的积分收敛于0,但这是不可能的,因为
时,上面不等式右边的积分收敛于0,但这是不可能的,因为 。
。
因此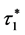 是正实数,同理可证明
是正实数,同理可证明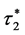 是正实数。容易证明
是正实数。容易证明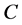 是
是![]() 不变锥,这里不再给出证明。
不变锥,这里不再给出证明。
引理3.3:假设(H2)成立,给定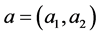 ,
, ,且
,且 都是正数,则存在足够大的
都是正数,则存在足够大的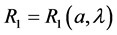 满足下式
满足下式
 (3.5)
(3.5)
证明:由(H4)可得,给定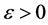 ,存在
,存在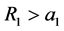 ,且当
,且当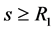 时,对任意的
时,对任意的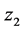 ,有下列不等式成立
,有下列不等式成立
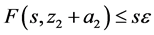
因此对任意的 ,下式成立
,下式成立
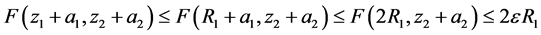
即得
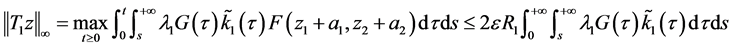
令 ,即证明了对任意的
,即证明了对任意的 ,有下式成立
,有下式成立
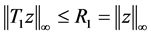
同理可证明对任意的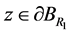 ,下式成立
,下式成立
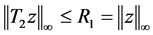
这样就证明了(3.5)。
引理3.4:假设(H2)成立,给定 ,
,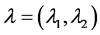 ,且
,且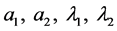 都是正实数,则存在足够小的
都是正实数,则存在足够小的 满足下式
满足下式

证明:因为 ,给定
,给定 ,存在足够小的
,存在足够小的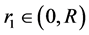 ,使得下式成立
,使得下式成立
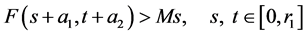
因此 ,其中
,其中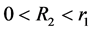 ,由(H2)可得
,由(H2)可得

取定足够大的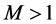 ,满足
,满足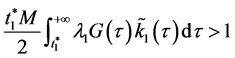 ,可得
,可得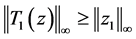
同理可证明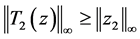 。所以
。所以
引理3.5:假设(H2)成立,给定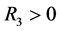 ,存在常数
,存在常数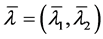 且
且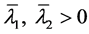 ,则对任意的
,则对任意的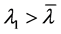 ,
,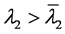 满足下式
满足下式
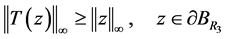
证明: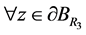 ,有
,有
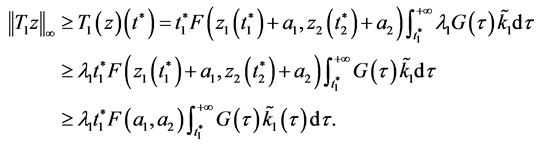
选择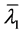 满足
满足

同理可取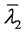 满足
满足

则引理得到证明。
定理1.1的证明:有定理(2.1),引理(3.3)和引理(3.4)可知,![]() 有一个不动点
有一个不动点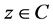 ,且
,且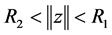 。
。
定理1.2的证明:令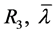 是引理(3.5)中取定的
是引理(3.5)中取定的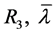 ,给定
,给定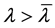 ,既
,既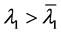 ,
,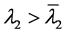 ,取定
,取定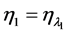 ,
, 满足
满足
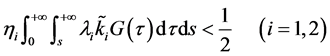
由(H3),可取到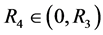 满足
满足
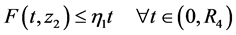
因此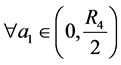 ,
,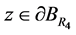 有下式成立
有下式成立

所以
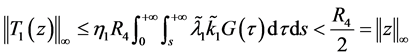
同理可证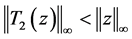 ,既得
,既得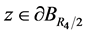
 。
。
结合引理3.3和引理3.4,选定 满足
满足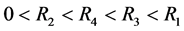 ,则知
,则知![]() 有三个不动点
有三个不动点 且满足
且满足
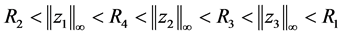
即定理1.2得到证明。
基金项目
沪江基金(B14005)资助。
参考文献 (References)
- [1] Do, O.J.M., Lorcab, S. and Ubillac, P. (2005) Three positive radial solutions for elliptic equations in a ball. Applied Mathematics Letters, 18, 1163-1169.
- [2] Ambrosetti, A. and Colorado, E. (2006) Bound and ground states of coupled nonlinear Schrodinger equations. Comptes Rendus de l’Académie des Sciences—Series I, 342, 453-458.
- [3] Ambrosetti, A., Colorado, E. and Ruiz, D. (2007) Multi-bumb solitons to linearly coupled systems of nonlinear Schrodinger equations. Calculus of Variations and Partial Differential Equations, 30, 85-112.
- [4] Ambrosetti, A. and Colorado, E. (2007) Standing waves of some coupled nonlinear Schrodinger equations. Journal London Mathematical Society, 75, 67-82.
- [5] Torres, P.J. (2006) Guided waves in a multi-layered optical structure. Nonlinearity, 19, 2103-2113.
- [6] Chu, J., O’regan, D. and Zhang, M. (2007) Positive solutions and eigenvalue intervals for nonlinear systems. Proceedings Mathematical Sciences, 117, 85-95.
- [7] Krasnoselskii, M.A. (1964) Positive solutions of operator equation. Noordhoff, Groningen.
- [8] Granas, A. and Dugundji, J. (2003) Fixed point theory. Springer, Berlin.
- [9] Jiang, D., Wei, J. and Zhang, B. (2002) Positive periodic solutions of functional differential equations and population models. Electronic Journal of Differential Equations, 71, 1-13.
- [10] Belmonte-Beitia, J., Perez-Garcia, V.M. and Torres, P.J. (2009) Solitary waves for linearly coupled nonlinear Schrodinger equations with inhomogeneous coefficients. Journal of Nonlinear Science, 19, 437-451.