Pure Mathematics
Vol.06 No.01(2016), Article ID:16846,8
pages
10.12677/PM.2016.61007
Least Squares Hermitian Solution of Complex Matrix Equation AXB = C
Peng Wang, Jianbo Chen
School of Mathematics and Computational Science, Wuyi University, Jiangmen Guangdong

Received: Dec. 23rd, 2015; accepted: Jan. 23rd, 2016; published: Jan. 28th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Based on Moore-Penrose generalized inverse, by making use of matrix-vector production, an analytical expression of the least-squares Hermitian solution with the minimum-norm of complex matrix equation AXB = C is derived.
Keywords:Matrix Equation, Least-Square Solution, Moore-Penrose Inverse Generalized, Hermitian Solution

复矩阵方程AXB = C的最小二乘Hermite解
王 鹏,陈剑波
五邑大学数学与计算科学学院,广东 江门

收稿日期:2015年12月23日;录用日期:2016年1月23日;发布日期:2016年1月28日

摘 要
本文利用Moore-Penrose广义逆的方法,探讨了复矩阵方程的最小二乘Hermitian解,推到出了该类方程最小范数约束的最小二乘Hermitian解的解析形式。
关键词 :矩阵方程,最小二乘解,Moore-Penrose广义逆,Hermitian解

1. 问题简述
首先给出本文采用的一些记号, ,分别用了表示实值列向量集合,
,分别用了表示实值列向量集合, 实值矩阵集合,
实值矩阵集合, 的实对称矩阵集合,
的实对称矩阵集合, 的实值反对称矩阵集合,
的实值反对称矩阵集合, 的复值矩阵集合和
的复值矩阵集合和 的Hermitian矩阵集合。对于任意的Hermitian矩阵
的Hermitian矩阵集合。对于任意的Hermitian矩阵 其转置矩阵,共轭转置矩阵和Moor-Penrose广义逆分别表示为:
其转置矩阵,共轭转置矩阵和Moor-Penrose广义逆分别表示为: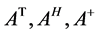 。线性内积空间
。线性内积空间 中任意两个元素的内积定义为:
中任意两个元素的内积定义为:

该内积空间中的范数定义为:

其中: 表示A的Frobenius范数。
表示A的Frobenius范数。
本文主要考虑以下问题:
问题一:
对任意的矩阵: 设
设
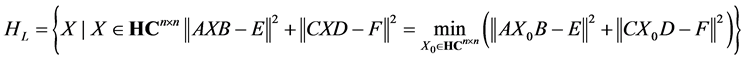 (1.1)
(1.1)
求满足: 并且
并且 的解。
的解。
问题一的解 被称为复矩阵方程
被称为复矩阵方程
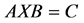 (1.2)
(1.2)
的带有最小范数约束的最小二乘Hermitian解。
由于矩阵方程在工程领域尤其是控制领域有着极其广泛的应用,近年来,矩阵方程的求解问题一直是一个非常热门的研究领域,比如:运用广义奇异值分解和标准相关分解相结合,廖安平教授[1] 给出了一类矩阵方程的求解方法,袁世芳教授[2] -[4] 以Kronecker积为工具,推到了一类矩阵方程的带有最小范数约束的最小二乘解。其他更多的研究方法可以参考文献[5] -[12] 。
然而,已有的方法大多是关于实矩阵方程的,他们的方法很难直接用于复矩阵方程的Hermitian解的问题中,本文通过定义一种新的矩阵和向量的运算,将问题一的求解转化成一类实矩阵方程的求解问题,给出了一个一般的解析解形式,并用具体的数值计算验证了该解析解的正确性。
2. Hilbert内积空间 中的一类最小二乘解问题
中的一类最小二乘解问题
设: ,若矩阵方程
,若矩阵方程 是不相容的,线性最小二乘问题就是求解一个满足
是不相容的,线性最小二乘问题就是求解一个满足 的向量
的向量 ,该问题的解可以通过求解其正则方程得到:
,该问题的解可以通过求解其正则方程得到:
 (2.1)
(2.1)
特别地,当矩阵方程 相容的时候,其正则方程也是相容的,并且二者的解也是一样的。根据这一重要结论,我们给出如下问题:
相容的时候,其正则方程也是相容的,并且二者的解也是一样的。根据这一重要结论,我们给出如下问题:
问题二:对复矩阵 ,以及
,以及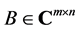 求向量
求向量 使其满足:
使其满足:
 (2.2)
(2.2)
定理2.1:若问题二中的方程(2.2)是相容的,设:

则方程组(2.2)和下列方程组是同解方程组:
 (2.3)
(2.3)
证明:


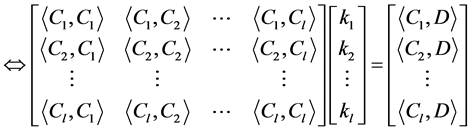 .
.
定理2.1得证。
在问题二中,如果方程(2.2)是不相容的,就需要讨论它相应的最小二乘解。
问题三:对复矩阵 以及
以及 求向量
求向量 使其满足:
使其满足:
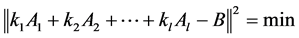
如下定理将问题三的最小二乘解问题转化成相容的矩阵方程组的求解问题:
定理2.2:仍然沿用定理2.1的所有记号,并且定理2.1条件也都满足,则问题三和方程组(2.3)同解。
证明:

从而,命题得证。
3. 表达式 在
在 空间上的结构形式
空间上的结构形式
为了给出 在空间
在空间 上的结构,我们首先定义一种在空间
上的结构,我们首先定义一种在空间 上的矩阵与向量的乘积。
上的矩阵与向量的乘积。
定义1:设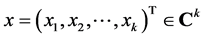 ,
,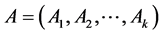 ,
, ,
, 。则定义如下乘积:
。则定义如下乘积:
1) ;
;
2) 
对任意的 ,因为
,因为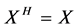 ,即
,即 ,从而可得
,从而可得 ,
, 。
。
定义2:对于实矩阵 ,设
,设
 ,算子
,算子 定义为:
定义为:
 。
。
定义3:对于实矩阵 ,设
,设 ,算子
,算子 定义为:
定义为:
 。
。
设: 其中,
其中,

定义向量 和
和 :
:


我们首先给出如下引理:
引理3.1 设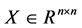 ,则:
,则:
1) 
2) 
引理3.1 设 则
则 。
。
引理3.3 设 。设
。设 ,
, 是矩阵
是矩阵 的第i列,
的第i列, ,
, 是矩阵
是矩阵 的第i列:
的第i列:
 ,
,
其中: ,
,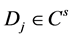 分别是
分别是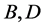 的第j列。
的第j列。
设

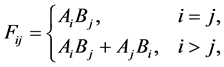
 。
。
证明:由引理3.2可知:

命题得证。
4. 问题一的解的形式
在前面讨论的基础上,本部分内容开始讨论问题一的解,由文献[4] 可知,最小二乘问题

的Hermitian解等价于如下问题:

其中:

从而,我们将求矩阵方程(1.2)的最小二乘约束的解的问题转化为求解一个无约束的实矩阵方程的的求解问题,而该实矩阵方程可以通过Kronecker积和Moore-Penrose广义逆求解[4] 。下面我们运用定理2.2和定理2.4以及引理3.3给出矩阵方程(1.1)的带有最小二乘约束的Hermitian解的求法。
引理4.1 [5] 方程 ,存在一个解当且仅当
,存在一个解当且仅当

并且其通解表达式为:
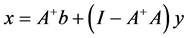
其中: 。
。
引理4.2 [5] 方程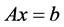 的最小二乘解课表示为
的最小二乘解课表示为
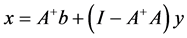
并且,最小范数约束的最小二乘解为: 。
。
为了给出问题一的解,我们首先引入以下几个矩阵:
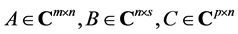 ,设:
,设:
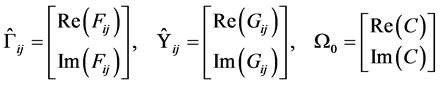 ,
,
 ,其中,
,其中, 。 (4.1)
。 (4.1)

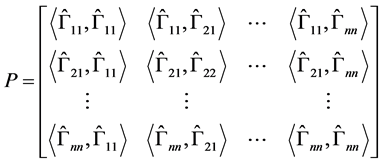


定理4.3 设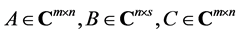 ,并且
,并且 如(4.1)所定义,则:
如(4.1)所定义,则:
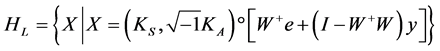 ,
,
其中,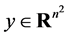 是任意向量。问题一有唯一解
是任意向量。问题一有唯一解 :
:
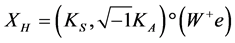 。 (4.2)
。 (4.2)
证明:由引理4.2和定理4.3可知,求最小二乘问题: 的Hermitian解等价于求解:
的Hermitian解等价于求解:

由引理4.1可知:

从而

命题得证。
下面讨论方程(1.2)的解的相容性问题。
设:

其中:


由引理3.3可得:

从而,运用引理4.2和定理4.3可得本文的主要结论:
定理4.4:矩阵方程(1.1)存在一个Herimitian解 当且仅当
当且仅当
 (4.3)
(4.3)
若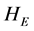 是方程(1.2)的解集,则:
是方程(1.2)的解集,则:

其中: 是任意向量。
是任意向量。
特别地,若(4.3)成立,则方程(1.2)有唯一解 ,当且仅当
,当且仅当 ,此时,
,此时,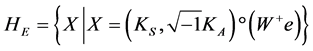 。
。
最小范数问题:

有唯一解 ,并且,
,并且, 可表示为(4.2)。
可表示为(4.2)。
5. 结论
本文主要给出了一类复矩阵方程 的带有Hermitian约束的解析解的存在条件,并以Kronecker积和广义逆为工具,给出了该类方程解的具体形式。
的带有Hermitian约束的解析解的存在条件,并以Kronecker积和广义逆为工具,给出了该类方程解的具体形式。
基金项目
江门市科技计划项目,广东省大学生创新创业项目(1134912031)。
文章引用
王 鹏,陈剑波. 复矩阵方程AXB = C的最小二乘Hermite解
Least Squares Hermitian Solution of Complex Matrix Equation AXB = C[J]. 理论数学, 2016, 06(01): 42-49. http://dx.doi.org/10.12677/PM.2016.61007
参考文献 (References)
- 1. Liao, A.-P. and Lei, Y. (2005) Least Squares Solution with the Mininum-Norm for the Matrix Equation (AXB, GXH) = (C, D). Computers & Mathematics with Applications, 50, 539-549. http://dx.doi.org/10.1016/j.camwa.2005.02.011
- 2. Yuan, Y.-X. (2001) On the Two Classes of Best Approximation Problems. Mathematica Numerica Sinica, 23, 429- 436.
- 3. Yuan, Y.-X. (2002) The Optimal Solution of Linear Matrix Equation by Matrix Decompositions. Mathematica Numerica Sinica, 24, 165-176.
- 4. Yuan, S.-F., Liao, A.-P. and Lei, Y. (2008) Least Squares Hermitian Solution of the Matrix Equation (AXB, CXD) = (E, F) with the Least Norm over the Skew Field of Quaternions. Mathematical and Computer Modelling, 48, 91-100. http://dx.doi.org/10.1016/j.mcm.2007.08.009
- 5. Ben-Israel, A. and Greville, T.N.E. (1974) Generalized Inverses: Theory and Applications. John Wiley and Sons, New York.
- 6. Dehghan, M. and Hajarian, M. (2012) The generalized Sylvester Matrix Equations over the Generalized Bisymmetric and Skew-Symmetric Matrices. International Journal of Systems Science, 43, 1580-1590. http://dx.doi.org/10.1080/00207721.2010.549584
- 7. Krishnaswamy, D. (2011) The Skew-Symmetric Ortho-Symmetric Solutions of the Matrix Equations A^* XA=D. International Journal of Algebra, 5, 1489-1504.
- 8. Sheng, X.-P. and Chen, G.-L. (2010) An Iterative Method for the Symmetric and Skewsymmetric Solutions of a Linear Matrix Equation AXB + CYD = E. Journal of Computational and Applied Mathematics, 233, 3030-3040. http://dx.doi.org/10.1016/j.cam.2009.11.052
- 9. Wang, Q.-W. and He, Z.-H. (2013) Solvability Conditions and General Solution for Mixed Sylvester Equations. Automatica, 49, 2713-2719. http://dx.doi.org/10.1016/j.automatica.2013.06.009
- 10. Xiao, Q.F. (2012) The Hermitian R-Symmetric Solutions of the Matrix Equation AXA^*=B. International Journal of Algebra, 6, 903-911.
- 11. Farid, F.O., Moslehian, M.S., Wang, Q.W. and Wu, Z.C. (2012) On the Hermitian Solutions to a System of Adjointable Operator Equations. Linear Algebra and Its Applications, 437, 1854-1891. http://dx.doi.org/10.1016/j.laa.2012.05.012
- 12. Dong, C.Z., Wang, Q.W. and Zhang, Y.P. (2012) The Common Positive Solution to Adjointable Operators Equations with an Application. Journal of Mathematical Analysis and Applications, 396, 670-679. http://dx.doi.org/10.1016/j.jmaa.2012.07.001