Pure Mathematics
Vol.06 No.04(2016), Article ID:18152,19
pages
10.12677/PM.2016.64050
The Compatibility of Two Free Boundary Problem of Euler Equation
Xiaoqing Wu
College of Science, Southwest Petroleum University, Chengdu Sichuan

Received: Jul. 9th, 2016; accepted: Jul. 26th, 2016; published: Jul. 29th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we model the free boundary problem of the Perpetual American Option as boundary value problem with multiple (or single) singular points in the semi infinite domain, and introduce the generalized characteristic function method to be able to obtain the exact solution of the mathematical model of multiple singular point. In the single singular point case, our solution function takes the maximum value at the singular point. We deduce the consistency condition of the left and right free boundary problem. Under the compatibility condition, the three points, the left and right free boundary points and singular point are the same, so that they all are the optimal implementation point of the Perpetual American Option. In the case of multiple singular points, the conditional judgment of the left and right free boundary points to be the optimal or nearly optimal implementation point is obtained.
Keywords:Permanent American Option, Optimal Exercise Boundary, Free Boundary Problem, Singular Point, Generalized Characteristic Function Method

尤拉方程的两个自由边界问题的相容性
吴小庆
西南石油大学理学院,四川 成都

收稿日期:2016年7月9日;录用日期:2016年7月26日;发布日期:2016年7月29日

摘 要
本文将永久美式期权的自由边界问题归结为在半无界区域具有多个(或单个)奇异点的边值问题来研究,引入广义特征函数法获得了多个奇异点的数学模型的精确解。只有一个奇异点的情形,所得到的解函数在奇异点处取最大值;并得到了左、右自由边界问题同时有一致解的相容性条件。证明了在相容性条件下,左、右自由边界点与奇异点三点合一,从而左、右自由边界点与奇异点都是永久美式期权最佳实施边界点。具有多个奇异点的情形,获得了判断左、右自由边界点成为最佳或较佳实施边界点的条件。
关键词 :永久美式期权,最佳实施边界,自由边界问题,奇异点,广义特征函数法

1. 引言
美式期权是一张具有提前实施条款的合约,由于可以提前实施,持有者能否抓住有利时机,适时地实施这张合约,以获取最大或较大利益,这是一个对持有者必须考虑的问题。在研究永久美式期权 [1] - [3] 确定最佳实施边界的问题是齐次尤拉方程的自由边界问题 [1] 。永久美式期权的期权价格函数与时间无关,它是原生资产价格 的函数,记为
的函数,记为 。期权价格函数
。期权价格函数 在半无界区域满足齐次尤拉方程,寻求最佳实施边界
在半无界区域满足齐次尤拉方程,寻求最佳实施边界 的问题是把半无界区域分成
的问题是把半无界区域分成 和
和 两部分,持有者在
两部分,持有者在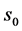 实施这张合约,其目的是获取最大的收益,使得期权价格函数达到最大值。寻求最佳实施边界
实施这张合约,其目的是获取最大的收益,使得期权价格函数达到最大值。寻求最佳实施边界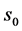 会产生两个自由边界问题 [1] :
会产生两个自由边界问题 [1] :
自由边界问题A:求 使得
使得

且满足 ;
;
自由边界问题B:求 使得
使得
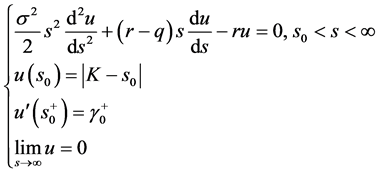
且满足 。
。
我们把自由边界问题A与自由边界问题B分别称为左、右自由边界问题。由左自由边界问题或右自由边界问题去确定最佳实施边界点 。如果同时考虑左、右两个自由边界问题,所得到的自由边界点
。如果同时考虑左、右两个自由边界问题,所得到的自由边界点 是否一致?两个自由边界问题的自由边界点
是否一致?两个自由边界问题的自由边界点 相同的条件是什么?左自由边界点
相同的条件是什么?左自由边界点 与右自由边界点
与右自由边界点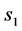 如果不相同,这两个自由边界点中哪个是最佳实施边界点?本文将上述问题归结为在半无界区域具有多个(或单个)奇异点的边值问题来研究。该边值问题的解称为弱解,它在半无界区域连续,但解的导数在奇异点处发生间断。该边值问题需同时求满足问题的解和它的奇异点。本文引入广义特征函数法获得了多个奇异点的数学模型的精确解,应用该结果对左、右自由边界问题进行了深入的研究。在只有一个奇异点的情形,所得到的解在奇异点处取最大值;得到了左、右自由边界问题同时有一致解的相容条件;证明了在相容条件下,左、右自由边界点与奇异点三点合一,从而左、右自由边界点与奇异点都是永久美式期权最佳实施边界点。具有多个奇异点
如果不相同,这两个自由边界点中哪个是最佳实施边界点?本文将上述问题归结为在半无界区域具有多个(或单个)奇异点的边值问题来研究。该边值问题的解称为弱解,它在半无界区域连续,但解的导数在奇异点处发生间断。该边值问题需同时求满足问题的解和它的奇异点。本文引入广义特征函数法获得了多个奇异点的数学模型的精确解,应用该结果对左、右自由边界问题进行了深入的研究。在只有一个奇异点的情形,所得到的解在奇异点处取最大值;得到了左、右自由边界问题同时有一致解的相容条件;证明了在相容条件下,左、右自由边界点与奇异点三点合一,从而左、右自由边界点与奇异点都是永久美式期权最佳实施边界点。具有多个奇异点 的情形,左自由边界问题的自由边界
的情形,左自由边界问题的自由边界 是最小的奇异点,右自由边界问题的自由边界
是最小的奇异点,右自由边界问题的自由边界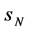 是最大的奇异点,获得了判断左、右自由边界点成为最佳或较佳实施边界点的条件。
是最大的奇异点,获得了判断左、右自由边界点成为最佳或较佳实施边界点的条件。
2. 主要结果
2.1. 两个奇异点的数学模型
记号 ,
,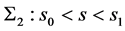 ,
, ,
, ,
, ,
,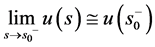 ,
, ,
, ,
,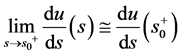 。
。
问题1 (两个奇异点的数学模型)求 使其满足
使其满足
 (1)
(1)
其中: 是区域
是区域 内的非负连续函数。
内的非负连续函数。
定义1若函数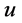 在区域
在区域 内连续有界,但
内连续有界,但 在
在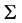 内的某点
内的某点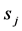 一阶左、右导数
一阶左、右导数 ,则称
,则称 为函数
为函数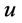 的奇异点。
的奇异点。
定义2在区域 内具有多个(或单个)奇异点的数学模型的解称为弱解;弱解是区域
内具有多个(或单个)奇异点的数学模型的解称为弱解;弱解是区域 内的连续有界正解。
内的连续有界正解。
问题1的求解需同时求解(弱解) 和其奇异点
和其奇异点 。
。
问题1的求解:
齐次尤拉方程有形如 的特解,将其代入尤拉方程,得到特征方程
的特解,将其代入尤拉方程,得到特征方程
 (2)
(2)
它有两个根,记为
 (3)
(3)
其中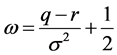 。
。
易知
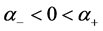 (4)
(4)
故方程的通解为
 (5)
(5)
其中 为任意常数。由边界条件
为任意常数。由边界条件 推岀
推岀 ,由边界条件
,由边界条件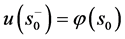 得到
得到 ,从而
,从而
 (6)
(6)
由(6)和边界条件, 得到
得到
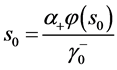 (7)
(7)
完全类似的,得到
 (8)
(8)
 (9)
(9)
再求

由边界条件
有

这是关于 的非齐次线性方程组,由克莱姆法则即得
的非齐次线性方程组,由克莱姆法则即得

于是有
 (10)
(10)
由条件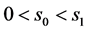 和正解条件,必须要求
和正解条件,必须要求
 (11)
(11)
定理1 (问题1连续有界正解的存在定理)当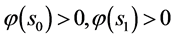 ,
, 时,问题1的解存在唯一,且可表出
时,问题1的解存在唯一,且可表出
 (12)
(12)
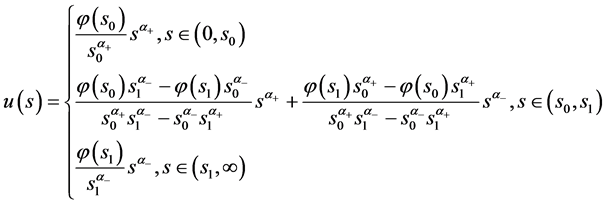 (13)
(13)
或 (14)
(14)
定理2 (问题1连续有界正解性质定理)问题1连续有界正解 ;有
;有 ,
,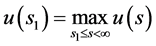 。
。
证明:由问题1的解在区间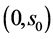 中的表达式:
中的表达式: ,有
,有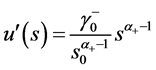 ,又
,又 ,
, 在区间
在区间 中
中 ,
, 单调增加,故
单调增加,故 :
:
由问题1的解在区间 的表达式:
的表达式: ,有
,有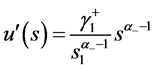 ,又
,又 ,
, 在区间
在区间 中
中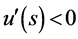 ,
,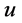 单调减少,故
单调减少,故 。
。
定义3若函数 ;在区域
;在区域 内点
内点 处取最大值
处取最大值 ,则称点
,则称点 为函数
为函数 的最佳实施边界,简称最佳实施点。
的最佳实施边界,简称最佳实施点。
定理3 (问题1连续有界正解最佳实施点排除定理)若 ,问题1连续有界正解
,问题1连续有界正解 ,则
,则
1) 当 时,奇异点
时,奇异点 不是最佳实施点;
不是最佳实施点;
2) 当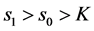 时,奇异点
时,奇异点 不是最佳实施点;
不是最佳实施点;
3) 当 时,奇异点
时,奇异点 不是最佳实施点;当
不是最佳实施点;当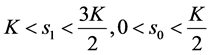 ,奇异点
,奇异点 不是最佳实施点。
不是最佳实施点。
证明:由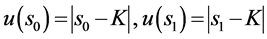 易知,当
易知,当 时,
时, ,
, ,
, ,
,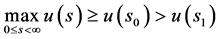 ,
, 不是在区域
不是在区域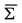 的最大值,从而
的最大值,从而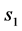 点不是最佳实施点。
点不是最佳实施点。
当 时,
时, ,
,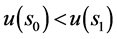
 ,
,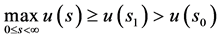 ,
,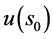 不是在区域
不是在区域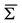 的最大值,
的最大值, 点不是最佳实施点。当
点不是最佳实施点。当 ,
, 时,
时, ,
, ,
, ,有
,有 ,
, 点不是最佳实施点;当
点不是最佳实施点;当 时,
时, 有
有 ,
,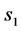 点不是最佳实施点。
点不是最佳实施点。
即一般情况下两个奇异点 不一定是最佳实施点。
不一定是最佳实施点。
推论1若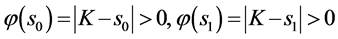 ,则问题1的连续有界正解
,则问题1的连续有界正解
 (15)
(15)
且
1) 当且仅当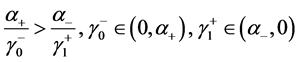 ,有
,有
 (16)
(16)
2) 当且仅当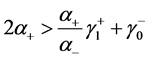 ,
, ,有
,有
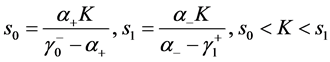 (17)
(17)
3) 当且仅当 ,
, ,有
,有
 (18)
(18)
证明由(12),(13)易得。
问题2.1求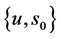 使得
使得
 (19)
(19)
问题2.2求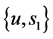 使得
使得
 (20)
(20)
问题2.3求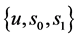 使得
使得
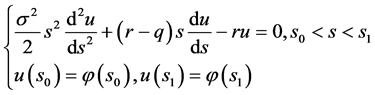 (21)
(21)
推论2当 时,问题2.1,问题2.2与问题2.3三个自由边界问题都有解,问题2.1的解
时,问题2.1,问题2.2与问题2.3三个自由边界问题都有解,问题2.1的解
 (22)
(22)
问题2.2的解
 (23)
(23)
问题2.3的解
 (24)
(24)
且有 。
。
定义4称问题2.1为左自由边界问题,它的自由边界 称为左自由边界点;称问题2.2为右自由边界问题,其自由边界
称为左自由边界点;称问题2.2为右自由边界问题,其自由边界 称为右自由边界点。
称为右自由边界点。
推论3若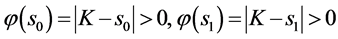 ,左、右自由边界问题都有解。左自由边界问题的解
,左、右自由边界问题都有解。左自由边界问题的解
 且满足
且满足
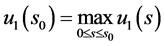 (25)
(25)
1) 当
 ,
, (26)
(26)
2) 当
 ,
, (27)
(27)
右自由边界问题的解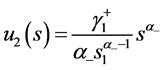 ,且满足
,且满足
 (28)
(28)
1) 当
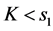 ,
, (29)
(29)
2) 当
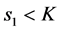 ,
, (30)
(30)
定义5 左自由边界点 ,右自由边界点
,右自由边界点 ,若有
,若有 ,则称右自由边界点
,则称右自由边界点 比左自由边界点
比左自由边界点 优,称右自由边界点
优,称右自由边界点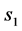 为较佳实施边界点:若有
为较佳实施边界点:若有 ,则称左自由边界点
,则称左自由边界点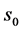 比右自由边界点
比右自由边界点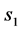 优,称左自由边界点
优,称左自由边界点 为较佳实施边界点。
为较佳实施边界点。
推论4若 ,则左、右自由边界问题都有解,
,则左、右自由边界问题都有解,
 ,
,
且
1) 当且仅当 ,有
,有
 (31)
(31)
2) 当且仅当 ,有
,有
 (32)
(32)
3) 当且仅当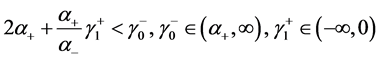 ,有
,有
 (33)
(33)
推论5若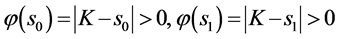 ,则左、右自由边界问题都有解。此时
,则左、右自由边界问题都有解。此时
 ,且
,且
1) 当且仅当 ,
, ,
,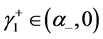 ,有
,有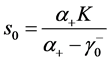 ,
, ,
, ,
,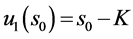 ,
, ,
, 。
。
2) 当且仅当 ,
,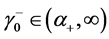 ,
, ,有
,有 ,
,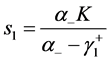 ,
, ,
, ,
, ,
,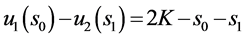 ;若
;若 ,则
,则 ,
, ,有
,有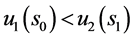 ;若
;若 ,
, ,则
,则 ,
, ,有
,有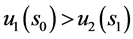 。
。
3)当且仅当 ,
,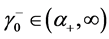 ,
, ,有
,有 ,
, ,
,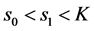 ,
, ,
, ,
, 。
。
证明:由推论4,即有1),3)成立。由推论4有当且仅当 ,
, ,
,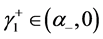 ,有
,有
 ,
, ,
,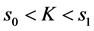 ,
, ,
, ,
,
易证 有
有 ,让
,让 ,则有
,则有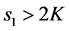 ,从而
,从而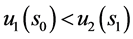 。易证当
。易证当 ,
, ,则有
,则有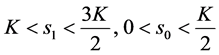 ,从而
,从而 。
。
故2)成立。
推论6设左、右自由边界问题都有解,且左、右自由边界点 ,若左、右自由边界问题的两个解可以连续开拓到
,若左、右自由边界问题的两个解可以连续开拓到 的同一个连续有界函数
的同一个连续有界函数 (即存在连续有界函数
(即存在连续有界函数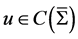 ,满足
,满足 和
和 ),则必有
),则必有 。反之,若左、右自由边界问题都有解,且
。反之,若左、右自由边界问题都有解,且 ,则必存在连续有界函数
,则必存在连续有界函数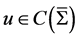 是左、右自由边界问题的解的连续开拓。
是左、右自由边界问题的解的连续开拓。
证明:若存在连续有界函数 ,满足
,满足 和
和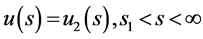 ;则
;则 在区间
在区间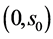 中
中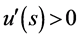 ,
, 单调增加,故
单调增加,故 ;
; 在区间
在区间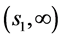 中
中 ,
, 单调减少,故
单调减少,故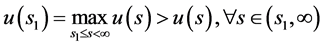 。若
。若 ,则
,则 ,推出
,推出 ;同时
;同时 ,又推出
,又推出 。于是应有两式
。于是应有两式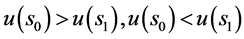 同时成立,矛盾。从而必有
同时成立,矛盾。从而必有 。反之,若左、右自由边界问题都有解,且
。反之,若左、右自由边界问题都有解,且 ,显然存在连续有界函数
,显然存在连续有界函数 是这两个解的连续开拓。
是这两个解的连续开拓。
推论7若左、右自由边界问题都有解,且左、右自由边界点 ,连续有界函数
,连续有界函数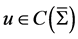 是它们的一个连续开拓,则
是它们的一个连续开拓,则
1) 当 或
或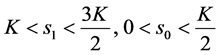 时,左自由边界点
时,左自由边界点 比右自由边界点
比右自由边界点 优。
优。
2) 当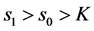 或
或 时,右自由边界点
时,右自由边界点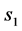 比左自由边界点
比左自由边界点 优。
优。
证明:由定理3即得。
即分别考虑左、右自由边界问题,若左、右两个自由边界点 ,自由边界
,自由边界 或
或 不一定是最佳实施点。
不一定是最佳实施点。
定理4 (自由边界点与最佳实施点关系定理)设左、右自由边界问题都有解,且左、右自由边界点 ,左、右自由边界问题解的连续开拓为
,左、右自由边界问题解的连续开拓为 ,则
,则
1) 若 ,左自由边界点
,左自由边界点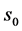 和右自由边界点
和右自由边界点 皆不是该连续开拓
皆不是该连续开拓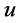 的最佳实施点;当
的最佳实施点;当 ,或
,或 时,左自由边界点
时,左自由边界点 是该连续开拓
是该连续开拓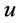 的较佳实施点;当
的较佳实施点;当 ,或
,或 时,右自由边界点
时,右自由边界点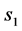 是该连续开拓
是该连续开拓 的较佳实施点。
的较佳实施点。
2) 若 ,当
,当 ,或
,或 时,左自由边界点
时,左自由边界点 是该连续开拓
是该连续开拓 的最佳实施点;当
的最佳实施点;当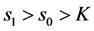 ,或
,或 时,右自由边界点
时,右自由边界点 是该连续开拓
是该连续开拓 的最佳实施点。
的最佳实施点。
下面我们考虑左、右两个自由边界点 的条件。当
的条件。当 ,问题1即演变成单个奇异点的数学模型。
,问题1即演变成单个奇异点的数学模型。
2.2. 单个奇异点的数学模型
问题3 (单个奇异点的数学模型)求 使其满足
使其满足
 (34)
(34)
定理5 (问题3连续有界正解的存在定理)当 ,
,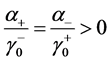 时,问题3的解存在唯一,且可表出
时,问题3的解存在唯一,且可表出
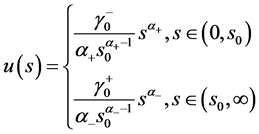 ,
,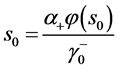 (35)
(35)
定义6函数 在
在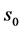 点一阶左,右导数之差
点一阶左,右导数之差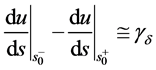 ,称
,称 为
为 在
在 点的跳跃度。
点的跳跃度。
我们已在 [4] 中得到 ,
,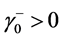 ,
, 三者中任一个确定其它两个;问题3连续有界正解也可由
三者中任一个确定其它两个;问题3连续有界正解也可由 表示,即有
表示,即有
定理6 (问题3连续有界正解的不同表示定理)当 ,
,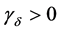 ,问题3连续有界正解存在,且有精确解的表达式
,问题3连续有界正解存在,且有精确解的表达式
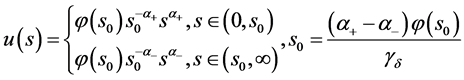 (36)
(36)
或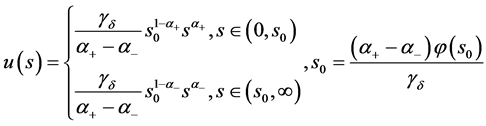 (37)
(37)
定理7 (问题3连续有界正解性质定理)问题3连续有界正解

且解在奇异点 处取正的最大值
处取正的最大值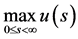 ;奇异点
;奇异点 就是永久美式期权最佳实施边界点。
就是永久美式期权最佳实施边界点。
证明:由(37)式解在区间 中的表达式:
中的表达式: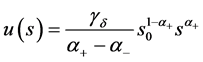 ,有
,有 ,
, 在区间
在区间 中
中 ,
, 单调增加,故
单调增加,故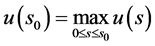 :
:
由(37)式解在区间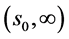 的表达式:
的表达式: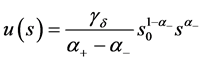 ,有
,有 ,
, 在区间
在区间 中
中 ,
, 单调减少,故
单调减少,故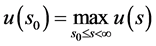 。
。

推论8当 ,
, 时,左、右两自由边界问题都有解,且
时,左、右两自由边界问题都有解,且 ,左自由边界问题的解
,左自由边界问题的解
 (38)
(38)
右自由边界问题的解
 (39)
(39)
定理8 (三点合一定理)当 ,
,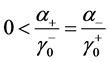 时,左、右两自由边界点都等于奇异点
时,左、右两自由边界点都等于奇异点 ,此时左、右自由边界点
,此时左、右自由边界点 都是永久美式期权最佳实施边界点。
都是永久美式期权最佳实施边界点。
推论9若 ,
, ,则
,则
1) 当 时,有
时,有
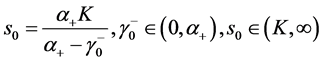 (40)
(40)
2) 当 时,有
时,有
 (41)
(41)
证明:参见 [4] 。
奇异点 和弱解的最大值
和弱解的最大值 构成二维点
构成二维点 ,由
,由 的取值唯一确定。由推论9即知二维点
的取值唯一确定。由推论9即知二维点 所属集合
所属集合
1) 当 时,
时, ;
;
2) 当 时,
时, 。
。
推论10问题3 (单个奇异点的数学模型)与 [4] 中问题2 (单个奇异点的基本解数学模型)是等价的。
证明:参见 [4] 中在广义函数空间关于基本解的推导即得。
从而研究问题3 (单个奇异点的数学模型)与 [4] 中问题2所得结果完全一致。
2.3. 求解多个奇异点的数学模型的特征函数法
问题4 (多个奇异点的数学模型)
 (42)
(42)
其中: 为狄拉克d-函数,
为狄拉克d-函数,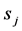 为奇异点,
为奇异点, ,
, 。
。
等价于标准形式
 (43)
(43)
其中: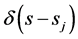 为狄拉克d-函数,
为狄拉克d-函数, 为奇异点,
为奇异点, ,
, ;
;
微分算子
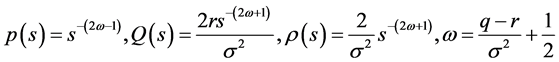
问题4的求解:
先考虑特征值问题
 (44)
(44)
这是关于尤拉方程在半无界区间的奇异施图姆-刘维尔问题。
尤拉方程的特解形式为 ,代入方程即有
,代入方程即有
特征根

即有

于是得到特征值
 (45)
(45)
特征函数
 (46)
(46)
特征函数系是半无界区域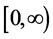 上带权函数
上带权函数 的完备正交系。由于
的完备正交系。由于

即知特征函数系是半无界区域 上带权函数
上带权函数 的正交系。正交关系
的正交系。正交关系
 (47)
(47)
定义在 的连续函数
的连续函数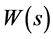 可以展为特征函数的积分形式
可以展为特征函数的积分形式
 (48)
(48)
由正交关系

 (49)
(49)
由(48),(49)这一对关系可以引入广义特征函数法 [5] 求解问题4。由(48)将问题4的解表为
 (50)
(50)
由(49)则有
 (51)
(51)
 (52)
(52)

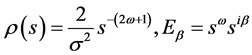

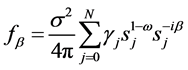 (53)
(53)
 (54)
(54)
将(53),(54)两式代入(43)中方程则有

于是
 (55)
(55)
 (56)
(56)
将上式代入(50)式即有
 (57)
(57)
再将(45),(46),(53)式代入(57)式
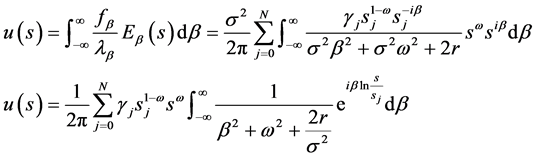
由傅立叶积分变换公式
即知 (59)
(59)
定理9若 ,
, ,则问题4的精确解为
,则问题4的精确解为
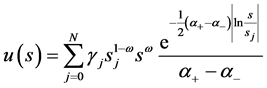 (60)
(60)
若该解还满足内边界条件
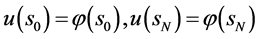 (61)
(61)
则应有相容条件
 (62)
(62)
 (63)
(63)
记
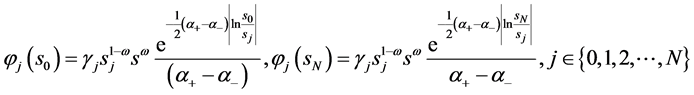
则有
 (64)
(64)
 (65)
(65)
附注1定理9中条件 即知,(60)式表示的不一定是正解,若在条件
即知,(60)式表示的不一定是正解,若在条件 下,则一定是正解。
下,则一定是正解。
问题5 (多个奇异点的数学模型)求 使得
使得

记号
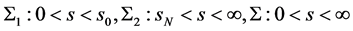
定理10当 ,且
,且 ,满足条件
,满足条件
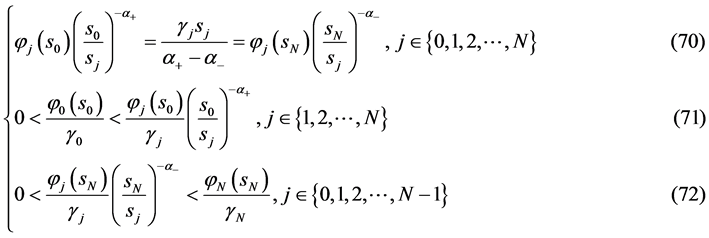
则问题5存在连续有界正解 ,且可表为
,且可表为
 (73)
(73)
证明由问题4的解,记为
 (74)
(74)
则 满足问题5中(66),(69)两式,由(71),(72),(73)三式即有
满足问题5中(66),(69)两式,由(71),(72),(73)三式即有 ,且
,且
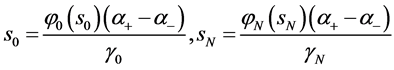 (75)
(75)
1) 
由 ,有
,有 ,
,
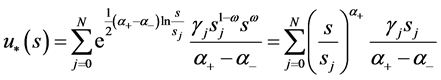 (76)
(76)
 (77)
(77)
 (78)
(78)
 (79)
(79)
由(71),(72),(73)三式即有
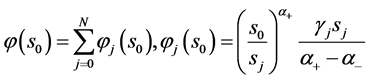 (80)
(80)
从而 (81)
(81)
2) 
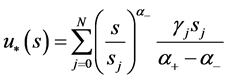 (82)
(82)
 (83)
(83)
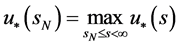 (84)
(84)
由(82)有
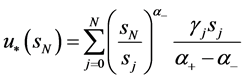 (85)
(85)
由(71),(72),(73)三式即有
 (86)
(86)
即有
 (87)
(87)
由(81),(87)两式即 满足条件(67)和(68),为问题5的解。
满足条件(67)和(68),为问题5的解。
左自由边界问题5.1求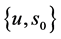 使得
使得
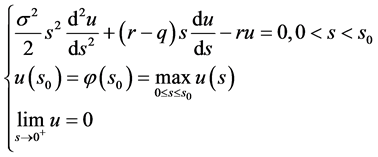 (88)
(88)
定理11当 ,且
,且 ,满足条件
,满足条件
 (89)
(89)
则左自由边界问题5.1存在连续有界正解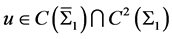 ,且可表为
,且可表为
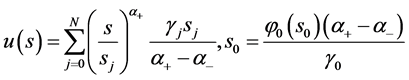 (90)
(90)
且满足
 (91)
(91)
推论11当自由边界问题2.1中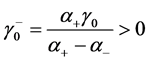 ,
, ,则存在连续有界正解
,则存在连续有界正解 ,且可表为
,且可表为
 (92)
(92)
右自由边界问题5.2求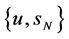 使得
使得
 (93)
(93)
定理12当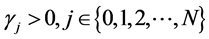 ,且
,且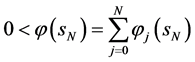 ,满足条件
,满足条件
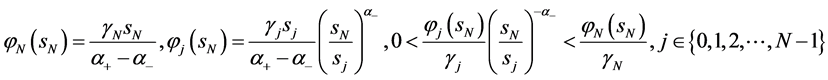 (94)
(94)
则右自由边界问题5.2存在连续有界正解 ,且可表为
,且可表为
 (95)
(95)
且满足
 (96)
(96)
推论12当自由边界问题2.2中 ,则存在连续有界正解
,则存在连续有界正解 ,且可表为
,且可表为
 (97)
(97)
附注2问题5连续有界正解 ,
, ,
, ,
, 。问题5连续有界正解是左自由边界问题题5.1与右自由边界问题5.2的解的连续开拓,若
。问题5连续有界正解是左自由边界问题题5.1与右自由边界问题5.2的解的连续开拓,若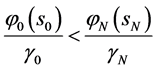 ,则有左、右两个自由边界点
,则有左、右两个自由边界点 ,自由边界
,自由边界 或
或 不一定是最佳实施点。
不一定是最佳实施点。
附注3由定理11与推论11的结论可知,左自由边界问题5.1与左自由边界问题2.1有差异很大的解。由定理12与推论12的结论可知,右自由边界问题5.2与右自由边界问题2.2也有差异很大的解。
3. 结论
I简单期权价格曲线的情形,即期权价格曲线在区域 内有且仅有一个奇异点
内有且仅有一个奇异点 的情形。问题3的研究得到期权价格函数
的情形。问题3的研究得到期权价格函数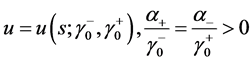 依赖于
依赖于 的取值,不同的
的取值,不同的 的取值得到不同的期权价格曲线,实际上我们得了简单期权价格曲线族
的取值得到不同的期权价格曲线,实际上我们得了简单期权价格曲线族 。简单期权价格曲线的情形,由定理8 (三点合一定理),左、右自由边界点与奇异点三点合一,左、右自由边界点与弱间断点都是永久美式期权最佳实施边界点。奇异点
。简单期权价格曲线的情形,由定理8 (三点合一定理),左、右自由边界点与奇异点三点合一,左、右自由边界点与弱间断点都是永久美式期权最佳实施边界点。奇异点 的判定:期权价格函数
的判定:期权价格函数 在该点左、右导数由正变负,即
在该点左、右导数由正变负,即 ,
, 。对期权价格曲线族而言,奇异点
。对期权价格曲线族而言,奇异点 的取值可以很小,也可以很大,它分布在半无穷区间
的取值可以很小,也可以很大,它分布在半无穷区间 上。具体的期权价格曲线奇异点
上。具体的期权价格曲线奇异点 的确定依赖于该期权价格曲线的运行趋势,依赖于期权价格曲线在
的确定依赖于该期权价格曲线的运行趋势,依赖于期权价格曲线在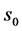 点的跳跃度
点的跳跃度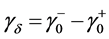 。对于简单期权价格曲线而言,确定跳跃度的取值是计祘永久美式期权最佳实施边界点的一条途径。
。对于简单期权价格曲线而言,确定跳跃度的取值是计祘永久美式期权最佳实施边界点的一条途径。
II复杂期权价格曲线的情形,即期权价格函数曲线在区域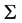 内具有多个奇异点
内具有多个奇异点 的情形,左自由边界问题的自由边界
的情形,左自由边界问题的自由边界 为最小的奇异点,右自由边界问题的自由边界
为最小的奇异点,右自由边界问题的自由边界 为最大的奇异点。当
为最大的奇异点。当 或
或 时,左自由边界点
时,左自由边界点 比右自由边界点
比右自由边界点 优,较佳实施边界点为
优,较佳实施边界点为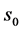 ;当
;当 或
或 时,右自由边界点
时,右自由边界点 比左自由边界点
比左自由边界点 优,较佳实施边界点为
优,较佳实施边界点为 。即在不同情况下,由定理4 (自由边界点与最佳实施点关系定理)即知,考虑左、右两自由边界问题,一般不能断定自由边界
。即在不同情况下,由定理4 (自由边界点与最佳实施点关系定理)即知,考虑左、右两自由边界问题,一般不能断定自由边界 与
与 是否是永久美式期权最佳实施边界点。在复杂多变的情况下,一般不能用左、右两自由边界问题所得到的自由边界点
是否是永久美式期权最佳实施边界点。在复杂多变的情况下,一般不能用左、右两自由边界问题所得到的自由边界点 的计祘结果去断定其为永久美式期权最佳实施边界点。单独考虑左或右自由边界问题所得到的自由边界点的计祘结果皆有可能与真实情况的最佳实施边界点相差很远。
的计祘结果去断定其为永久美式期权最佳实施边界点。单独考虑左或右自由边界问题所得到的自由边界点的计祘结果皆有可能与真实情况的最佳实施边界点相差很远。
文章引用
吴小庆. 尤拉方程的两个自由边界问题的相容性
The Compatibility of Two Free Boundary Problem of Euler Equation[J]. 理论数学, 2016, 06(04): 342-360. http://dx.doi.org/10.12677/PM.2016.64050
参考文献 (References)