Pure Mathematics
Vol.06 No.05(2016), Article ID:18608,4
pages
10.12677/PM.2016.65059
Finitely Generated Torsion-Free Nilpotent Groups Admitting an Automorphism of Order Four
Xiaodi Ma1, Tao Xu2*
1College of Computer Science and Technology, Nanjing University of Science and Technology, Nanjing Jiangsu
2College of Science, Hebei University of Engineering, Handan Hebei

Received: Sep. 3rd, 2016; accepted: Sep. 19th, 2016; published: Sep. 26th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Let G be a finitely generated torsion-free nilpotent group and a an automorphism of order four of G. If the map 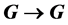 defined by
defined by  is surjective, then the second derived subgroup
is surjective, then the second derived subgroup  is included in the centre of G and
is included in the centre of G and  is abelian.
is abelian.
Keywords:Finitely Generated, Torsion-Free Nilpotent Group, Regular Automorphism, Automorphism

有限生成无挠幂零群的4阶自同构
马晓迪1,徐涛2*
1南京理工大学计算机科学与工程学院,江苏 南京
2河北工程大学理学院,河北 邯郸

收稿日期:2016年9月3日;录用日期:2016年9月19日;发布日期:2016年9月26日

摘 要
设G是有限生成无挠幂零群,a是G的4阶自同构且 是满射,则G的二阶导群
是满射,则G的二阶导群 包含在G的中心
包含在G的中心 里且
里且 是Abel群。
是Abel群。
关键词 :有限生成,无挠幂零群,正则自同构,自同构

1. 引言和主要结果
本文采用的符号和术语都是标准的,按照 [1] 。
在群论里,如果群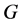 的自同构
的自同构 没有非平凡的不动点,则称
没有非平凡的不动点,则称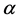 是正则自同构。
是正则自同构。
对于2阶正则自同构,Burnside [2] 证明了一个经典结果。即
命题1.1 设 是有限群,
是有限群,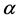 是
是 的2阶正则自同构当且仅当
的2阶正则自同构当且仅当 是奇阶Abel群。
是奇阶Abel群。
对于3阶正则自同构,Gorenstein [3] 证明了具有3阶正则自同构的有限群是幂零群。Neumann [4] 把有限群推广到任意群,得到了下面的结果。
命题1.2 设 是一个群,
是一个群, 是
是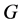 的3阶正则自同构且
的3阶正则自同构且 是满射,则
是满射,则 是幂零类不超过2的幂零群。
是幂零类不超过2的幂零群。
对于素数阶正则自同构,Thompson [5] 证明了有限群论里的一个著名结果:如果有限群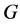 有一个素数阶的正则自同构,那么
有一个素数阶的正则自同构,那么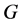 是幂零群。在无限群中,Higman [6] 用Lie环的方法证明了:如果局部幂零群
是幂零群。在无限群中,Higman [6] 用Lie环的方法证明了:如果局部幂零群 具有素数
具有素数 阶的正则自同构,那么
阶的正则自同构,那么 是幂零类不超过
是幂零类不超过 的幂零群,其中
的幂零群,其中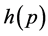 是只与
是只与 有关的函数。在 [7] 中,我们推广了Higman的结果,用纯群论的方法证明了下面的结论。
有关的函数。在 [7] 中,我们推广了Higman的结果,用纯群论的方法证明了下面的结论。
命题1.3 设 是剩余有限的可解群或是剩余有限的可解群的有限扩张,
是剩余有限的可解群或是剩余有限的可解群的有限扩张,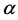 是
是 的素数
的素数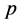 阶正则自同构且
阶正则自同构且 是满射,则
是满射,则 是幂零类不超过
是幂零类不超过 的幂零群,其中
的幂零群,其中 是只与
是只与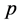 有关的函数。
有关的函数。
受命题1.2和命题1.3的启发,我们舍去自同构正则性的假设,只考虑在满射的条件下,自同构的阶数对群结构的影响。在 [8] 中,我们研究了有限生成无挠幂零群的素数 阶自同构,证明了下面的结果。
阶自同构,证明了下面的结果。
命题1.4 设 是有限生成无挠幂零群,
是有限生成无挠幂零群, 是
是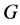 的
的 阶自同构且
阶自同构且 是满射,则
是满射,则 是幂零类不超过
是幂零类不超过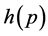 的幂零群,其中
的幂零群,其中 是只与
是只与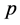 有关的函数。
有关的函数。
在本文中,我们考虑有限生成无挠幂零群的4阶自同构。得到了下面的结果。
定理1.1 设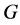 是有限生成无挠幂零群,
是有限生成无挠幂零群, 是
是 的4阶自同构且
的4阶自同构且 是满射,则以下结论成立
是满射,则以下结论成立
(i)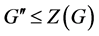 ;
;
(ii) 是Abel群。
是Abel群。
2. 定理的证明
引理2.1 设 是一群,
是一群,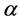 是
是 的
的 阶自同构且
阶自同构且 是满射,则对于任意的
是满射,则对于任意的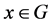 ,有
,有 。
。
证明 因为 是满射,所以对于任意的
是满射,所以对于任意的 ,存在某个
,存在某个 ,使得
,使得 。因此
。因此
 。
。
引理2.2 设 是有限生成无挠幂零群,
是有限生成无挠幂零群, 是
是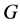 的
的 阶自同构且
阶自同构且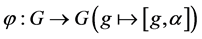 是满射,对于任意的不整除
是满射,对于任意的不整除 的素数
的素数 ,以下结论成立
,以下结论成立
(i) ;
;
(ii) 对于任意的正整数 ,
, 诱导了
诱导了 的正则自同构
的正则自同构 。
。
证明 (i) 由 [1] 的定理
 是剩余有限
是剩余有限 -群。因此对于任意的正整数
-群。因此对于任意的正整数 ,
, 是有限
是有限 -群且
-群且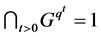 。
。
(ii) 任取 ,使得
,使得 。在
。在 中,我们应用引理2.1可得
中,我们应用引理2.1可得
 。
。
因为 不整除
不整除 ,所以
,所以 。因此
。因此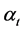 是正则自同构。
是正则自同构。
引理2.3 [9] 设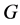 是局部有限群,
是局部有限群, 是
是 的4阶正则自同构,则
的4阶正则自同构,则 包含在
包含在 中。
中。
定理1.1的证明 (i) 取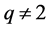 ,根据引理2.2的(ii)我们可以知道对于任意的正整数
,根据引理2.2的(ii)我们可以知道对于任意的正整数 ,
, 诱导了
诱导了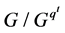 的正则自同构
的正则自同构 。易知
。易知 的阶数整除4。由命题1.1和引理2.3知道
的阶数整除4。由命题1.1和引理2.3知道 包含在
包含在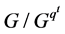 的中心里。因此
的中心里。因此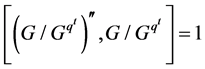 。即
。即 。从而
。从而
 。
。
进而
 。
。
因为 ,所以
,所以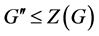 。
。
(ii) 记 ,只需证
,只需证 是Abel群即可。取
是Abel群即可。取 ,考虑
,考虑 。如果
。如果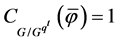 ,则
,则 是
是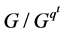 的2阶正则自同构。由命题1.1知道
的2阶正则自同构。由命题1.1知道 是Abel群。因此对于任意的
是Abel群。因此对于任意的 ,有
,有 。即
。即 。因为
。因为 ,所以
,所以 。这表明
。这表明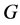 是Abel群。显然
是Abel群。显然 也是Abel群。如果
也是Abel群。如果 ,则
,则 是
是 -不变,因此
-不变,因此 是
是 的1阶或2阶自同构。注意到
的1阶或2阶自同构。注意到
 ,
,
于是 是
是 的正则自同构。因为
的正则自同构。因为 ,所以
,所以 是
是 的2阶正则自同构。由命题1.1知道
的2阶正则自同构。由命题1.1知道 是Abel群。注意到
是Abel群。注意到
 ,
,
我们有 是Abel群。所以对于任意的
是Abel群。所以对于任意的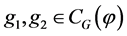 ,有
,有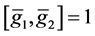 。即
。即 。因为
。因为 ,所以
,所以 。这表明
。这表明 是Abel群。
是Abel群。
基金项目
河北省教育厅青年基金(QN2016184),河北工程大学博士基金和河北工程大学研究生教育教学改革研究项目(161290140004)资助。
文章引用
马 晓迪,徐 涛. 有限生成无挠幂零群的4阶自同构
Finitely Generated Torsion-Free Nilpotent Groups Admitting an Automorphism of Order Four[J]. 理论数学, 2016, 06(05): 437-440. http://dx.doi.org/10.12677/PM.2016.65059
参考文献 (References)
- 1. Robinson, D.J.S. (1996) A Course in the Theory of Groups. 2nd Edition, Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4419-8594-1
- 2. Burnside, W. (1955) Theory of Groups of Finite Order. 2nd Edition, Dover Publications Inc., New York.
- 3. Gorenstein, D. (1980) Finite Groups. Chelsea Publishing Company, New York.
- 4. Neumann, B.H. (1956) Group with Automorphisms That Leave Only the Neutral Element Fixed. Archiv der Mathematik, 7, 1-5. http://dx.doi.org/10.1007/BF01900516
- 5. Thompson, J. (1959) Finite Groups with Fixed-Point-Free Automorphisms of Prime Order. Proc. Nat. Acad. Sci., 45: 578-581. http://dx.doi.org/10.1073/pnas.45.4.578
- 6. Higman, G. (1957) Groups and Rings Having Automorphisms without Non-Trivial Fixed Elements. Journal of the London Mathematical Society, 64, 321-334. http://dx.doi.org/10.1112/jlms/s1-32.3.321
- 7. 徐涛, 刘合国. 有限秩的可解群的正则自同构[J]. 数学年刊, 2014, 35A(5): 543-550.
- 8. Xu, T. and Liu, H.G. (2016) Finitely Generated Torsion-Free Nilpotent Groups Admitting an Automorphism of Prime Order. Communications in Mathematical Sciences, 32, 167-172.
- 9. Kovács, L.G. (1961) Group with Regular Automorphisms of Order Four. Mathematische Zeitschrift, 75, 277-294. http://dx.doi.org/10.1007/BF01211026
*通讯作者。