Pure Mathematics
Vol.06 No.06(2016), Article ID:19111,31
pages
10.12677/PM.2016.66068
Research on the Implementation of the Optimal Implementation of the Multi-Asset Option
Xiaoqing Wu
College of Science, Southwest Petroleum University, Chengdu Sichuan

Received: Nov. 10th, 2016; accepted: Nov. 24th, 2016; published: Nov. 30th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we study the problem of determining the optimal implementation boundary of multi- asset option, and establish a mathematical model of multidimensional Black-Scholes equation with singular inner boundary function vector 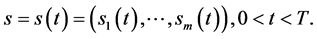 In multi-dimension region
In multi-dimension region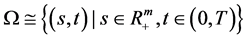 , the option price function is an unknown function. The exact solution
, the option price function is an unknown function. The exact solution  of the mathematical model is obtained by using the matrix theory and the generalized characteristic function method. And the exponential function vector expression of the singular inner boundary is obtained
of the mathematical model is obtained by using the matrix theory and the generalized characteristic function method. And the exponential function vector expression of the singular inner boundary is obtained . It is demonstrated that: when any
. It is demonstrated that: when any , the maximum value
, the maximum value 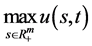 of the solution
of the solution  of the region
of the region is obtained on the singular boundary, namely
is obtained on the singular boundary, namely . The free boundary problem A and free boundary problem B of Black-Scholes equation are solved. The free boundary of problem A and B is expressed by the function vector
. The free boundary problem A and free boundary problem B of Black-Scholes equation are solved. The free boundary of problem A and B is expressed by the function vector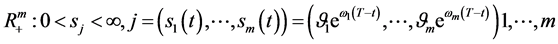 . The free boundary of the problem A and problem B coincides with the singular inner boundary. So the vector expression of the exponential function is the best implementation of the boundary. The exponential function vector
. The free boundary of the problem A and problem B coincides with the singular inner boundary. So the vector expression of the exponential function is the best implementation of the boundary. The exponential function vector satisfies the condition
satisfies the condition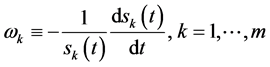 ; and
; and 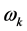 is calculated by
is calculated by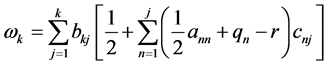 ; the formula shows that
; the formula shows that 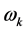 is only determined by all the parameters appearing in the multidimensional Black-Scholes equation.
is only determined by all the parameters appearing in the multidimensional Black-Scholes equation.
Keywords:Multi-Asset Option, Best Implementation Boundary, Free Boundary Problem, Multi-Dimension Black-Scholes Equation

多资产期权确定最佳实施边界问题的研究
吴小庆
西南石油大学理学院,四川 成都

收稿日期:2016年11月10日;录用日期:2016年11月24日;发布日期:2016年11月30日

摘 要
本文研究多资产期权确定最佳实施边界的问题,建立了多维Black-Scholes方程在多维区域 具有奇异内边界函数向量
具有奇异内边界函数向量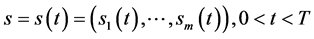 的数学模型,期权价格函数为未知函数。应用矩阵理论和广义特征函数法获得了期权价格函数的精确解
的数学模型,期权价格函数为未知函数。应用矩阵理论和广义特征函数法获得了期权价格函数的精确解 。并获得了奇异内边界的指数函数向量表达式
。并获得了奇异内边界的指数函数向量表达式 。证眀了:当任意
。证眀了:当任意 ,数学模型的解
,数学模型的解 在奇异内边界取区域
在奇异内边界取区域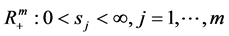 中的最大值,即
中的最大值,即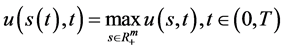 ;同时获得了 Black-Scholes方程的自由边界问题A和自由边界问题B的精确解和其自由边界的指数函数向量表达式
;同时获得了 Black-Scholes方程的自由边界问题A和自由边界问题B的精确解和其自由边界的指数函数向量表达式 ,问题A和问题B的自由边界与奇异内边界重合。从而指数函数向量表达式
,问题A和问题B的自由边界与奇异内边界重合。从而指数函数向量表达式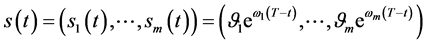 为最佳实施边界。指数函数向量
为最佳实施边界。指数函数向量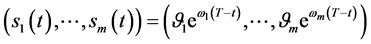 满足条件
满足条件 ;且有
;且有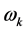 的计算公式
的计算公式 ;公式表明
;公式表明 由多维Black-Scholes方程中出现的所有参数
由多维Black-Scholes方程中出现的所有参数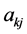 ,
,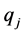 ,
,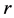 唯一确定。
唯一确定。
关键词 :多资产期权,最佳实施边界,自由边界问题,多维Black-Scholes方程

1. 引言
期权是风险管理的核心工具,姜礼尚 [1] 对期权定价理论作了系统深入的阐述,利用偏微分方程理论和方法对期权理论作深入的定性和定量分析,特别对美式期权展开了深入的讨论。美式期权合约中具有提前实施的条款,因此最佳实施边界的确定对于美式期权具有特殊意义。在美式期权定价研究中,姜礼尚 [1] 建立了Black-Scholes方程的自由边界问题,对最佳实施边界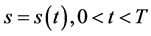 作了很多深入的研究,得到很多重要的结论。其中包括
作了很多深入的研究,得到很多重要的结论。其中包括 的位置,
的位置, 的单调性,
的单调性, 的上下界以及
的上下界以及 的凸性等,并给出了
的凸性等,并给出了 在
在 附近的渐近表达式。这些结果增加了对最佳实施边界的认识,对美式期权定价的数值计祘产生了重要的影响。期权定价问题历来是金融经济学中的重要研究课题之一 [1] - [8] ,多年来,众多经济学者与研究人员对这一问题进行不断深入的研究,但是这些研究大多是围绕具有单个资产的期权进行的。多资产期权在现代金融交易市场中占有重要的地位,研究多资产(或单个资产)期权定价模型大多是围绕数值解法进行的 [9] - [21] ,姜礼尚 [1] 建立了关于期权价格函数
附近的渐近表达式。这些结果增加了对最佳实施边界的认识,对美式期权定价的数值计祘产生了重要的影响。期权定价问题历来是金融经济学中的重要研究课题之一 [1] - [8] ,多年来,众多经济学者与研究人员对这一问题进行不断深入的研究,但是这些研究大多是围绕具有单个资产的期权进行的。多资产期权在现代金融交易市场中占有重要的地位,研究多资产(或单个资产)期权定价模型大多是围绕数值解法进行的 [9] - [21] ,姜礼尚 [1] 建立了关于期权价格函数 的多维Black-Scholes方程
的多维Black-Scholes方程
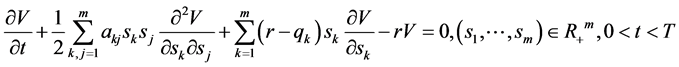 (01)
(01)
其中矩阵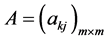 为实对称非负矩阵。研究关于方程(01)的多资产期权的数学模型。
为实对称非负矩阵。研究关于方程(01)的多资产期权的数学模型。
由于
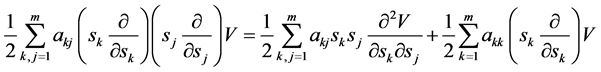 (02)
(02)
故方程(01)可改记为
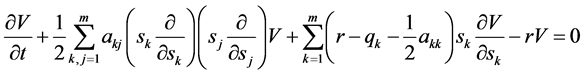 (03)
(03)
本文研究多资产期权确定最佳实施边界的问题,建立了多维Black-Scholes方程在多维区域 具有奇异内边界函数向量
具有奇异内边界函数向量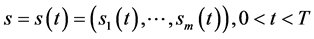 的数学模型,期权价格函数
的数学模型,期权价格函数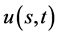 为未知函数。应用矩阵理论和广义特征函数法获得了数学模型的精确解
为未知函数。应用矩阵理论和广义特征函数法获得了数学模型的精确解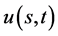 。并获得了奇异内边界的指数函数向量表达式
。并获得了奇异内边界的指数函数向量表达式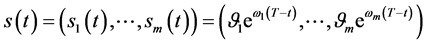 。证眀了:当任意
。证眀了:当任意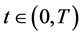 ,数学模型的解
,数学模型的解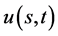 在奇异内边界取
在奇异内边界取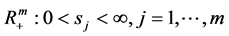 中的最大值,即
中的最大值,即 ;同时获得了Black-Scholes方程的自由边界问题A和自由边界问题B的精确解和其自由边界的指数函数向量表达式
;同时获得了Black-Scholes方程的自由边界问题A和自由边界问题B的精确解和其自由边界的指数函数向量表达式 ,问题A和问题B的自由边界与奇异内边界重合。从而指数函数向量表达式
,问题A和问题B的自由边界与奇异内边界重合。从而指数函数向量表达式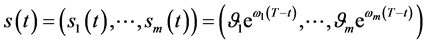 为最佳实施边界。指数函数向量
为最佳实施边界。指数函数向量 ,满足条件
,满足条件 ;且有
;且有 的计算公式
的计算公式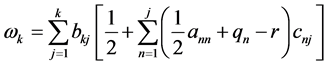 ;公式表明
;公式表明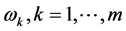 由多维Black-Scholes方程中出现的所有参数
由多维Black-Scholes方程中出现的所有参数 ,
, ,
,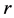 唯一确定。
唯一确定。
2. 主要结果
2.1. 多资产期权的数学模型I的研究
引入记号
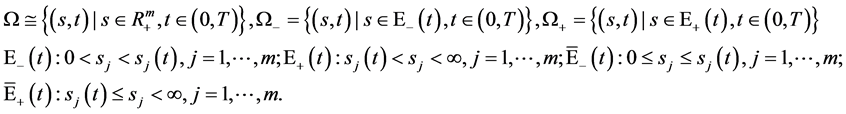
数学模型I (多维Black-Scholes方程具有奇异内边界的终值问题):
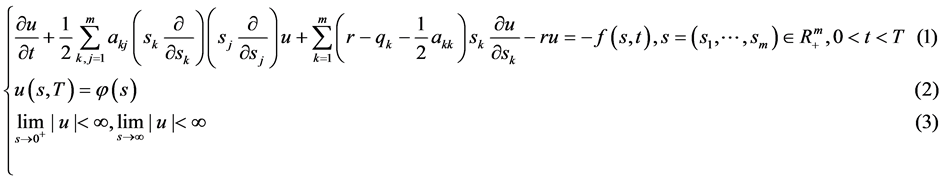
数学模型I是关于多资产期权的数学模型,它是多维Black-Scholes方程在区域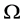 具有奇异内边界
具有奇异内边界 ,
,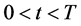 的终值问题,未知函数
的终值问题,未知函数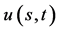 为期权价格函数。
为期权价格函数。
其中:方程的自由项为
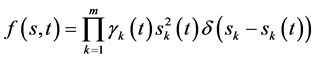 (4)
(4)
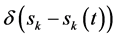 为狄拉克
为狄拉克 -函数;
-函数; 为
为 维狄拉克
维狄拉克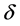 -函数;
-函数; ,
, 为实对称非负矩阵。
为实对称非负矩阵。
数学模型I.1 (多维Black-Scholes方程的终值问题):
 (5)
(5)
数学模型I.2 (多维Black-Scholes方程具有奇异内边界和齐次终值条件的终值问题):
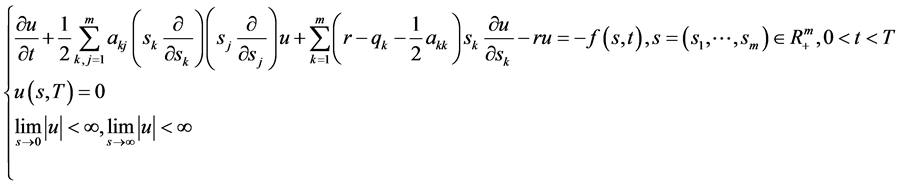 (6)
(6)
2.1.1. Black-Scholes方程数学模型I的求解
记偏微分算子
 (7)
(7)
先考虑m维Euler方程在半无界区域 的特征值问题I
的特征值问题I
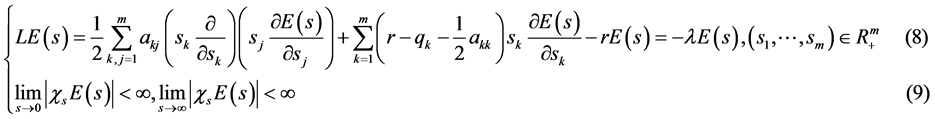
为求解特征值问题I我们建立了引理1.1~引理1.6。
引理1.1:设 为正定矩阵,则存在正线下三角矩阵
为正定矩阵,则存在正线下三角矩阵 满足
满足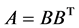 且分解是唯一的;且有
且分解是唯一的;且有
1) 正线下三角矩阵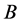 的行列式
的行列式 ,
,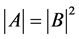 ;
;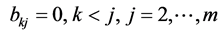 ;
;
2) 由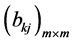 唯一确定
唯一确定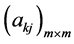 ;由
;由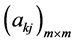 唯一确定
唯一确定 ;
;
3) 记 ,则
,则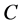 为正线上三角矩阵,
为正线上三角矩阵,
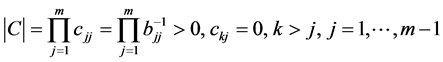 ;由
;由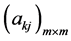 唯一确定
唯一确定 ;
;
4) 记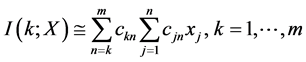 ,
,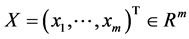 ;则当
;则当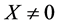 时,有
时,有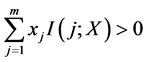 。从而当
。从而当 ,
, ,有
,有 ;
;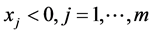 ,有
,有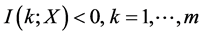 。
。
证明:由矩阵理论 [22] 即知存在正线下三角矩阵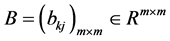 满足
满足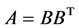 且分解是唯一的。由
且分解是唯一的。由 有
有 。
。
正线下三角矩阵 ,正线下三角矩阵
,正线下三角矩阵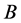 的行列式
的行列式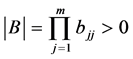 ,且
,且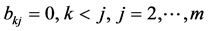 ;
; 的转置矩阵
的转置矩阵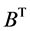 为正线上三角矩阵。
为正线上三角矩阵。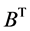 的逆矩阵
的逆矩阵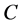 为正线上三角矩阵。
为正线上三角矩阵。 。
。
下证4)由于 为正线上三角矩阵,即有
为正线上三角矩阵,即有 和
和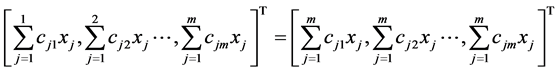 ;从而有
;从而有
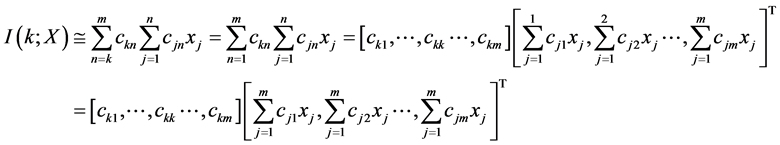
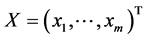 为列向量,应用分块矩阵的乘法运算即有
为列向量,应用分块矩阵的乘法运算即有
从而有
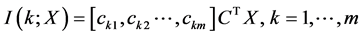 (10)
(10)
由于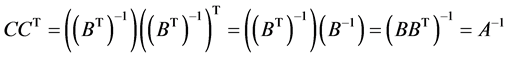 即有
即有
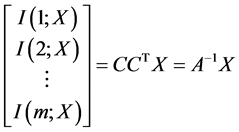 (11)
(11)
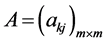 为正定矩阵,则
为正定矩阵,则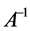 为正定矩阵,
为正定矩阵,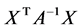 为正定二次齐式,从而有
为正定二次齐式,从而有
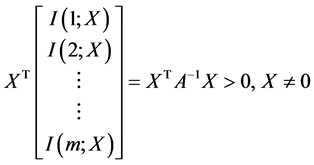 (12)
(12)
 (13)
(13)
由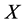 的任意性,分别令
的任意性,分别令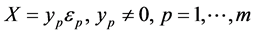 ,
,
其中 。
。
由(13)式即有
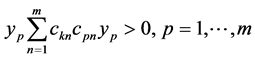
即
从而
 (14)
(14)
再记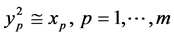 ;有
;有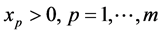 和
和
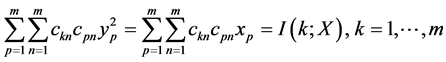 (15)
(15)
由(14),(15)两式即有:当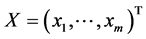 ,
,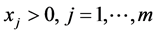 ,有
,有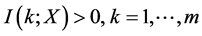 ;显然也有:当
;显然也有:当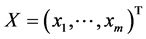 ,
, ,有
,有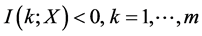 。引理证毕。
。引理证毕。
记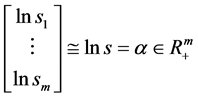 ,作
,作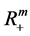 到
到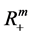 的线性变换
的线性变换
 (16)
(16)
记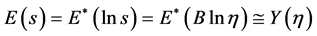 (17)
(17)
引理1.2:若 ,则有
,则有
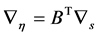 (18)
(18)
其中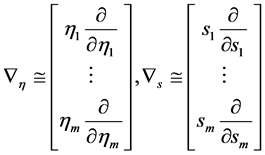 为向量变系数偏微分算子。
为向量变系数偏微分算子。
证明(16)式即
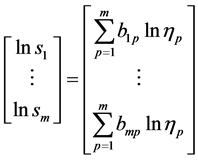 (19)
(19)
由(17)式即有
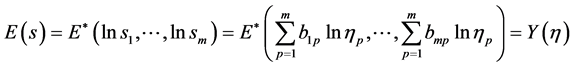 (20)
(20)
由复合函数的求导法则
 (21)
(21)
从而
即(18)式成立。引理证毕。
m维Euler方程在半无界区域 的特征值问题II
的特征值问题II

其中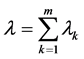 ,
, (24)
(24)
引理1.3:若 ,则特征值问题I中方程(8)与特征值问题II中方程(22)等价。
,则特征值问题I中方程(8)与特征值问题II中方程(22)等价。
证明:由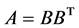 ,有
,有
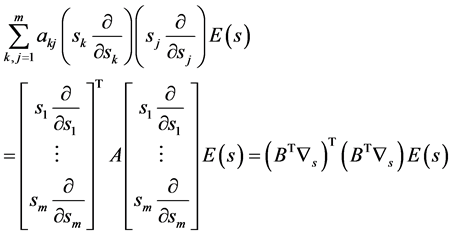 (25)
(25)
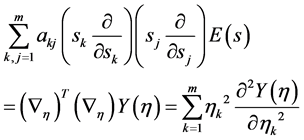 (26)
(26)
记 ,由引理1.1矩阵
,由引理1.1矩阵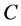 为正线上三角矩阵。
为正线上三角矩阵。
由(18)式有
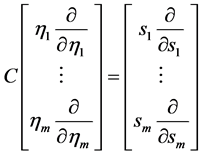 (27)
(27)
由矩阵乘法
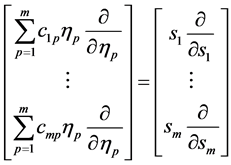 (28)
(28)
从而
 (29)
(29)
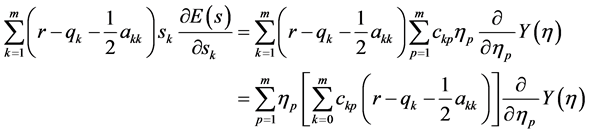 (30)
(30)
由于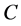 为正线上三角矩阵有
为正线上三角矩阵有

记
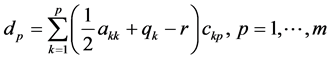 (31)
(31)
即有
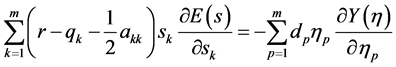 (32)
(32)
由(26),(32)两式即知方程(8)与方程(22)等价。引理证毕。
引理1.4:特征值问题II的特征值
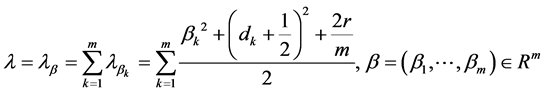 (33)
(33)
所对应的特征函数为
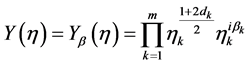 (34)
(34)
且有
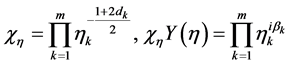 (35)
(35)
证明:容易求解特征值问题II:由分离变量法令
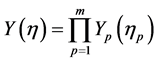 (36)
(36)
 (37)
(37)
再令
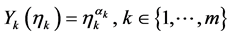 (38)
(38)

 (39)
(39)
 (40)
(40)
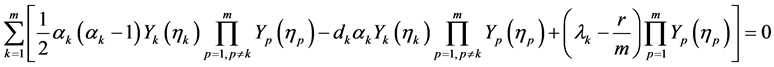
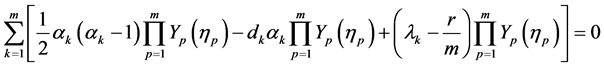 (41)
(41)
 (42)
(42)
若(42)式成立则(41)式成立;特征函数
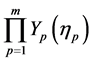
不恒为零,由(42)推出
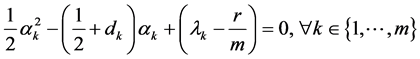 (43)
(43)
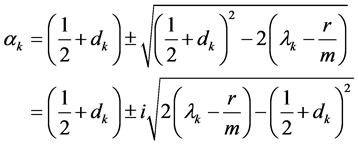
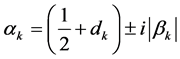
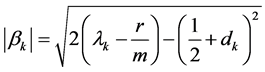
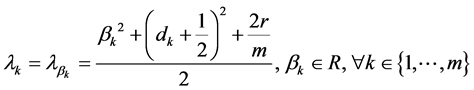 (44)
(44)
 (45)
(45)
 (46)
(46)
 (47)
(47)
 (48)
(48)
由(48)式即有(23)式成立。引理证毕。
由(16)和(17)式换回原变量即得特征值问题I的特征函数
 (49)
(49)
且
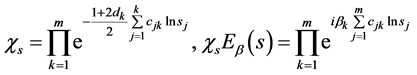 (50)
(50)
 (51)
(51)
由(51)式即有(9)式成立。于是得到
引理1.5:特征值问题I的特征值
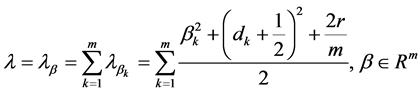 (52)
(52)
所对应的特征函数为
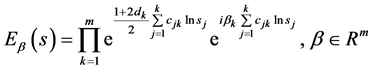 (53)
(53)
引理1.6:特征值问题I的特征函数系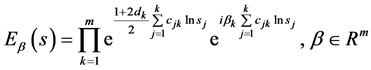 是半无界区域
是半无界区域 带权函数
带权函数 的完备正交系;正交关系即
的完备正交系;正交关系即
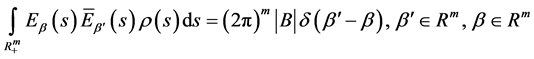 (54)
(54)
证明:由于
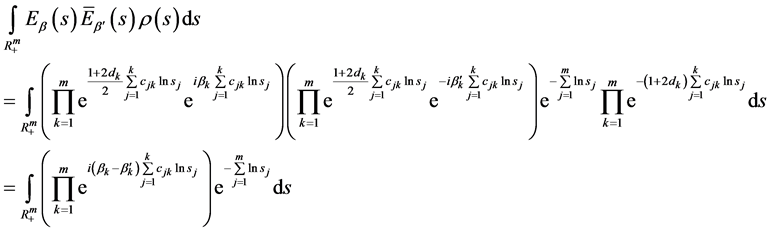 (55)
(55)
引入变量代换
 (56)
(56)
由于行列式
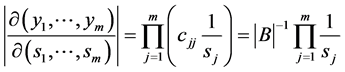
即有变量替换的雅可比行列式
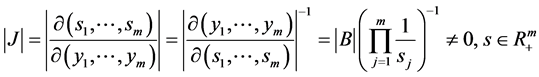 (57)
(57)
由多重积分变量替换公式,即有

 (58)
(58)
(58)式即(54)式。引理证毕。
由引理1.5与引理1.6的结论可以引入广义特征函数法 [23] [24] 求解 数学模型I。
不妨设解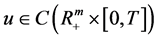 ,将其表为特征函数的积分形式
,将其表为特征函数的积分形式
 (59)
(59)
将上式两边乘以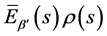 再关于变量
再关于变量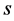 在
在 积分,利用正交关系(54)则有
积分,利用正交关系(54)则有
 (60)
(60)
得到
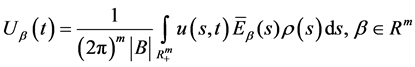 (61)
(61)
将方程中的自由项 也表为特征函数的积分形式
也表为特征函数的积分形式
 (62)
(62)
由(61)即有
 (63)
(63)
应用 -函数的积分性质即得
-函数的积分性质即得
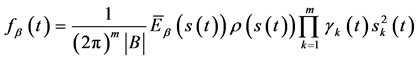 (64)
(64)
含参变量积分与算子 的运算交换次序即有
的运算交换次序即有
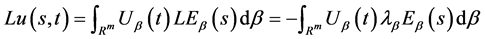 (65)
(65)
 (66)
(66)
由(2)即有
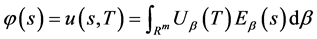 (67)
(67)
 (68)
(68)
将(62),(65),(66)代入方程(1)即有
 (69)
(69)
由特征函数系的完备正交性即有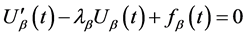 ,再由(68)式即得
,再由(68)式即得
非齐次常微分方程的终值问题
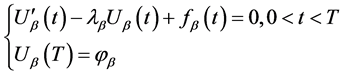 (70)
(70)
用常数变易法得到非齐次常微分方程的终值问题的解为
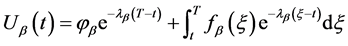 (71)
(71)
将上式代入(59)式即得
 (72)
(72)
将 的表达式(52),(53)代入(72),并记
的表达式(52),(53)代入(72),并记
 (73)
(73)
 (74)
(74)
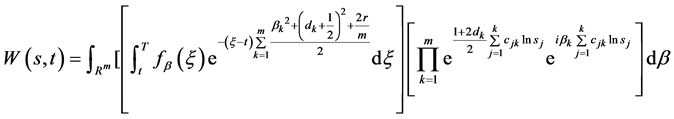 (75)
(75)
其中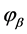 由(68),
由(68),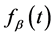 由(64)确定。
由(64)确定。
由(74)式即有
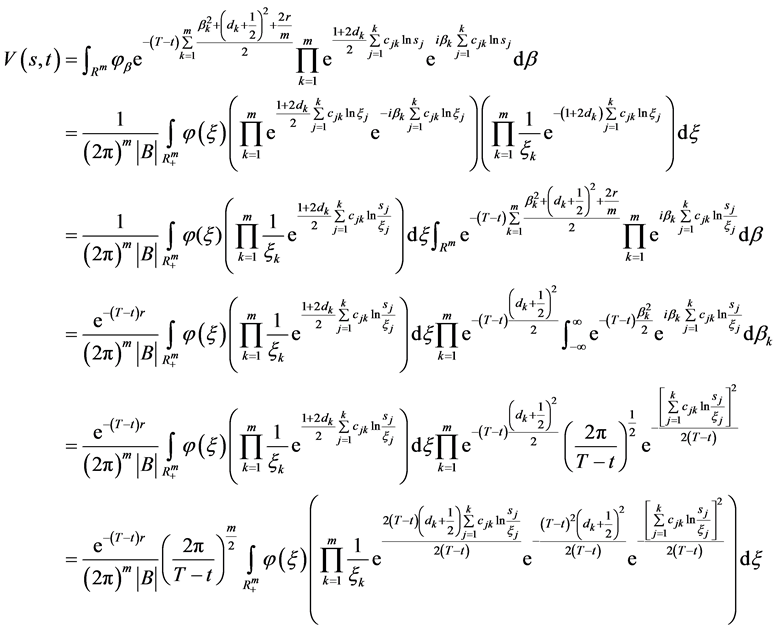

于是有
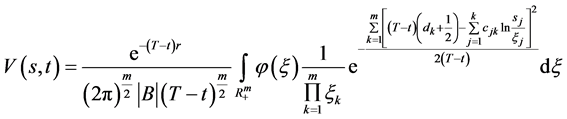 (76)
(76)
将 的表达式代入(64)式,化简即得
的表达式代入(64)式,化简即得
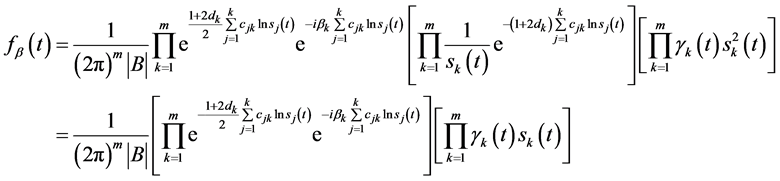 (77)
(77)
将(77)代入(75)式,并化简
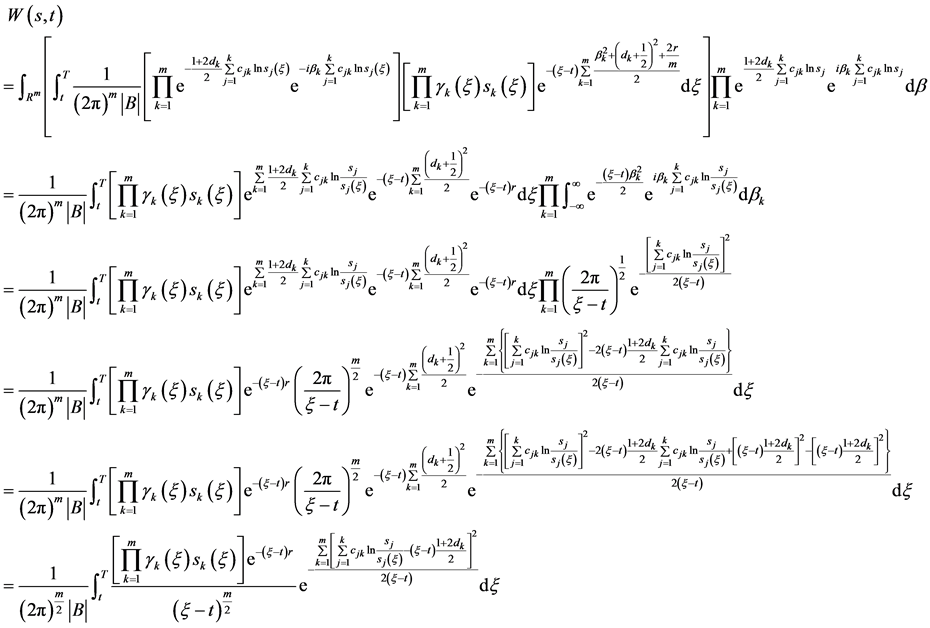
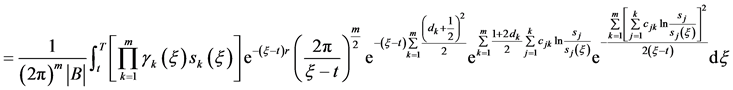
即得
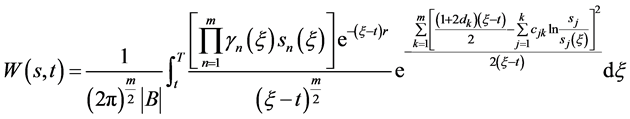 (78)
(78)
定理1 (数学模型I解的存在定理):若
1) 为正定对称矩阵,
为正定对称矩阵,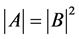 ;
;
2)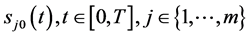 为充分光滑的单调函数;
为充分光滑的单调函数;
3) 。
。
则数学模型I有精确解:
 (79)
(79)
 (80)
(80)
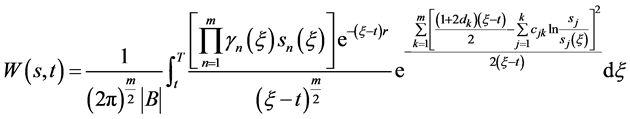 (81)
(81)
且数学模型I.1的解 由(80)式给出,数学模型I.2的解
由(80)式给出,数学模型I.2的解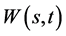 由(81)式给出。
由(81)式给出。
2.1.2. 多维Black-Scholes方程奇异内边界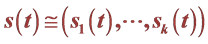 的确定
的确定
数学模型II (多维Black-Scholes方程确定奇异内边界的终值问题):
求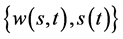 ,使其满足
,使其满足

定理2 (数学模型II解的存在定理):若
1) 为正定对称矩阵;
为正定对称矩阵;
2)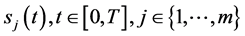 为充分光滑的单调函数;
为充分光滑的单调函数;
3)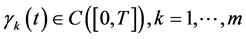 。
。
则数学模型II有连续有界的精确解

数学模型II有解的相容性条件是
 (89)
(89)
其中
 (90)
(90)
 (91)
(91)
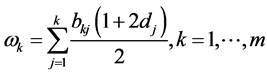 (92)
(92)
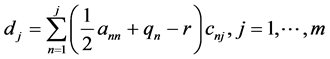 (93)
(93)
证明:由定理1(数学模型I解的存在定理)的结论,(81)式给出的 已满足条件(82) (83) (85)三式,让
已满足条件(82) (83) (85)三式,让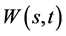 满足条件(84)式去确定奇异内边界
满足条件(84)式去确定奇异内边界 。
。
将(81)式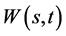 记为
记为
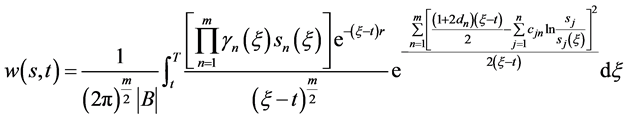 (94)
(94)
由(94)式对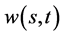 关于自变量
关于自变量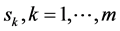 求偏导,由复合函数的求导法则有
求偏导,由复合函数的求导法则有
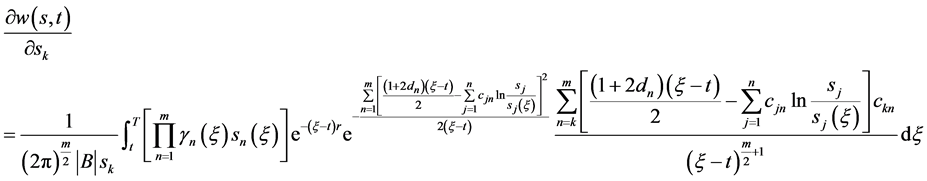 (95)
(95)
若令
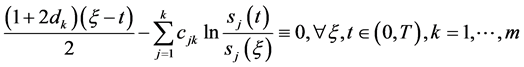 (96)
(96)
则

即有
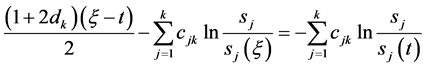 (97)
(97)
将(97)式代入(95)式即有
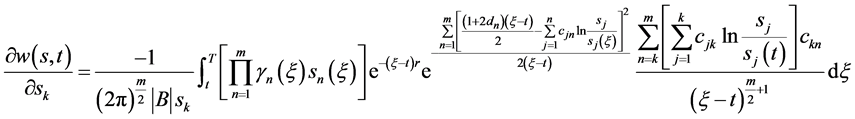 (98)
(98)
下面建立引理2.1~引理2.4来完成定理2的证明。
引理2.1:条件(96)成立,则有
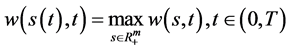 (99)
(99)
和
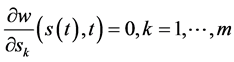 (100)
(100)
证明:若条件(96)成立,则有(98)成立。由(98)式易知(100)式成立。
由(98)即得到対任意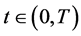 有
有
1) 当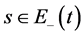 有
有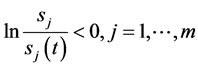
由引理1.1的结论4)即有即有:当 ,有
,有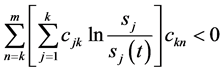 成立,从而
成立,从而
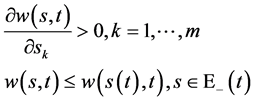 (101)
(101)
2) 当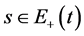 有
有
由引理1.1中结论4)即有:当 ,有
,有 成立,从而
成立,从而
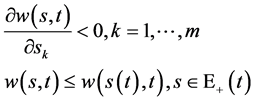 (102)
(102)
从而(99)式成立。引理证毕。
引理2.2:条件
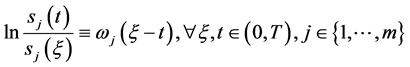 (103)
(103)
成立的充要条件为
 (104)
(104)
证明:1) 必要性,若(103)成立,由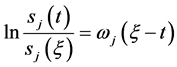 即有
即有
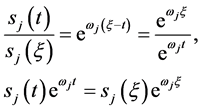 (105)
(105)
记
 (106)
(106)
由(105)式有
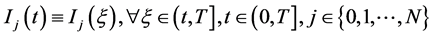 (107)
(107)
让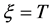 即有
即有
 (108)
(108)
干是有(104)式成立。
2) 充分性,若(104)式成立,即有

即(103)成立。引理证毕。
引理2.3:当条件
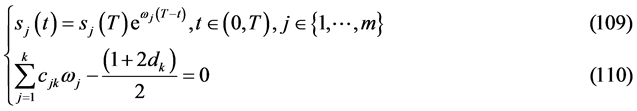
成立时,则条件(96)成立,从而有 。
。
证明:由(109)式则有
 (111)
(111)
再由(110)式即有
 (112)
(112)
即条件(96)成立,由引理2.1即有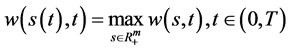 成立。引理证毕。
成立。引理证毕。
引理2.4:未知数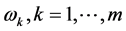 的线性方程组(110)的解为
的线性方程组(110)的解为
 (113)
(113)
证明:线性方程组(110)写成矩阵形式即为
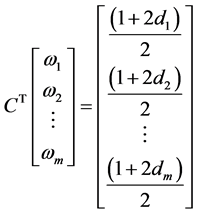 (114)
(114)
由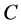 矩阵的定义即有
矩阵的定义即有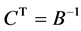 ,从而
,从而
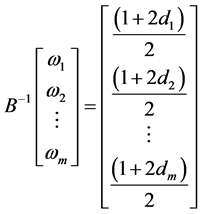 (115)
(115)
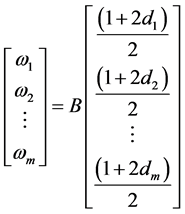 (116)
(116)
由矩阵乘法即得线性方程组(110)的解由(113)式给出。引理证毕。
记
 (117)
(117)
由引理2.1~引理2.4即知:当(117)成立时,有解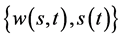 其中
其中 由(94)给出,
由(94)给出,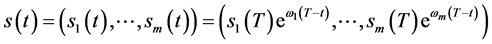 。由(117)式即有(96)成立,由引理2.1即有
。由(117)式即有(96)成立,由引理2.1即有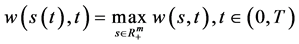 和
和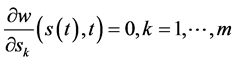 成立。
成立。
由(117)式即有(97)式成立,将(97)代入(94)即有:
 (118)
(118)
再将(117)式代入(118)式,即有
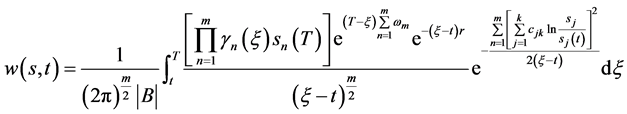 (119)
(119)
引入记号: ,再由(119)即得到
,再由(119)即得到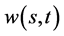 由(87)给出。由(87)式给出的解
由(87)给出。由(87)式给出的解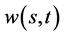 满足条件(84)式和(85)式。从而满足数学模型II,即(87),(88)两式给出了数学模型II的解。由(87)式即知数学模型II有解的相容性条件是(89)式。定理证毕。
满足条件(84)式和(85)式。从而满足数学模型II,即(87),(88)两式给出了数学模型II的解。由(87)式即知数学模型II有解的相容性条件是(89)式。定理证毕。
引入记号

多维开区间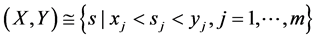 ,多维闭区间
,多维闭区间 。
。
函数的支集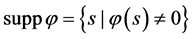 ,支集的闭包
,支集的闭包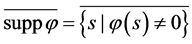 ,记函数集合
,记函数集合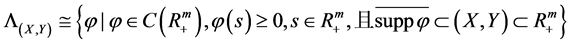 。
。
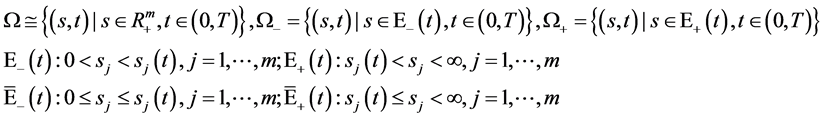
记
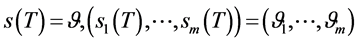 (120)
(120)
 (121)
(121)
定理3(数学模型I.1解的性质定理):若 为正定矩阵,
为正定矩阵, ;则
;则
1) 当 ;数学模型I.1的解
;数学模型I.1的解
 (122)
(122)
满足
 (123)
(123)
和
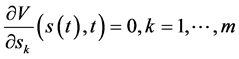 (124)
(124)
其中
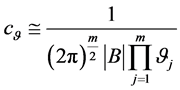 (125)
(125)
2) 当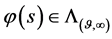 ,则数学模型I.1的解
,则数学模型I.1的解
 (126)
(126)
且解 满足
满足
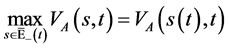 (127)
(127)
3) 当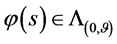 ,数学模型I.1的解
,数学模型I.1的解
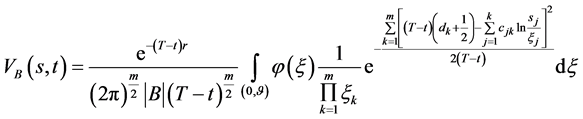 (128)
(128)
且解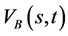 满足
满足
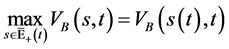 (129)
(129)
证1): 数学模型I.1的解由定理1的(74)式给出,由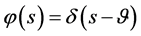 有
有
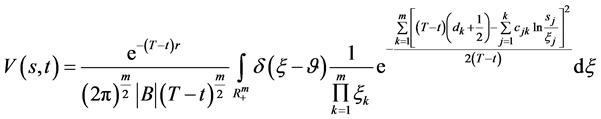 (130)
(130)
应用多维狄拉克 -函数的积分性质即得
-函数的积分性质即得
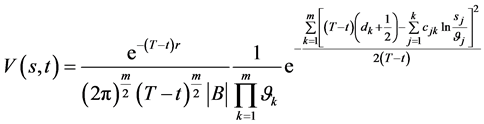 (131)
(131)
引入记号 即有
即有
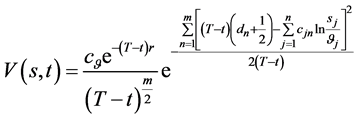 (132)
(132)
由于 线性方程组(110)的解,由(110)即有
线性方程组(110)的解,由(110)即有
 (133)
(133)
由(112)式即有
即有
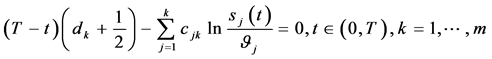 (134)
(134)
由(132)和(134)两式即有
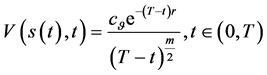 (135)
(135)
由于
 (136)
(136)
从而
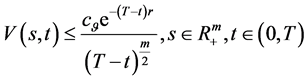 (137)
(137)
故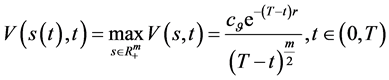 。由(132)对
。由(132)对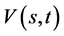 关于
关于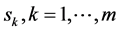 求偏导得到
求偏导得到
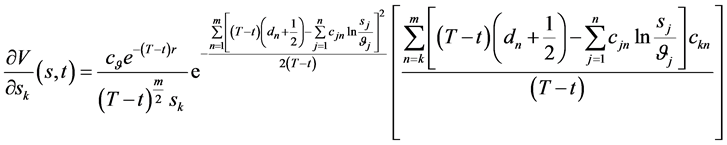 (138)
(138)
 (139)
(139)
由(134),(139)即得(124)。
证2):数学模型I.1的解由定理1的(74)式给出。任意 即有
即有 。
。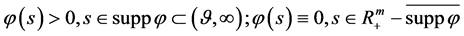 ,故
,故 ,
, 。于是(74)式中积分的积分区域由
。于是(74)式中积分的积分区域由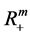 变为
变为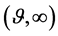 。则数学模型I.1的解
。则数学模型I.1的解
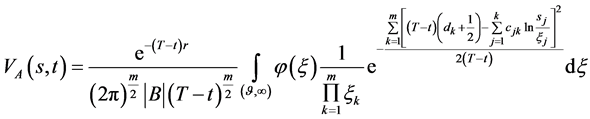 (140)
(140)
由(140)关于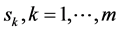 求偏导
求偏导
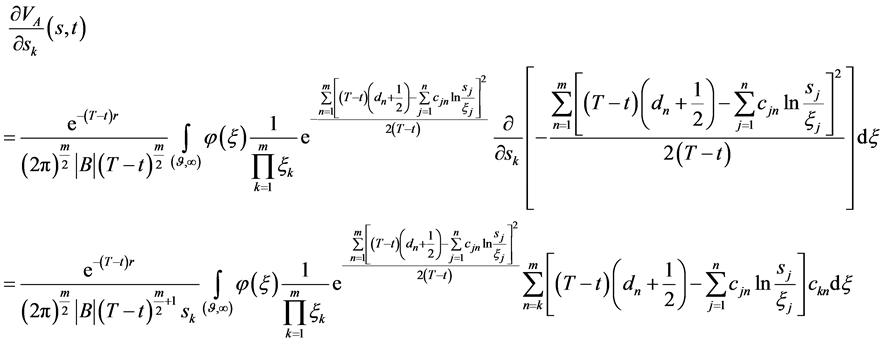
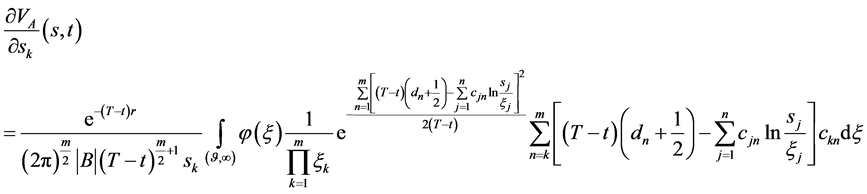 (141)
(141)
当 有
有 ;积分变量
;积分变量 ,有
,有 ;
;
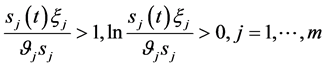 (142)
(142)
又
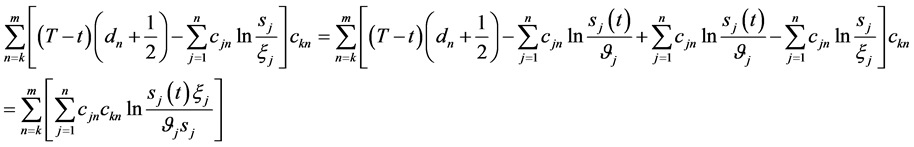 (143)
(143)
记
 ;由(142),有
;由(142),有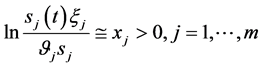 ,引理1.1的结论4)即有
,引理1.1的结论4)即有 ;
;
从而由(143)有
 (144)
(144)
再由(141)即有当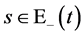 ,
,
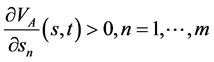 (145)
(145)
当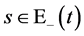 ,
, ,从而有
,从而有 成立。
成立。
证3):当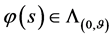 ,由数学模型I.1的解(74)式即有(128)成立。由(128) 式对
,由数学模型I.1的解(74)式即有(128)成立。由(128) 式对 关于
关于 求偏导即有
求偏导即有
 (146)
(146)
当 ,有
,有 ,
,
引理1.1的结论4)即有
由(146)即有:当 ,
,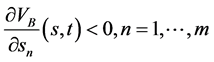 。当
。当 ,
,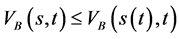 ,从而有
,从而有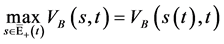 成立。定理证毕。
成立。定理证毕。
2.2. 关于多维Black-Scholes方程的自由边界问题的研究
由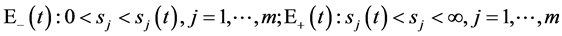
即有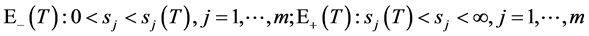
即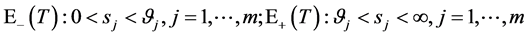
即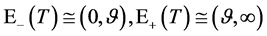
下面分别讨论关于多维Black-Scholes方程在 的自由边界问题A和在
的自由边界问题A和在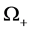 的自由边界问题B。
的自由边界问题B。
自由边界问题A (关于多维Black-Scholes方程在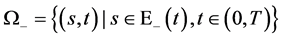 的自由边界问题):求
的自由边界问题):求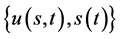 ,使其满足
,使其满足
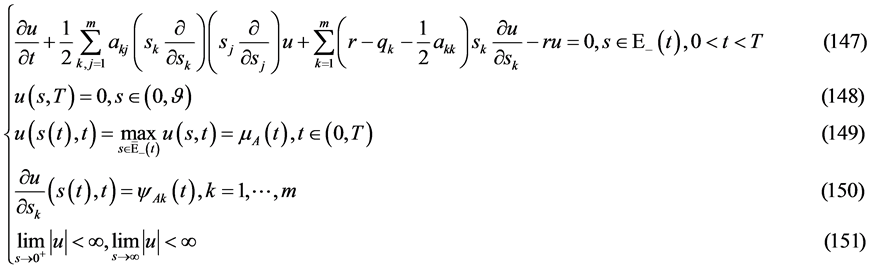
定理4 (自由边界问题A多解性定理):若
1)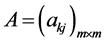 为正定矩阵;
为正定矩阵;
2) ;
;
则自由边界问题A的有解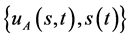 ,自由边界为
,自由边界为
 (152)
(152)
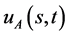 具有多解性,第一解:
具有多解性,第一解:
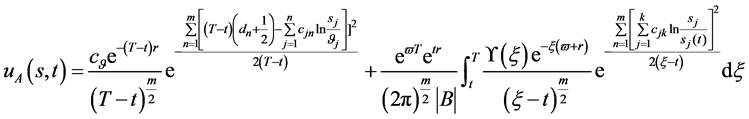 (153)
(153)
有解的相容性条件
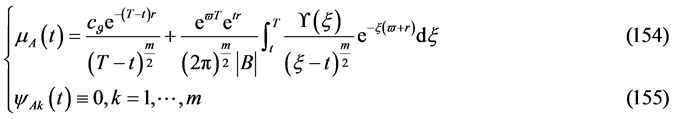
第二解:
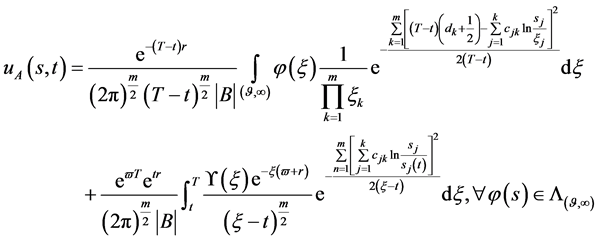 (156)
(156)
有解的相容性条件
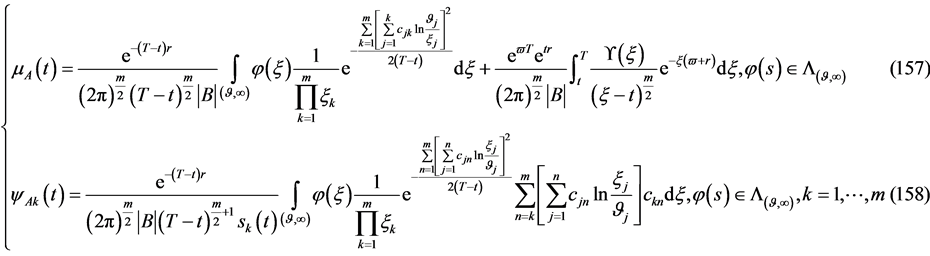
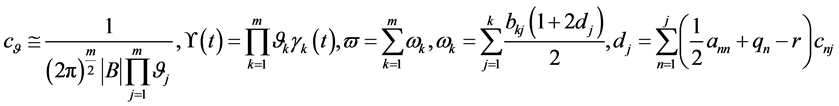 (159)
(159)
证明:当 由定理2的(87)式给出的解滿足齐次方程(147),故由(153)式和(156)式给出的解滿足齐次方程(147)。再由定理2,定理3的结论即知定理4成立。由(112),(152)两式即有
由定理2的(87)式给出的解滿足齐次方程(147),故由(153)式和(156)式给出的解滿足齐次方程(147)。再由定理2,定理3的结论即知定理4成立。由(112),(152)两式即有
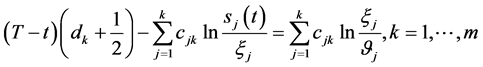 (160)
(160)
推证相容性条件(158),由(141),(160)两式即得。定理证毕。
附注1:定理4中的笫二解对在函数集合 任意给定的
任意给定的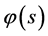 都有由(156)式给出的解
都有由(156)式给出的解 与之对应,即得到了一个解族
与之对应,即得到了一个解族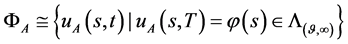 。
。
自由边界问题B (关于多维Black-Scholes方程在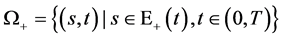 的自由边界问题):求
的自由边界问题):求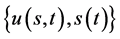 ,使其满足
,使其满足
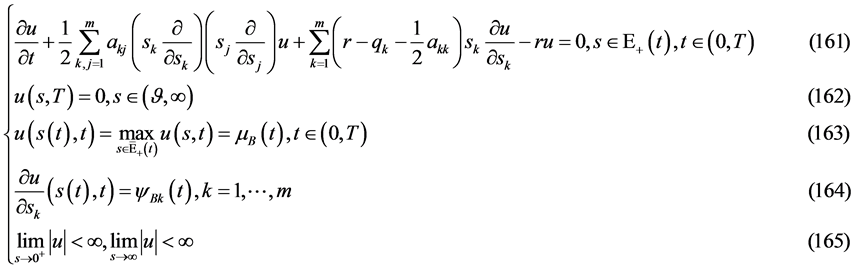
定理5 (自由边界问题B多解性定理):若
1) 为正定矩阵;
为正定矩阵;
2)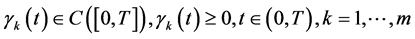 ;
;
则自由边界问题B有解 ,自由边界为
,自由边界为
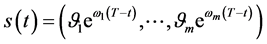 (166)
(166)
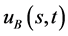 具有多解性,第一解:
具有多解性,第一解:
 (167)
(167)
有解的相容性条件
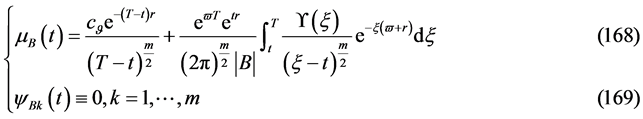
第二解:
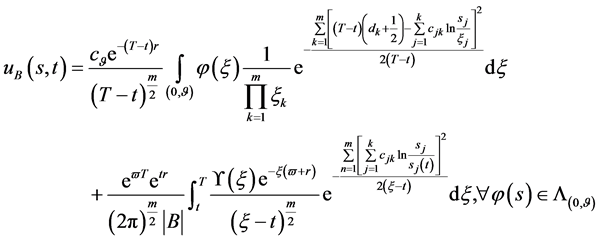 (170)
(170)
有解的相容性条件
 (171)
(171)
 (172)
(172)
其中
 (173)
(173)
证明:当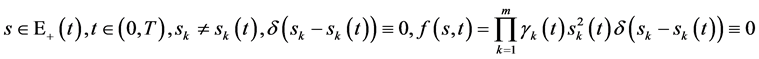 由定
由定
理2的(87)式给出的解滿足齐次方程(161),故由(167)式和(170)式给出的解滿足齐次方程(161)。再由定理2,定理3的结论即知定理5成立。推证相容性条件(172)由(146) (160)两式即得。定理证毕。
附注2:定理5中的笫二解对在函数集合 任意给定的
任意给定的 都有由(170)式给出的解
都有由(170)式给出的解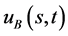 与之对应,即得到了一个解族
与之对应,即得到了一个解族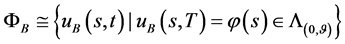 。
。
2.3. 数学模型III与自由边界问题A和问题B的关系
数学模型III (多维Black-Scholes方程确定奇异内边界的终值问题):
求 ,使其满足
,使其满足
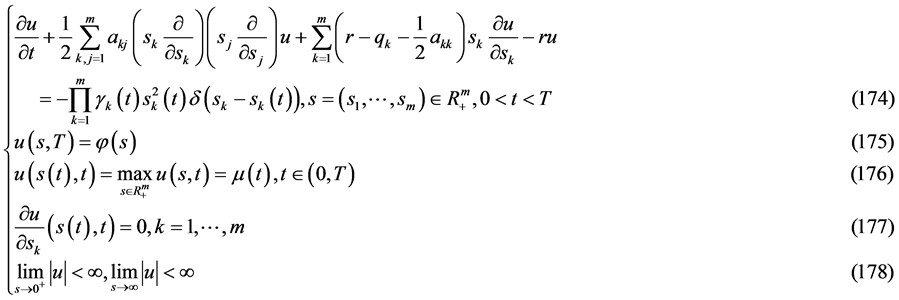
定理6 (奇异内边界与问题A和B的自由边界三线合一定理一):若
1)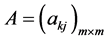 为正定矩阵;
为正定矩阵;
2)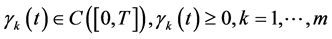 ;
;
3)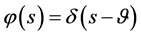 ;
;
4)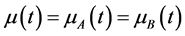 ;
;
5) 。
。
则数学模型III与问题A和问题B有相同表达式的解
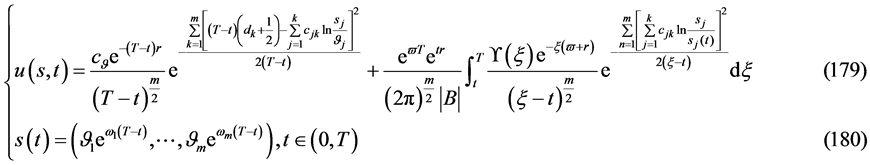
有解的相容性条件
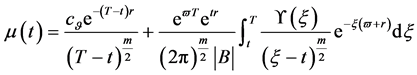 (181)
(181)
其中
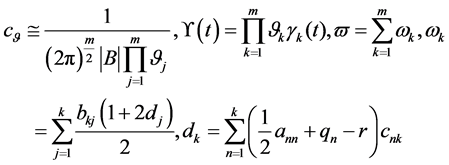 (182)
(182)
数学模型III的奇异内边界与问题A和问题B的自由边界三曲线重合成同一指数函数向量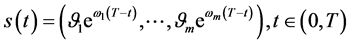 ;数学模型III的解函数是问题A和B的解函数的共同连续开拓,即
;数学模型III的解函数是问题A和B的解函数的共同连续开拓,即
 (183)
(183)
定义2:若 ,
,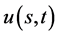 由(183)定义,称
由(183)定义,称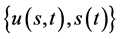 为数学模型III与问题A和问题B的一致相容解。
为数学模型III与问题A和问题B的一致相容解。
定理7 (奇异内边界与问题A和B的自由边界三线合一定理二):若
1)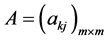 为正定矩阵;
为正定矩阵;
2)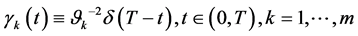 ;
;
3)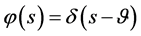 ;
;
4)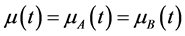 ;
;
5) 。
。
则数学模型III与问题A和问题B的一致相容解
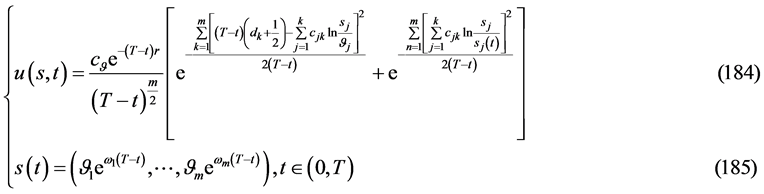
有解的相容性条件
 (186)
(186)
 (187)
(187)
定理8 (奇异内边界与问题A和问题B的自由边界三线合一定理三):若
1)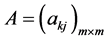 为正定矩阵;
为正定矩阵;
2) ;
;
3)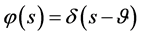 ;
;
4)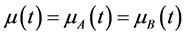 ;
;
5)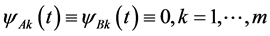 。
。
则数学模型III与问题A和问题B的一致相容解

有解的相容性条件
 (190)
(190)
其中
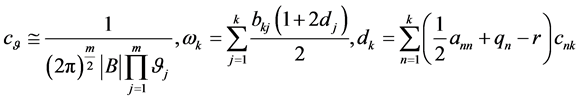 (191)
(191)
由定理6,定理7,定理8给出的一致相容解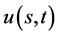 满足条件
满足条件
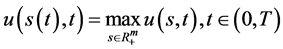 (192)
(192)
即一致相容解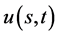 在任意时刻
在任意时刻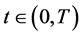 在
在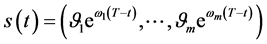 取
取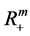 中的最大值
中的最大值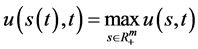 ,从而称
,从而称 为最佳实施边界。
为最佳实施边界。
定理9 (多资产期权最佳实施边界定理):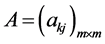 为正定矩阵,则期权价格函数
为正定矩阵,则期权价格函数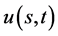 在任意时刻
在任意时刻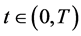 在
在
 取
取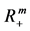 中的最大值
中的最大值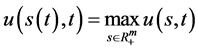 ,多资产期权最佳实施边界为指数函数向量
,多资产期权最佳实施边界为指数函数向量
 (193)
(193)
满足
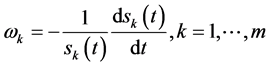 (194)
(194)
且有 的计算公式
的计算公式
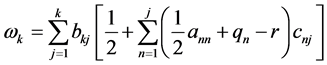 (195)
(195)
公式(195)表明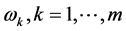 由多维Black-Scholes方程中出现的所有参数
由多维Black-Scholes方程中出现的所有参数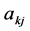 ,
,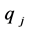 ,
,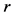 唯一确定。
唯一确定。
证明:由定理6,定理7,定理8即知期权价格函数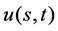 在任意时刻
在任意时刻 在
在
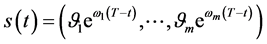 取
取 中的最大值
中的最大值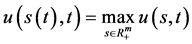 ,从而多资产期权最佳实施边界为指数函数向量(193)。关于
,从而多资产期权最佳实施边界为指数函数向量(193)。关于 的计算公式(93)式代入
的计算公式(93)式代入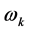 的计算公式(92)式即得
的计算公式(92)式即得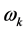 的计算公式(195),由引理1.1即知
的计算公式(195),由引理1.1即知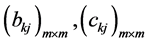 皆由
皆由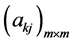 唯一确定,从而
唯一确定,从而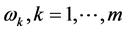 由多维Black-Scholes方程中出现的所有参数
由多维Black-Scholes方程中出现的所有参数 ,
, ,
, 唯一确定。定理证毕。
唯一确定。定理证毕。
3. 结论
指数函数向量 为多资产期权的最佳实施边界,满足条件
为多资产期权的最佳实施边界,满足条件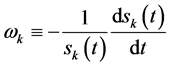 ;且
;且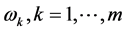 由多维Black-Scholes方程中出现的所有参数
由多维Black-Scholes方程中出现的所有参数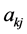 ,
,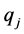 ,
,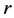 唯一确定。
唯一确定。
文章引用
吴小庆. 多资产期权确定最佳实施边界问题的研究
Research on the Implementation of the Optimal Implementation of the Multi-Asset Option[J]. 理论数学, 2016, 06(06): 496-526. http://dx.doi.org/10.12677/PM.2016.66068
参考文献 (References)
- 1. 姜礼尚. 期权定价的数学模型和方法[M]. 第2版. 北京: 高等教育出版社, 2008.
- 2. 姜礼尚, 徐承龙, 任学敏, 李少华. 金融数学丛书:金融衍生产品定价的数学模型与案例分析[M]. 第2版. 北京: 高等教育出版社, 2013.
- 3. 任学敏, 魏嵬, 姜礼尚, 梁进著. 信用风险估值的数学模型与案例分析[M]. 北京: 高等教育出版社, 2014.
- 4. 姜礼尚. 金融衍生产品定价的数学模型与案例分析[M]. 北京: 高等教育出版社, 2008.
- 5. 黄文礼, 李胜宏. 分数布朗运动驱动下带比例交易成本的期权定价[J]. 高校应用数学学报, 2011, 26(2): 201-208.
- 6. 冯骅. 金融产品及其衍生物价格的数学模型研究[D]: [硕士学位论文]. 北京: 中国石油大学(北京), 2011.
- 7. 袁世冉. 对一篮子期权定价模型的研究[D]: [硕士学位论文]. 秦皇岛: 燕山大学, 2014.
- 8. 胡宗义. 投资选择及资产定价数学模型研究[D]: [博士学位论文]. 长沙: 湖南大学, 2004.
- 9. 周杲昕. 多资产期权定价模型的数值新方法研究[D]: [硕士学位论文]. 北京: 华北电力大学, 2013.
- 10. 黎伟, 周圣武, Li Wei, Zhou Shengwu. 带交易费的多资产期权定价模型及数值解法[J]. 江苏师范大学学报(自然科学版), 2011, 29(2): 53-56.
- 11. 刘莉. 互换与极值期权定价的树网格法[D]: [硕士学位论文]. 桂林: 广西师范大学, 2008.
- 12. 许德志. 若干期权定价模型的数值新方法研究[D]: [硕士学位论文]. 北京: 华北电力大学(北京), 2010.
- 13. 张帆. 两类期权定价模型有限差分的并行计算[D]: [硕士学位论文]. 北京: 华北电力大学, 2014.
- 14. Broadie, M and Detemple, J. (1996) American Option Valuation: New Bounds, Approximations, and a Comparison of Existing Methods. Review of Financial Studies, 9, 1211-1250. https://doi.org/10.1093/rfs/9.4.1211
- 15. Figlewski, S. and Gao, B. (1999) The Adaptive Mesh Model: A New Approach to Efficient Option Pricing. Journal of Financial Economics, 53, 313-351. https://doi.org/10.1016/S0304-405X(99)00024-0
- 16. Figlewski, S. and Gao, B. (1998) The Adaptive Mesh Model: A New Approach to Efficient Option Pricing. New York University, Leonard N. Stern School of Business, New York.
- 17. Whaley, R.E. (1981) On the Valuation of American Call Options on Stocks with Known Dividends. Journal of Financial Economics, 9, 207-211. https://doi.org/10.1016/0304-405X(81)90013-1
- 18. Ankudinova, J. and Ehrhardt, M. (2008) On the Numerical Solution of Nonlinear Black-Scholes Equations. Computers & Mathematics with Applications, 56, 799-812. https://doi.org/10.1016/j.camwa.2008.02.005
- 19. Lötstedt, P., Persson, J. and Sydow, L.V. (2007) Space-Time Adaptive Finite Difference Method for European Multi-Asset Options. Computers & Mathematics with Applications, 53, 1159-1180. https://doi.org/10.1016/j.camwa.2006.09.014
- 20. Goodman, V. and Stampfli, J. (2001) The Mathematics of Finance: Modeling and Hedging. Pure and Applied Undergraduate Texts, 7, 250.
- 21. Broadie, M. and Detemple, J. (1995) American Capped Call Options on Dividend-Paying Assets. Review of Financial Studies, 8, 161-191. https://doi.org/10.1093/rfs/8.1.161
- 22. 史荣昌. 矩阵分析[M]. 北京: 北京理工大学出版社, 1996.
- 23. 吴小庆. 数学物理方程及其应用[M]. 北京: 科学出版社, 2008.
- 24. 吴小庆. 偏微分方程理论与实践[M]. 北京: 科学出版社, 2009.