Pure Mathematics
Vol.07 No.03(2017), Article ID:20533,8
pages
10.12677/PM.2017.73022
Analysis of Finite-Time Stability of Fractional-Order Chaotic System and Its Synchronization Control
Dandan Liu, Caixia Gao
Institute of Mathematical Science, Inner Mongolia University, Hohhot Inner Mongolia

Received: Apr. 29th, 2017; accepted: May 13th, 2017; published: May 17th, 2017

ABSTRACT
In this paper, the finite time stability and synchronization control of fractional order chaotic systems are studied; based on the Lyapunov fractional stability theory, the determination method of finite time stability for a class of nonlinear fractional chaotic systems is proposed, and it’s more generic than the existing results. And the synchronous controller is designed by the method; in the case of all the variables are met in the system, the different structure of the driver system and the response system are synchronized. Numerical simulation results demonstrate the effectiveness of the proposed method.
Keywords:Fractional-Order Chaotic System, Finite-Time Stability, Synchronization Control
分数阶混沌系统有限时间稳定性分析及 同步控制
刘丹丹,高彩霞
内蒙古大学数学科学学院, 内蒙古 呼和浩特
收稿日期:2017年4月29日;录用日期:2017年5月13日;发布日期:2017年5月17日

摘 要
本文研究了分数阶混沌系统有限时间稳定性及其同步控制,并基于Lyapunov分数阶稳定性理论提出了针对一类非线性分数阶混沌系统有限时间稳定的判定方法,与现有的结果相比其更具有一般性;并应用该方法设计了同步控制器,在满足系统所有变量有界的情况下实现了驱动系统和响应系统的异结构有限时间同步。数值仿真结果进一步验证了该方法的有效性。
关键词 :分数阶混沌系统,有限时间稳定,同步控制

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着分数阶微积分理论的不断成熟,分数阶混沌系统稳定性研究得到了国内外广大学者的关注。许多物理学过程都展现出分数阶动力行为,研究表明用分数阶建模可以更好的描述实际的物理现象 [1] [2] [3] [4] 。混沌同步由于在通信领域的广泛应用得到了很快的发展,人们相继提出了很多种整数阶混沌系统的同步方法,如滑模变结构控制法、自适应控制法、模糊控制法、脉冲控制法和Backstepping控制法等,并进一步推广到了分数阶混动系统 [5] - [13] 。但是,这些方法只是对系统稳定或渐近稳定进行了研究 [14] [15] [16] 。然而,在实际应用当中,更多的时候是要求闭环系统能够在有限时间内稳定,因此更需要关注系统的有限时间控制。另外,在设计有限时间稳定控制器时,都会存在复杂的分数幂项,这让闭环系统具有了更好的鲁棒性和抗干扰性。
针对分数阶混沌系统有限时间稳定,赵灵冬等利用分数阶微积分理论得到了一个分数阶混沌系统有限时间稳定的定理,并实现了分数阶超混沌Lorenz系统有限时间稳定 [17] 。赵建利等研究了洛伦兹–哈肯激光混沌系统有限时间稳定的主动控制方法,给出了整数阶混沌系统近似有限时间稳定的一个充分条件 [18] 。Jun Shen研究了非线性分数阶系统在有限时间内不存在稳定点的问题,推动了非线性系统有限时间稳定性理论的发展 [19] 。在非线性系统有限时间稳定理论中,陈国培等通过函数构造和变量替换给出了新的非线性系统有限时间稳定的充分条件 [20] ,具有很强的应用性,但是只是针对整数阶非线性系统,对于分数阶非线性系统有限时间稳定性理论的研究还尚未深入。
本文首先针对分数阶混沌系统,在原有的有限时间稳定理论的基础上,通过构造一个非负不减少连续函数,削弱了系统Lyapunov函数非负不增加的条件(允许在某些时间区间上出现单调增加的情况),其次利用新提出的方法设计了同步控制器,实现了驱动系统和响应系统的同步,最后通过仿真实验,验证了该方法和控制器的有效性。
2. 分数阶微积分
分数阶微积分概念提出了很多种定义,文中采用Caputo定义作为研究工具。
分数阶积分定义为
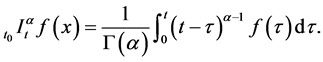 (1)
(1)
Caputo分数阶微分定义为
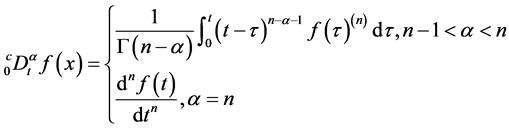 (2)
(2)
其中,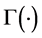 为Gamma函数。
为Gamma函数。
当 时,Caputo分数阶微分的解等价于
时,Caputo分数阶微分的解等价于
 (3)
(3)
定义1. 双参数Mittag-Leffler函数定义为
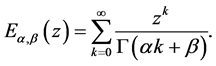 (4)
(4)
其中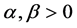 ,
,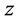 为复数,
为复数, 为Gamma函数,其Laplace变化定义为
为Gamma函数,其Laplace变化定义为

其中 为
为 的实部,
的实部,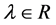 ,
,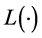 为Laplace变换。
为Laplace变换。
考虑如下非线性分数阶混沌系统:
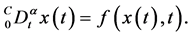 (5)
(5)
其中 ,
,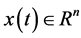 为系统状态,
为系统状态,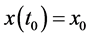 ,
,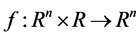 为满足局部Lipschitz条件的非线性函数。
为满足局部Lipschitz条件的非线性函数。
定义2. 对给定初始时刻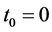 和正数
和正数 ,其中
,其中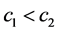 ,如果满足
,如果满足
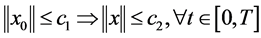
则称系统(5)关于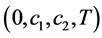 有限时间稳定。
有限时间稳定。
引理1. 如果有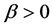 ,
,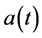 为定义在
为定义在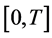 上的局部可积正定函数,
上的局部可积正定函数,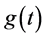 为定义在
为定义在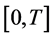 上的非负不减少连续函数,
上的非负不减少连续函数, (常数),存在一个非负局部可积函数
(常数),存在一个非负局部可积函数 满足:
满足:
 (6)
(6)
那么一定有
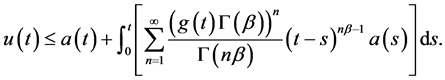 (7)
(7)
注1. 如果引理1中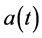 在
在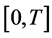 上满足非负不减少,那么可以把结论简化为
上满足非负不减少,那么可以把结论简化为 。
。
引理2. 如果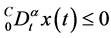 ,那么
,那么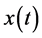 在
在 上单调减少;同理
上单调减少;同理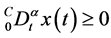 ,则
,则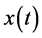 在
在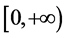 上单调增加。
上单调增加。
证明:只需证明引理的前半部分,后半部分证明思路同理。因为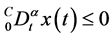 ,所以一定存在非负可积函数
,所以一定存在非负可积函数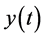 使得
使得
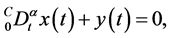
 (8)
(8)
对(8)式两边同时取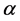 阶积分
阶积分 可得
可得
 (9)
(9)
若有 时,有
时,有 ,这也就证明了
,这也就证明了 在
在 上单调减少。
上单调减少。
引理2证毕。
引理3. 设 且具有连续的一阶导数,则
且具有连续的一阶导数,则
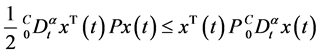 (10)
(10)
其中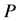 为任意的
为任意的 阶正定矩阵。
阶正定矩阵。
3. 主要结果
3.1. 有限时间稳定性分析
定理1. 考虑系统(1),对给定初始时刻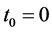 ,若存在Lyapunov函数
,若存在Lyapunov函数 ,
, 为定义在
为定义在 上的非负不减少连续函数,
上的非负不减少连续函数,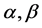 为两个
为两个 -类函数,若满足:
-类函数,若满足:
(1) 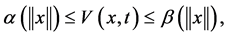
(2) 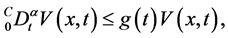
(3) 
那么系统(5)关于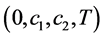 有限时间稳定。
有限时间稳定。
证明:对条件(2)两边同时取 阶积分
阶积分
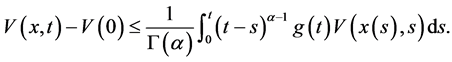 (11)
(11)
其中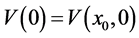 ,对(11)式两边同时乘以
,对(11)式两边同时乘以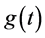

令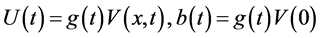 可得
可得
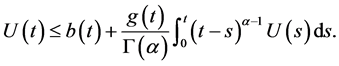 (12)
(12)
由引理1可得

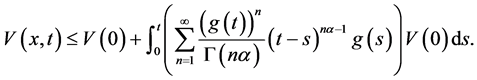 (13)
(13)
若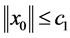 ,由条件1可知
,由条件1可知 ,代入(13)式可得
,代入(13)式可得
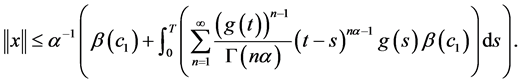
由条件(3)可得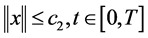 ,定理1证毕。
,定理1证毕。
推论1. 同样考虑系统(5),对给定初始时刻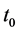 ,若存在Lyapunov函数
,若存在Lyapunov函数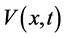 ,
, 为定义在
为定义在 上的非负不减少连续函数,
上的非负不减少连续函数, 为两个
为两个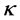 -类函数,若满足
-类函数,若满足
(1) 满足定理1的条件(1),(2),
(2) 。
。
其中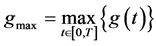 。则系统(5)关于
。则系统(5)关于 有限时间稳定。
有限时间稳定。
证明:由注2和(13)式可得

若满足 ,根据条件(2)易得
,根据条件(2)易得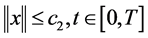 。推论1证毕。
。推论1证毕。
注2 文献 [2] [3] [4] 在研究分数阶非线性系统Lyapunov稳定时,需要其Lyapunov函数单调减少(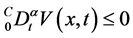 ),但是从定理1和推论1中可以发现,在分数阶系统有限时间稳定性分析中并不需要其满足此类条件,这也是分数阶系统有限时间稳定和Lyapunov稳定的不同之处。
),但是从定理1和推论1中可以发现,在分数阶系统有限时间稳定性分析中并不需要其满足此类条件,这也是分数阶系统有限时间稳定和Lyapunov稳定的不同之处。
3.2. 同步控制器设计
考虑分数阶驱动混沌系统和响应混动系统分别为:
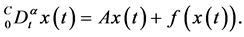 (14)
(14)
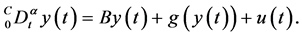 (15)
(15)
注3. 目前存在的大部分分数阶非线性混沌系统都可以表示为(14)式,如分数阶统一系统,分数阶Rossler系统等。
定义同步误差 ,本文的主要目标是设计合适的系统控制输入
,本文的主要目标是设计合适的系统控制输入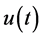 ,使得误差系统关于
,使得误差系统关于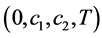 有限时间稳定。
有限时间稳定。
由系统(14)(15)得同步误差动态方程
 (16)
(16)
其中 。
。
为了完成两个分数阶混沌系统有限时间同步,可以设计如下控制器
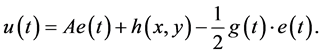 (17)
(17)
其中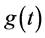 为定义在
为定义在 上的非负不减少连续函数。
上的非负不减少连续函数。
定理2对于给定初始时刻 ,在同步控制器(17)的作用下可实现驱动系统(14)和响应系统(15)关于
,在同步控制器(17)的作用下可实现驱动系统(14)和响应系统(15)关于 有限时间同步。
有限时间同步。
证明:将控制器(17)代入同步误差方程(16)可得
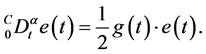
取Lyapunov函数为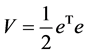 ,并对其两边同时取
,并对其两边同时取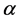 阶导数
阶导数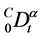 得
得
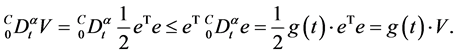
由推论1可知误差系统关于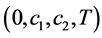 有限时间稳定。
有限时间稳定。
定理2证毕。
4. 数值仿真
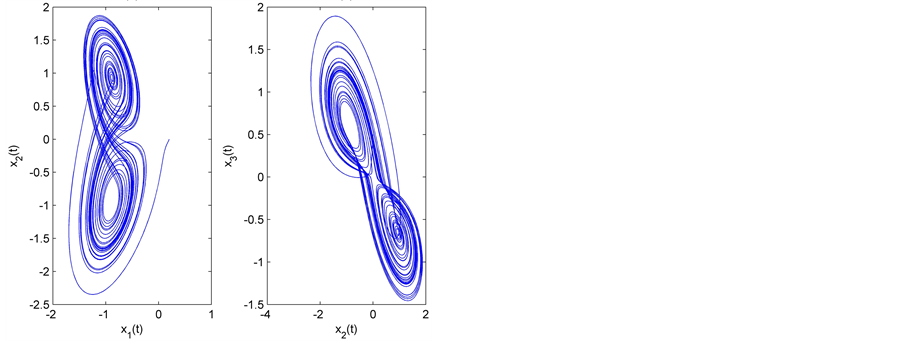
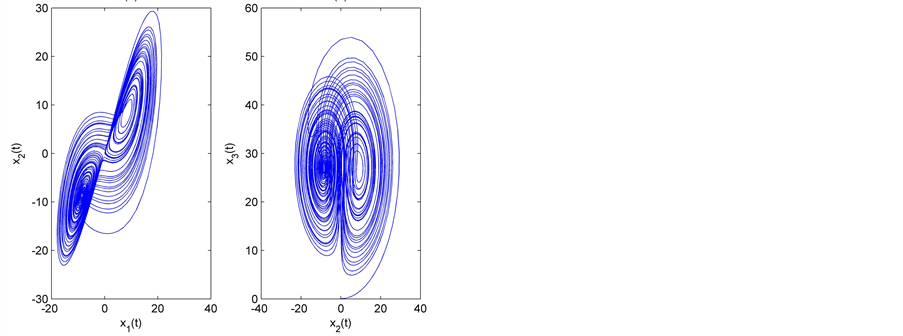
仿真中驱动系统设为分数阶Liu系统(图1),响应系统设为分数阶Lorenz系统(图2)。对应的线性部分系数矩阵和非线性部分分别为
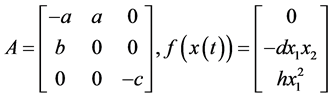 ,
,
任意选取初值分别为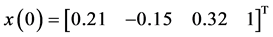 ,
,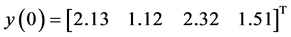 ,取
,取 ,
,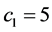 ,
,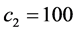 ,
, 在
在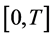 上构造
上构造 ,即
,即 ,通过计算可满足推论1的所有条件,由定理2可知误差系统关于
,通过计算可满足推论1的所有条件,由定理2可知误差系统关于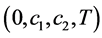 有限时间稳定。仿真结果如图3,图4所示,响应系统和驱动系统实现了有限时间同步。
有限时间稳定。仿真结果如图3,图4所示,响应系统和驱动系统实现了有限时间同步。
 (a)(b)
(a)(b)
Figure 1. Fractional order chaotic Liu system 
图1. 分数阶Liu混沌系统
 (a) (b)
(a) (b)
Figure 2. Fractional order chaotic Lorenz system 
图2. 分数阶Lorenz混沌系统
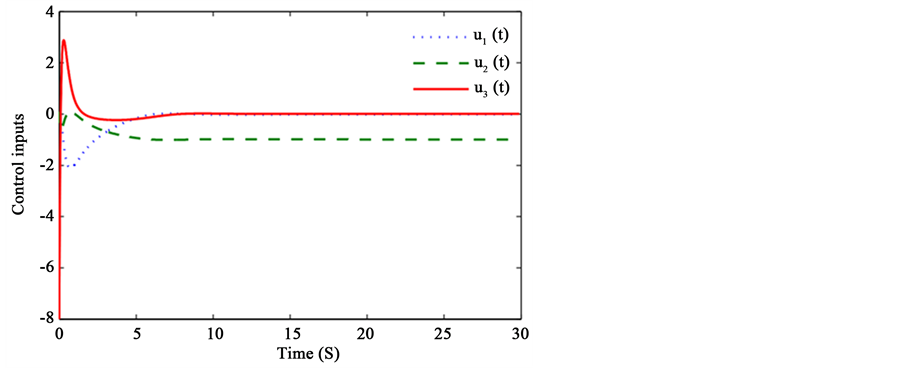
Figure 3. The curve of control inputs
图3. 控制输入曲线
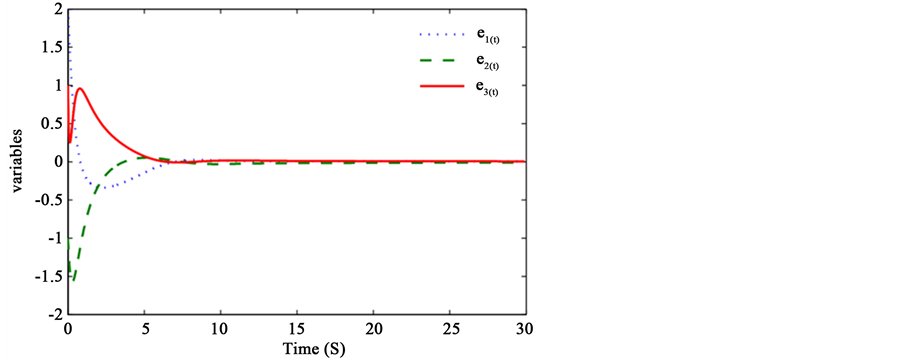
Figure 4. The curve of synchronization error
图4. 同步误差曲线图
5. 结论
本文研究了分数阶混沌系统有限时间稳定性及其同步控制,通过函数构造提出了分数阶混沌系统有限时间稳定性理论。基于该理论设计了主动控制器,在满足系统所有变量有界的情况下,实现了分数阶Liu系统与分数阶Lorenz系统异结构有限时间同步,从数值仿真可以看出误差系统能够在有限时间内稳定。该理论的研究有助于掌握分数阶混沌系统的相关性质,且同步控制方法也具有良好的鲁棒性能。本方法仍需进一步改进,针对不同的分数阶控制效果可能出现差异,带未知扰动或更严格的控制输入条件下(死区等)实现同步控制也需要进一步研究。
文章引用
刘丹丹,高彩霞. 分数阶混沌系统有限时间稳定性分析及同步控制
Analysis of Finite-Time Stability of Fractional-Order Chaotic System and Its Synchronization Control[J]. 理论数学, 2017, 07(03): 168-175. http://dx.doi.org/10.12677/PM.2017.73022
参考文献 (References)
- 1. Podlubny, I. (1999) Fractional Differential Equations. Academic Press Publishers, New York.
- 2. Li, Y., Chen, Y.Q. and Podlubny, I. (2009) Mittag-Leffler Stability of Fractional Order Nonlinear Dynamic Systems. Automatica, 45, 1965-1969.
- 3. Matignon, D. (1996) Stability Results for Fractional Differential Equations with Applications to Control Processing. Computational Engineering in Systems Applications, 2, 963-968.
- 4. Li, C.P., Deng, W.H. and Xu, D. (2006) Chaos Synchronization of the Chua System with a Fractional Order. Physica A, 360, 171-185.
- 5. Kuntanapreeda, S. (2012) Robust Synchronization of Fractional-Order Unified Chaotic Systems via Linear Control. Computers and Mathematics with Applications, 63, 183-190.
- 6. Chen, L.P., Chai, Y., Wu, R.C. and Yang, J. (2012) Stability and Stabilization of a Class of Nonlinear Fractional-Order Systems with Caputo Derivative. IEEE Transactions on Circuits and Systems-II: Express Briefs, 59, 602-606. https://doi.org/10.1109/TCSII.2012.2206936
- 7. Yin, C., Zhong, S.M. and Chen, W.F. (2012) Design of Sliding Mode Controller for a Class of Fractional-Order Chaotic Systems. Communications in Nonlinear Science and Numerical Simulation, 17, 356-366.
- 8. Wen, X.J., Wu, Z.M. and Lu, J.G. (2008) Stability Analysis of a Class of Nonlinear Fractional-Order Systems. IEEE Transactions on Circuits and Systems II: Express Briefs, 55, 1178-1182. https://doi.org/10.1109/TCSII.2008.2002571
- 9. Fallahi, K. and Leung, H. (2010) A Chaos Secure Communication Scheme Based on Multiplication Modulation. Communications in Nonlinear Science and Numerical Simulation, 25, 368-383.
- 10. Aghababa, M.P. (2014) A Lyapunov-Based Control Scheme for Robust Stabilization of Fractional Chaotic Systems. Nonlinear Dynamics, 78, 2129-2140. https://doi.org/10.1007/s11071-014-1594-8
- 11. Du, H.B., Cheng, Y.Y., He, Y.G. and Jia, R.T. (2014) Finite-Time Output Feedback Control for a Class of Second- Order Nonlinear Systems with Application to DC-DC Buck Converters. Nonlinear Dynamics, 78, 2021-2030. https://doi.org/10.1007/s11071-014-1593-9
- 12. Huang, L.L. and Ma, N. (2012) A New Method for Projective Synchronization of Different Fractional-Order Chaotic Systems. Acta Physica Sinica, 61, 160501-160506.
- 13. Rivero, M., Trujillo, J., Vazquez, L. and Velasco, M. (2011) Fractional Dynamics of Populations. Applied Mathematics and Computation, 218, 1089-1095.
- 14. 谭文, 李志攀, 王耀南, 等. 一个混沌系统的同步控制研究[J]. 计算机工程与应用, 2011, 47(4): 219-222.
- 15. 王兴元, 孟娟. 自治混沌系统的线性和非线性广义同步[J]. 物理学报, 2008, 57(2): 726-730.
- 16. 王兴元, 王勇. 基于线性分离的自治混沌系统的投影同步[J]. 物理学报, 2007, 56(5): 2498-2503.
- 17. 赵灵冬, 胡建兵, 刘旭辉. 参数未知的分数阶超混沌Lorenz系统的自适应追踪控制与同步[J]. 物理学报, 2010, 59(4): 2305-2309.
- 18. 赵建利, 王京, 王慧. 洛伦兹-哈肯激光混沌系统有限时间稳定主动控制方法研究[J]. 物理学报, 2011, 61(11): 110209.
- 19. Shen, J. and Lam, J. (2014) Non-Existence of Finite-Time Stable Equilibria in Fractional-Order Nonlinear Systems. Automatica, 50, 547-551.
- 20. 陈国培, 杨莹, 李俊民. 非线性系统有限时间稳定的一个新的充分条件[J]. 控制与决策, 2011, 26(6): 837-840.