Pure Mathematics
Vol.
09
No.
01
(
2019
), Article ID:
28377
,
5
pages
10.12677/PM.2019.91007
Function Characterizations of Some Spaces with Compact Gδ-Property
Congcong Wu
School of Mathematics & Physics, Anhui University of Technology, Ma’anshan Anhui

Received: Dec. 12th, 2018; accepted: Jan. 1st, 2019; published: Jan. 9th, 2019

ABSTRACT
Real-valued functions are useful tools for the characterizations of some topological spaces. Many classes of spaces can be characterized with real-valued functions that satisfy certain conditions, such as stratifiable spaces, k-semi-stratifiable spaces, etc. In this paper, we present some characterizations of spaces with compact Gδ-property in terms of real-valued functions, such as γ-spaces, c-stratifiable spaces, kc-stratifiable spaces, etc. The results obtained generalize some corresponding results for stratifiable spaces, k-semi-stratifiable spaces in the literature.
Keywords:γ-Spaces, C-Stratifiable Spaces, Kc-Stratifiable Spaces, Semi-Continuous Functions
某些具有紧-Gδ性质的空间的函数刻画
吴聪聪
安徽工业大学,数理科学与工程学院,安徽 马鞍山

收稿日期:2018年12月12日;录用日期:2019年1月1日;发布日期:2019年1月9日

摘 要
实值函数是刻画某些拓扑空间的有用工具,许多空间类都可以用满足一定条件的实值函数刻画,如:层空间、k-半层空间等。本文利用实值函数给出了某些具有紧-Gδ性质的空间的函数刻画,如:γ-空间、c-层空间、kc-半层空间等,推广了已有文献中关于层空间,k-半层空间等的一些结果。
关键词 :γ-空间,C-层空间,Kc-半层空间,半连续函数

Copyright © 2019 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 前言
本文提到的空间均为 空间,用 表示正整数集。空间X上的实值函数f称为下半连续(上半连续) [1] ,如果对任意实数 ,集合 为开集。记 为X到闭区间[0, 1]上所有下半连续(上半连续)函数的集合。
设X为拓扑空间,用 表示X上的拓扑, 为X的所有闭集构成的集族, 表示X的所有紧集的集族。设 ,记 为A的特征函数。
设f为半连续函数,在什么条件下存在连续函数列
使得这一
问题称为实值函数的函数列逼近问题。Tong在文献 [2] 证明了空间X是完备正规当且仅当对X上的任意下半连续函数f,存在X上的递增连续函数列
使得
。张国芳在文献 [3] 证明了空间X是k-半层空间当且仅当对每一
,存在递增函数列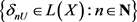 满足
;若
且
,则对每一
,
;对每一紧集
,U为开集且
,则存在
使得对任意
有
。完备正规空间,k-半层空间均为具有闭-
性质的空间,由于具有紧-
性质的空间与具有闭-
性质的空间在结构上相似,一个自然的问题是具有紧-
性质的空间是否也有类似的函数刻画。给出某些具有紧- Gδ 性质空间如
-空间、c-层空间、kc-半层空间的函数刻画。
满足
;若
且
,则对每一
,
;对每一紧集
,U为开集且
,则存在
使得对任意
有
。完备正规空间,k-半层空间均为具有闭-
性质的空间,由于具有紧-
性质的空间与具有闭-
性质的空间在结构上相似,一个自然的问题是具有紧-
性质的空间是否也有类似的函数刻画。给出某些具有紧- Gδ 性质空间如
-空间、c-层空间、kc-半层空间的函数刻画。
设X为拓扑空间,若映射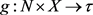 ,满足:对每一
及
,
;
;则称g为X上的一个g-函数。对于一个子集
,
。
,满足:对每一
及
,
;
;则称g为X上的一个g-函数。对于一个子集
,
。
定义1.1 [4] :空间X称为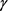 -空间。若存在X上的g-函数g,使得若对每一
,
且
,则
为
的聚点。
-空间。若存在X上的g-函数g,使得若对每一
,
且
,则
为
的聚点。
定义1.2 [5] :空间X称为c-半层空间(c-层空间)。若存在X上的g-函数g,使得对每一
,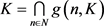 (
)。
(
)。
定义1.3 [6] :空间X称为kc-半层空间。若存在g-函数g,使得对任意
且
,则存在
使得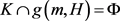 。
。
2. 主要结果
本节中,我们将利用实值函数给出 -空间,c-层空间,kc-半层空间的若干等价刻画。
引理2.1 [7] :X为 -空间当且仅当存在X上的g-函数g使得若 , 且 ,则存在 使得 。
定理2.2:X为
-空间当且仅当对每一
,存在递减函数列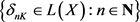 满足
满足
(1) ;
(2) 若 且 ,则对每一 , ;
(3) 对每一紧集
及
且
,存在
使得对任意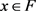 有
。
有
。
证:设 为 -空间,g为引理2.1中的g-函数,对每一 及 ,令 ,则 关于n递减且 。
(1) 设
,对每一
,若
,则对每一
,
,于是
;若
,则存在
使得
,于是当
时,有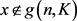 ,故
。
,故
。
(2) 设 且 ,则对每一 ,有 ,由此可得 。
(3) 设
,
且
,由引理2.1,存在
使得 ,故对任意
,有
,则
。
,故对任意
,有
,则
。
反之,对每一
及
,令
。由(1),对每一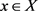 ,有
,故存在
使得对任意
,
。由于
关于n递减,故对每一
,
,则
。显然对每一
及
,有
,故g为X上的g-函数。
,有
,故存在
使得对任意
,
。由于
关于n递减,故对每一
,
,则
。显然对每一
及
,有
,故g为X上的g-函数。
对每一 及 ,令 。设 ,则存在 使得 ,则 ,由条件(2)得 ,故 ,这表明 。设 , 且 K ∩ H = Φ ,由条件(3),存在 使得对任意 有 ,故 ,从而 。由引理2.1, 为 -空间。
定理2.3:X为 -空间当且仅当对每一 ,存在递减函数列 满足:
(1) 对每一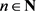 及
,若
,则
;
及
,若
,则
;
(2) 若
且
,则对每一
,有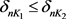 ;
;
(3) 若 , 且 ,则 在 上一致收敛于0。
证:设 为 -空间,g为引理2.1中的g-函数,对每一 及 ,令 则 关于 递减且 。(1),(2)显然成立。
(3)设
,
且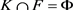 ,由引理2.1,存在
使得
。对
,当
时,对任意
有
,故
,这说明
在
上一致收敛于0。
,由引理2.1,存在
使得
。对
,当
时,对任意
有
,故
,这说明
在
上一致收敛于0。
反之,对每一
及
,令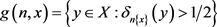 。由(1)知,每一
及
,
,又
,故g为X上的g-函数。对每一
及
,令
,由定理2.2的充分性的证明知
。设
,
。由(1)知,每一
及
,
,又
,故g为X上的g-函数。对每一
及
,令
,由定理2.2的充分性的证明知
。设
,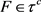 且
,由条件(3),
在
上一致收敛于0,则存在
,对任意
,有
,于是
,故
,则X为
-空间。
且
,由条件(3),
在
上一致收敛于0,则存在
,对任意
,有
,于是
,故
,则X为
-空间。
定理2.4:X为正则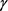 -空间当且仅当对每一
,存在递减函数列
-空间当且仅当对每一
,存在递减函数列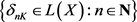 ,满足:
,满足:
(1) ;
(2) 若 且若 ,则对每一 ,有 ;
(3) 若
,
且
,则存在开集
及
使得对任意
有
。
证:设
为
-空间,g为引理2.1中的g-函数,对每一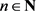 及
及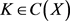 ,令
,则
关于
递减且
δnk ∈L (X) 。(1) (2)的证明同定理2.2。设
,
且
,由于
为正则空间,故X的无交开集U,V使得
,存在
使得
,则
,故对任意一
,有
。
,令
,则
关于
递减且
δnk ∈L (X) 。(1) (2)的证明同定理2.2。设
,
且
,由于
为正则空间,故X的无交开集U,V使得
,存在
使得
,则
,故对任意一
,有
。
反之,由定理2.2知X为
-空间,下证
为正则空间。对每一
及
,令
。设
,由(3)得,存在开集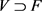 及
使得对任意
,
,则
,故
及
使得对任意
,
,则
,故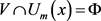 ,这说明
为正则空间。
,这说明
为正则空间。
定理2.5:X为c-层空间当且仅当对每一 ,存在递减函数列 及 满足:
(1) ;
(2) 若
且
,则对每一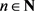 ,
;
,
;
(3) 对每一 及 , 。
证:设 为X的c-层函数,对每一 及 ,令 , ,则 关于n递减且 。(2) (3)显然成立。
(1) 设
,若
,则
,则对每一
,有
,则
;若
,则
,故存在
使得对任意
,有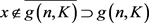 ,于是
。
,于是
。
反之,对每一
及
,令
,则g为X上的g-函数。对每一
及
,令
,则
。设
,则存在
使得
。由条件(2),(3)得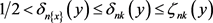 ,故
,这表明
,故
。
,故
,这表明
,故
。
设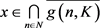 ,则对每一
,
,则
,故
,则对每一
,
,则
,故
,这说明
,于是
。故
为c-层空间。
定理2.6:X为kc-半层空间当且仅当对每一
K ∈C(x) ,存在递减函数列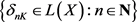 满足
满足
(1) 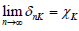 ;
;
(2) 若 且 ,则对每一 ,有 ;
(3)若 且 ,则存在 使得对任意 有 。
证:设g为kc-半层函数,对每一 及 ,令 ,则 关于 递减且 。(1) (2)的证明同定理2.2。设 且 ,则存在 使得 ,故对任意 , 。
反之,对每一
及
,令
,则g为X上的g-函数。对每一
及
,令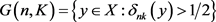 ,则
。设
且
,由条件(3),存在
使得对任意
,则
。设
且
,由条件(3),存在
使得对任意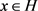 有
,故
,从而
。故
为kc-半层空间。
有
,故
,从而
。故
为kc-半层空间。
由定理2.2的证明可得:
定理2.7:X为kc-半层空间当且仅当对每一 ,存在递减函数列 满足
(1) 对每一 及 ,若 ,则 ;
(2) 若 且 ,则对每一 ,有 ;
(3) 若 ,且 ,则 在 上一致收敛于0。
由定理2.5的证明可得:
命题2.8:X为c-半层空间当且仅当对每一 K ∈C(x),存在递减函数列 满足
(1) ;
(2) 若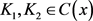 且
,则对每一
,有
。
且
,则对每一
,有
。
文章引用
吴聪聪. 某些具有紧-Gδ性质的空间的函数刻画
Function Characterizations of Some Spaces with Compact Gδ-Property[J]. 理论数学, 2019, 09(01): 49-53. https://doi.org/10.12677/PM.2019.91007
参考文献
- 1. Engelking, R. (1977) General Topology. Polish Scientific Publishers, Warszawa.
- 2. Tong, H. (1952) Some Characterizations of Normal and Perfectly Normal Spaces. Duke Mathematical Journal, 19, 289-292.
https://doi.org/10.1215/S0012-7094-52-01928-5 - 3. 张国芳, 杨二光. k-半层空间的函数刻画[J]. 山东大学学报(理学报), 2006, 26(2): 213-218.
- 4. Hodel, R.E. (1972) Hodel, Spaces Defined by Sequence of Open Covers Which Guarantee that Certain Sequences Have Cluster Points. Duke Mathematical Journal, 39, 253-263.
https://doi.org/10.1215/S0012-7094-72-03930-0 - 5. Martin, H.W. (1973) Metrizability of M-Spaces. Canadian Journal of Mathematics, 25, 840-841.
https://doi.org/10.4153/CJM-1973-086-0 - 6. Martin II, H.W. (1973) Metrization and Submetrization of Topological Spaces. Ph D Thesis, University of Pittsburgh, Pittsburgh, PA.
- 7. Lindgren, W.F. and Fletcher, P. (1974) Locally Quasi-Uniform Spaces with Countable Bases. Duke Mathematical Journal, 41, 231-240.
https://doi.org/10.1215/S0012-7094-74-04125-8