Pure Mathematics
Vol.
09
No.
05
(
2019
), Article ID:
31402
,
10
pages
10.12677/PM.2019.95080
Local Lorentz Estimates for the Bi-Harmonic Parabolic Equation
Jiayi Zhu
College of Sciences, Shanghai University, Shanghai
Received: Jun. 30th, 2019; accepted: Jul. 18th, 2019; published: Jul. 25th, 2019

ABSTRACT
Lp estimates are the basic regularity estimates in the partial differential equations. In this paper, we mainly study a new class of regularity estimates—Lorentz estimates for the Bi-harmonic parabolic equation.
Keywords:Bi-Harmonic Parabolic Equation, Regularity Estimates, Lorentz Space
双调和抛物方程解的局部Lorentz估计
朱加义
上海大学理学院,上海
收稿日期:2019年6月30日;录用日期:2019年7月18日;发布日期:2019年7月25日

摘 要
Lp估计是偏微分方程中基本的正则性估计,本文我们主要研究一类四阶双调和抛物方程的解的新的正则性估计——Lorentz估计。
关键词 :双调和抛物方程,正则性估计,Lorentz空间

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
微分方程解的存在唯一性及其正则性研究是偏微分方程中的经典问题,其中
估计在正则性理论的研究中具有非常重要的作用。2003年,Wang [1] 在Caffarelli和Peral [2] 基础上利用紧方法、Vitali覆盖引理、极大函数等技巧给出了Possion方程和热传导方程的内估计的几何化证明方法。之后,Byun和Wang利用类似技巧在 [3] [4] [5] [6] [7] 中得到了各类二阶散度型椭圆方程与抛物方程在不同区域中的估计。2013年,Baroni在 [8] 中证明了退化的和非退化的具有VMO系数的散度型椭圆和抛物方程组在Lorentz空间中的正则性估计。在那篇文章中,Baroni引入了Calderón-Zygmund算子和相应的水平估计得到了文章的结论。另外,Yao和Zhou在 [9] [10] 中又给出了一类四阶双调和抛物方程解的
和Schauder估计。2015年,Yu在 [11] 中证明了这类四阶双调和抛物方程的加权
估计。本文主要研究下述四阶双调和抛物方程解的局部Lorentz估计
(1)
这里我们定义
,
,其中
。另外我们记
本文的主要目的是得到问题(1)的解u的如下估计
其中
与u和f无关。
下面给出Lorentz空间 [8] 的定义和嵌入性质。对于开集
和参数
,
,Lorentz空间
是包含所有满足下式的可测函数
组成的空间
事实上,当
,Marcinkiewicz空间
,且有
性质1 [8] :对于
和
,有以下连续嵌入成立
(2)
且有
。
性质2 [8] :对于
和
,有以下连续嵌入成立
(3)
且有
。
下面我们给出本文所要证明的主要结论。
定理3:对于
,
。假设
,
。如果u满足双调和抛物方程(1)且
,那么就有
,且有以下估计式成立
(4)
其中常数
与u和f无关。
2. 引理和准备工作
引理4 [12] :Hardy不等式:可测函数
使得
那么对于任意
和
都有
引理5 [13] :反Hölder不等式:
是一个不增可测函数,其中
,
。那么当
时
对每个
和任意
;如果
那么
常数c依赖于
,
,r。当
时,常数
。
引理6 [14] :迭代引理:设
,
是
上的有界非负函数,且对于任意的
,
满足
其中
,A,B和
是非负常数,且
,则
对任意
,其中常数
。
引理7 [15] :Hölder不等式:如果
,那么
,
且有以下不等式成立
下面我们给出证明定理3之前所需的准备工作。
令
其中
,
。
定义Calderón-Zygmund算子为
其中
且
。令
,则对于固定的
,
,我们将积分区域从
扩大到
,就有
现在对于点
的水平集
,由Lebesgue定理可得
,当
。因此,一旦固定
,由积分的绝对连续性可知存在最大的
使得
(5)
其中
且对任意的
,有
(6)
现令
,那么对于固定的
,那么必有以下式子中的其中一个成立
或
(7)
假设第一种情况成立,那么我们得到
吸收右端第一项就有
(8)
另一方面,如果第二种情况成立,那么选取
,分离积分得到
吸收右端第一项可得
(9)
结合式(8)和(9),我们就有
(10)
令
,
。事实上,根据式(6)可得如下两个不等式
(11)
(12)
对于固定的
,我们首先对
作从
到
上的零延拓,并记为
。则
,现在我们引入下述参照方程
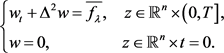
由
估计 [9] ,我么可得:
。从而可得
由上式及式(12)得
(13)
令
,可知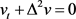 ,
。
,
。
由式(11)和(13)得
故由基本的
内部正则性理论,可得:
,这里取
。
对任意的
,因此
,故有
。再对于任意的
,结合式(12)得到
(14)
下面考虑式(5),根据Vitali覆盖引理,可知存在一族互不相交的
,
且
。再由式(10)和(14)得到
. (15)
3. 定理3的证明
下面证明当
时的结论。
对于
和
,首先根据Lorentz范数的定义得到
对于
,考虑
的定义和不等式
(见引理7)和
(见式3),我们有
(16)
对于
,结合式(15)有
(17)
进一步,当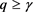 时,利用引理4得到
时,利用引理4得到
(18)
当
,利用引理5
得到
因此,再利用Fubini定理我们有
(19)
同理可得
(20)
因此,由式(18),(19)和(20)我们有
最后结合估计式
和
,可以得到
不妨假设
。事实上,考虑截断梯度
。然后选择M充分大,
再利用迭代引理就可以得到当
时的结论。
下面证明当
时的结论。
考虑式(7)中的第二种情形,
为一个待定常数,有
接下来,利用引理7,定义
,那么
选择适当的
使得
,事实上
,那么
(21)
同样的,根据(7)式中的第一种情形我们可以得到
(22)
其中
。因此,结合以上两式得到
类似于在式(15)中的做法,由Vitali覆盖引理我们得到
(23)
下面根据范数定义,我们有
先估计
,考虑
的定义和不等式
(见引理7),得到
(24)
对于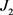 ,考虑式(23),进行变量替换之后得到
,考虑式(23),进行变量替换之后得到
(25)
因为
,
。最后,结合估计
式
和
我们得到
因此,类似于在
中的情形,利用迭代引理我们就得到了当
时的结论。
综上所述,定理3得证。
致谢
首先我要感谢我的导师姚锋平老师,在老师一直的鼓励和无私的指导之下我才能够完成本篇论文的写作。其次,我要感谢我同师门的师姐,她们在我的论文写作过程中给出了宝贵的建议。最后,我要感谢我的父母对我学业上的支持。
文章引用
朱加义. 双调和抛物方程解的局部Lorentz估计
Local Lorentz Estimates for the Bi-Harmonic Parabolic Equation[J]. 理论数学, 2019, 09(05): 601-610. https://doi.org/10.12677/PM.2019.95080
参考文献
- 1. Wang, L. (2003) A Geometric Approach to the Calderón-Zygmund Estimates. Acta Mathematica Sinica, 19, 381-396.
https://doi.org/10.1007/s10114-003-0264-4
- 2. Caffarelli, L. and Peral, I. (1998) On Estimates for Elliptic Equations in Divergence Form. Communications on Pure and Applied Mathematics, 51, 1-21.
https://doi.org/10.1002/(SICI)1097-0312(199801)51:1<1::AID-CPA1>3.0.CO;2-G
- 3. Byun, S. and Wang, L. (2004) Elliptic Equations with BMO Coefficients in Reifenberg Domains. Communications on Pure and Applied Mathematics, 57, 1283-1310.
https://doi.org/10.1002/cpa.20037
- 4. Byun, S. and Wang, L. (2005) Estimates for Parabolic Equations in Reifenberg Domains. Journal of Functional Analysis, 223, 44-85.
https://doi.org/10.1016/j.jfa.2004.10.014
- 5. Byun, S. and Wang, L. (2005) Parabolic Equations in Reifenberg Domains. Archive for Rational Mechanics and Analysis, 176, 271-301.
https://doi.org/10.1007/s00205-005-0357-6
- 6. Byun, S. and Wang, L. (2007) Parabolic Equations in Time Dependent Rei-fenberg Domains. Advances in Mathematics, 212, 797-818.
https://doi.org/10.1016/j.aim.2006.12.002
- 7. Byun, S. and Wang, L. (2007) Quasilinear Elliptic Equations with BMO Coefficients in Lipschitz Domains. Transactions of the American Mathematical Society, 359, 5899-5913.
https://doi.org/10.1090/S0002-9947-07-04238-9
- 8. Baroni, P. (2013) Lorentz Estimates for De-generate and Singular Evolutionary Systems. Journal of Differential Equations, 255, 2927-2951.
https://doi.org/10.1016/j.jde.2013.07.024
- 9. Yao, F.P. and Zhou, S.L. (2008) Global Estimates for the Parabolic Equa-tions of the Bi-Harmonic Type. Journal of Partial Differential Equations, 21, 315-334.
- 10. Yao, F.P. and Zhou, S.L. (2007) Schauder Estimates for the Bi-Harmonic Parabolic Equation. Applied Mathematics and Mechanics, 11, 1340-1352.
https://doi.org/10.1007/s10483-007-1110-z
- 11. Yu, H.C. (2015) Weighted Estimates for the Bi-Harmonic Parabolic Equation. Pure Mathematics, 5, 46-53.
https://doi.org/10.12677/PM.2015.52007
- 12. Hardy, G.H., Littlewood, J.E. and Polya, G. (1952) Inequalities. Cambridge University Press, Cambridge.
- 13. Stein, E.M. (1970) Singular Integrals and Differentiability Properties of Functions. Princeton University Press, Princeton, NJ.
https://doi.org/10.1515/9781400883882
- 14. 伍卓群, 尹景学, 王春朋. 椭圆与抛物型方程引论[M]. 北京: 科学出版社, 2003.
- 15. Mingione, G. (2007) The Calderón-Zygmund Theory for the Elliptic Problems with Measure Data. Annali della Scuola Normale Superiore di Pisa, 6, 195-261.





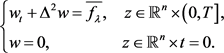
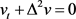 ,
。
,
。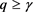 时,利用引理4得到
时,利用引理4得到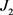 ,考虑式(23),进行变量替换之后得到
,考虑式(23),进行变量替换之后得到