Pure Mathematics
Vol.
09
No.
08
(
2019
), Article ID:
32571
,
8
pages
10.12677/PM.2019.98117
The Action of the Bessel Potentials on Space
Renkun Shi
Department of Mathematics, College of Science, Hohai University, Nanjing Jiangsu

Received: Sep. 23rd, 2019; accepted: Oct. 10th, 2019; published: Oct. 17th, 2019

ABSTRACT
In this paper, we concern the action of the Bessel potentials on space with . By the method of contradiction, we prove that for any , the Bessel potential cannot be a bounded linear operator from to , and obtain other related results.
Keywords:Bessel Potentials, Space, Unbounded Operators

Bessel位势在空间 上的作用
史仁坤
河海大学,理学院数学系,江苏 南京

收稿日期:2019年9月23日;录用日期:2019年10月10日;发布日期:2019年10月17日

摘 要
本文对Bessel位势在线性空间 上的作用进行了研究。利用反证法证明了对任意的 ,任一Bessel位势都不可能是 到 上的有界线性算子,并得到了其他相关的结论。
关键词 :Bessel位势, 空间,无界算子

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在非线性偏微分方程问题,特别是大初值问题中,最难处理的项往往是非线性项。因此如何得到关于非线性项的良好估计就成为一个不可避免的重要问题。在处理非线性项的过程中,我们经常会运用各种Sobolev嵌入定理以及不等式,其中一个常用不等式是Hölder不等式 [1] :
(1)
其中
(2)
是一区域。值得指出的是,只要 满足(2)式,则(1)式对任意的 和 都成立。特别地,当 , 且
(3)
时,有 。此时由于 ,空间 并不在我们通常所考虑的空间之列,因为在
这类空间中,很多不等式,如Minkowski不等式,不再成立 [1]。由此引出一个问题,即当 , 且满足(3)式时,能否找到算子A以及常数 ,使得
? (P)
换言之,能否找到算子A,使得A(uv)具有相比于uv而言更高的正则性?这是一个很宽泛的问题。为了便于讨论,本文仅考虑 的情形,并且只对一类算子——Bessel位势进行研究。
Bessel位势是形如
的拟微分算子,其核函数为
(4)
该核函数的Fourier变换为
从而对任意 ,都有
(5)
这部分内容可参见 [2] 的第五章第3.1节。Bessel位势具有很好的正则效应。事实上,我们有下面这个性质。
性质1.1 对 ,若 ,则
(6)
性质1.1意味着当 足够大时, 具有比u更高的正则性。这促使我们去考虑问题(P)在算子A是Bessel位势时的情形。具体而言,我们考虑下述问题,即当 且 满足 (3)
式时(此时 且 ),能否找到 ,使得
(7)
成立?
以上就是本文对Bessel位势在线性空间 上的作用进行研究的具体原因。通过一些构造性的证明,本文从反面给出了上述问题的否定回答。
记号 在以下叙述中,我们简记
主要结论如下。
定理1.1 设 ,则对任意 ,都不存在连续函数 ,使得
(8)
定理1.2 设 ,则对任意 ,都不存在连续函数 ,使得
(9)
定理1.3 设 且 ,则对任意 ,都不存在连续函数 ,使得
(10)
定理1.4 设 且 ,则对任意 ,都不存在连续函数 ,使得
(11)
注:为保证定理中的 和 有意义,可以限制 都是速降函数。事实上,在定理证明过程中所构造的函数都是速降函数。
上述结论给出了问题(7)的否定回答。从定理1.1可以看出,当 时,对任意 ,Bessel位势 都不可能是 到 上的有界线性算子。这一点与性质1.1是大不相同的,反映出 空间与 空间具有本质上的区别。定理1.3则说明当
且 时,(7)式不可能成立,从而给出了问题的否定回答。定理1.2和定理1.4则说明,
时,(7)式不可能成立,从而给出了问题的否定回答。定理1.2和定理1.4则说明,
即使对函数u再加以其他空间上的限制,只要空间的正则性指标不够,我们仍得不到 或
或 的有界性估计。
的有界性估计。
需要注意的是,本文的结果仅仅是给出了问题(7)的否定回答,至于一般问题(P),算子A是否存在尚未可知,因此该问题还需作进一步的研究。
上述定理以及性质1.1的证明将在第2节给出。
2. 定理的证明
定理1.1的证明:对任意 ,令
,令

显然

下面用反证法完成证明。假设存在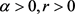 以及连续函数
以及连续函数 ,使得(8)式成立,则必有
,使得(8)式成立,则必有
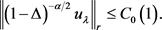 (12)
(12)
另一方面,由 和
和 的非负性知
的非负性知
 (13)
(13)
此外,由(4)式知当 时,有
时,有
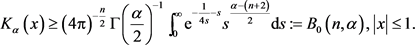 (14)
(14)
故当 时,有
时,有
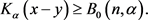 (15)
(15)
由(13)和(15)知当
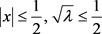
时,有
 (16)
(16)
其中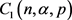 是依赖于
是依赖于 的常数。注意到
的常数。注意到
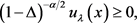
由(16)式可得
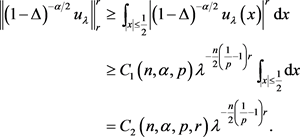 (17)
(17)
在(17)式中令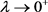 ,并利用条件
,并利用条件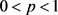 ,可得
,可得

这与(12)式矛盾,故假设不成立,定理得证。
定理1.2的证明:对任意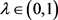 ,令
,令

则有

由此可得
 (18)
(18)
其中最后一个不等式中利用了 和
和 这两个事实。记
这两个事实。记

其中 是一个依赖于
是一个依赖于 的非负函数。由(18)式知,
的非负函数。由(18)式知, 在
在 时一致有界。令
时一致有界。令

易得
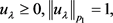 (19)
(19)
且
 (20)
(20)
下面用反证法完成证明。假设存在 以及连续函数
以及连续函数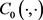 ,使得(9)式成立,则由(19)和(20)知
,使得(9)式成立,则由(19)和(20)知
 (21)
(21)
另一方面,由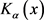 和
和 的非负性以及(14)式知,当
的非负性以及(14)式知,当 时,有
时,有
 (22)
(22)
由(22)式可得
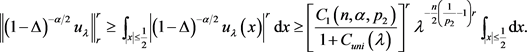
设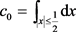 ,则
,则
 (23)
(23)
在(23)式中令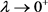 ,并利用条件
,并利用条件 ,可得
,可得
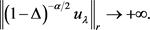
这与(21)式矛盾,故假设不成立,定理得证。
定理1.3的证明:(反证法)假设存在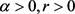 以及连续函数
以及连续函数 ,使得(10)式成立。记
,使得(10)式成立。记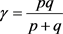 ,
,
由定理条件知,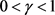 。现在任取
。现在任取
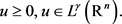 (24)
(24)
令 ,则
,则 。从而由(10)式知
。从而由(10)式知
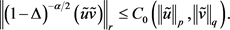
又

从而

上式对任意满足(24)式的函数都成立,其中 。这与定理1.1的结论相矛盾,故假设不
。这与定理1.1的结论相矛盾,故假设不
成立,定理得证。
定理1.4的证明:(反证法)假设存在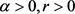 以及连续函数
以及连续函数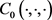 ,使得(11)式成立。记
,使得(11)式成立。记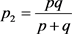
 ,由定理条件知,
,由定理条件知, 。现在任取
。现在任取
 (25)
(25)
令 ,则
,则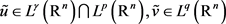 。从而由(11)式知
。从而由(11)式知

又
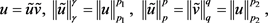
从而

上式对任意满足(25)式的函数都成立,其中 。这与定理1.2的结论相矛盾,故假设不成立,定理得证。
。这与定理1.2的结论相矛盾,故假设不成立,定理得证。
性质1.1的证明:任取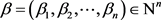 ,
,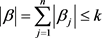 。由(5)式可得
。由(5)式可得

利用卷积形式的Young不等式,可得
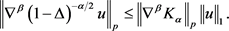 (26)
(26)
另一方面,由(4)式知

其中
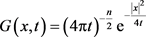
是热传导方程的Green函数。从而利用性质1.1的条件可得
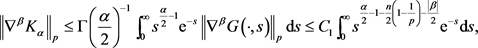
其中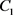 是常数。同时,由性质1.1的条件知
是常数。同时,由性质1.1的条件知

故存在常数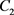 ,使得
,使得
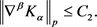 (27)
(27)
将(27)代入(26),有

进而可得
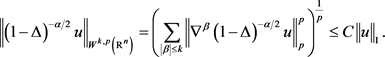
即(6)式成立,得证。
基金项目
江苏省自然科学基金(No. BK20160856)和国家自然科学基金(No. 11801137)。
文章引用
史仁坤. Bessel位势在空间Lp(Rn)(0 < p < 1)上的作用
The Action of the Bessel Potentials on Lp(Rn)(0 < p < 1) Space[J]. 理论数学, 2019, 09(08): 908-915. https://doi.org/10.12677/PM.2019.98117
参考文献
- 1. Adams, R.A. and Fournier, J.J.F. (2003) Sobolev Spaces. 2nd Edition, Academic Press, New York.
- 2. Stein, E.M. (1970) Singular Integrals and Differentiability Properties of Functions. Princeton University Press, Princeton. https://doi.org/10.1515/9781400883882