Pure Mathematics
Vol.
09
No.
10
(
2019
), Article ID:
33558
,
7
pages
10.12677/PM.2019.910143
Several Notes in the Teaching of Complex Functions
Rui Xu, Xiaorui Yue*
School of Information and Communication Engineering, Hainan University, Haikou Hainan

Received: Nov. 30th, 2019; accepted: Dec. 13th, 2019; published: Dec. 20th, 2019

ABSTRACT
The purpose of this paper is to give some remarks to the problems of finding the convergence radius of some special series, the anti-derivative of power function multiplying exponential function and the order of polar points in return to generalize some relating consequences in real functions and then bring convenience to calculations. In this paper, we give the general result of the anti-derivative of power function multiplying exponential function; we also expand the L’hospital’s rule to find the order of some special polar points and give the proof.
Keywords:Complex Functions, Radius of Convergence Series, Anti-Derivatives, L’Hospital’s Rule

复变函数教学中的几个注释
徐瑞,岳晓蕊*
海南大学信息与通信工程学院 理学院,海南 海口

收稿日期:2019年11月30日;录用日期:2019年12月13日;发布日期:2019年12月20日

摘 要
本文旨在对复变函数中求解特殊级数的收敛半径、幂函数乘指数函数原函数以及极点阶数等问题做一些补充说明,推广实函数中的相应结论,为计算带来方便。文中整理幂函数乘指数函数原函数的求解结果,并总结出统一的公式;求解极点阶数,推广实变函数中的洛必达法则以给出判断方法,并给予严格证明。
关键词 :复变函数,收敛半径,原函数,洛必达法则

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
复变函数的理论研究起源于十八世纪,是数学中一门古老又较为成熟的学科。其相关理论应用十分广泛,可以用来解决很多复杂的运算,比如物理学上有很多不同的稳定平面场的计算就是通过复变函数来解决的;此外,复变函数也应用于微分方程、积分方程、概率论和数论等学科,推动数学领域其他分支的发展。复变函数作为实函数的扩展,其相关计算性质与实函数既有相同之处,也有不同之处。比如实变函数中求收敛半径以及求解指数函数的原函数都可推广到复数领域,同时,与实函数不同的是,复变函数需要判断极点及其阶数。
本文旨在对复变函数中求解收敛半径、幂函数乘指数函数的原函数以及极点阶数等问题做一些补充说明。文中分析了收敛半径求解中的两种特殊情况;整理幂函数乘指数函数原函数的求解结果,并总结出统一的公式;求解极点阶数,推广实变函数中的洛必达法则以给出判断方法,并给予严格证明,从而推广实函数中的相应结论,为计算带来方便。
2. 两种级数收敛半径的求法
在众多教材中仅对一些常见的级数的收敛半径进行求解,而没有对一些特殊级数收敛半径的求解展开讨论。本节中,我们补充如下两种特殊类型的级数的收敛半径问题。
2.1. 含
的幂级数
首先考虑如下可分为两部分的幂级数
在求解较复杂的级数收敛半径时,我们需用以下结论,参考文献 [1] 和 [2] 中讨论了实数情况,我们将其中的证明过程做出对应的补充说明,也可得到类似结论。
引理1 [3] 设复幂级数
与复幂级数
的收敛半径分别为
与
,
的收敛半径为R,则
(i) 在
时,有
;
(ii) 在
时,有
。
对级数I的收敛问题我们有如下结论:
定理1
令
,,其中
与
均收敛,
。
若
,,且
。
则
的收敛半径
。
证明:
1) 当
时,
充分性:
由经典的比值法及参考文献 [4] 和 [5] 得知,
的收敛半径可由如下计算过程得出:
。
当
时,
收敛,
在圆
内收敛。
必要性
另一方面,当
时,可证级数发散。事实上,假设在圆外一点
处级数
收敛。在圆外再取一点
,使得
,则由阿贝尔定理知,级数
必收敛。然后因为
,有
,矛盾。
综上,当
时,
的收敛半径为
。
2) 当
时,
。
充分性:
的收敛半径可由如下计算过程得出:
。
当
时,
收敛,
在圆
内收敛。
必要性:
另一方面,当
时,可证级数发散。事实上,假设在圆外一点
处级数
收敛。在圆外再取一点
,使得
,则由阿贝尔定理可知级数
必收敛。然后因为
,有
,矛盾。
综上,当
时,
的收敛半径为
。
f(z)的收敛半径
。
2.2. 可变量代换的幂级数
(i) 定理2
,k和
若
,由经典的比值法可知,幂级数
的收敛半径为
。
(ii) 定理3
若
,则当
时,幂级数
收敛。
3. 幂函数乘指数函数的原函数
本节中我们考虑与指数函数有关的特殊类型函数的原函数,即
形式。
首先由分部积分公式,我们可以推导出如下结论:
(1)
(2)
(3)
3.1. 定理4
接下来,我们通过归纳法给出原函数结果的理论证明:
证明:当k=1,2,3时,由(1),(2),(3)可得命题成立,假设当
时命题也成立,即
当
时,
故当
时,假设仍然成立。
综上所述,当
时,有
3.2. 推广
定理4的证明使用了归纳法,下述结论使用了另一种证明办法,得到更一般的结果,当然这两种办法都适用。
定理5
证明:
总结得出如下结论:
(i)
为
;
(ii)
为
。
注释:上述结果,可作如下理解:
的结果一共有n + 1项,每一项正负交替,并且按照
的升幂顺序由
逐项升到
,z按照降幂顺序由zn逐项降到z0,n按照阶乘的形式逐项包括
,且各项包含指数项
。
4. 孤立奇点类型的判断
孤立奇点类型的判断是为了针对不同类别考虑如何求留数,从而计算积分。由定义知,可去奇点处对应的留数为0,本性奇点一般只能通过展开式求留数,所以重点考虑极点。其中,有如下结论:
定理A [6]
有h级极点z0的充要条件为:
,其中
在点z0处解析,且
。
当
不满足定理A中的情况时,我们有如下类似实函数中洛必达法则的办法判断极点阶数(参考文献 [7] )。
定理6 设
,其中g在z0处解析,且
,令
,则f与
的极点级数相同。特别地,当
是
的h − 1级极点,则
也是f的h − 1级极点,类似于实变函数中的洛必达法则。
证明:因为
解析,所以
,所以由洛必达法则知:
故f与
的奇点类型相同。
例:判断函数
的极点的级数。
解:因为
,所以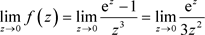 ,由定理5得
,由定理5得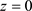 是
是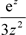 的2级极点,因此
的2级极点,因此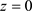 是
是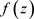 的2级极点。
的2级极点。
5. 结束语
本文对复变函数幂级数收敛半径的求解、幂函数乘指数函数的原函数以及极点阶数的判断问题进行整理和补充。在收敛半径求解问题中补充了在求解幂级数收敛半径中包含 复幂级数的收敛半径以及可变量代换求解幂级数的收敛域这两类问题;在求解指数函数原函数的问题中总结了
复幂级数的收敛半径以及可变量代换求解幂级数的收敛域这两类问题;在求解指数函数原函数的问题中总结了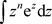 与
与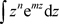 的原函数公式;在极点阶数的判断问题中补充了幂级数
的原函数公式;在极点阶数的判断问题中补充了幂级数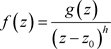 ,
, 情形,推广实变函数中的洛必达法则,并给出了相关证明。
情形,推广实变函数中的洛必达法则,并给出了相关证明。
基金项目
海南大学教育教学
改革研究课题“大学数学教与学的趣味性探究”(hdjy1853);海南大学本科双语课程建设项目《高等数学III》(hdsyk201903);“大学数学MOOC与翻转课堂相结合的教学研究”(海南大学hdjy1819,海南省高等学校教育教学改革研究项目Hnjg 2018-4);国家自然科学基金“k-耦合非线性薛定谔系统的未决问题”(11601109)。
文章引用
徐 瑞,岳晓蕊. 复变函数教学中的几个注释
Several Notes in the Teaching of Complex Functions[J]. 理论数学, 2019, 09(10): 1167-1173. https://doi.org/10.12677/PM.2019.910143
参考文献
- 1. 滕兴虎, 滕加俊, 周华任, 吴红. 关于2个幂级数和的收敛半径问题[J]. 高师理科学刊, 2008(28): 86-87.
- 2. 杨继明. 缺项幂级数收敛域的求法[J]. 湖南工程学院学报, 2009(19): 50-51.
- 3. 王刚, 战学秋, 田秋野. 有关幂级数收敛域的问题[J]. 吉林化工学院学报, 1998(15): 71-73.
- 4. 张建元, 张毅敏, 熊绍武. K-解析函数的双边幂级数与孤立奇点[J]. 云南民族大学学报, 2009(18): 198-201.
- 5. 马娜蕊. 幂级数收敛半径的一些求法[J]. 高等数学研究, 2004(7): 37-38.
- 6. 郝志峰. 复变函数与积分变换[M]. 上海: 复旦大学出版社, 2015.
- 7. 马凤丽, 杨素娟. 极点级数的判定办法[J]. 高师理科学刊, 2012(32): 23-25.
NOTES
*通讯作者。








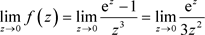 ,由定理5得
,由定理5得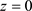 是
是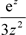 的2级极点,因此
的2级极点,因此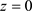 是
是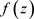 的2级极点。
的2级极点。 复幂级数的收敛半径以及可变量代换求解幂级数的收敛域这两类问题;在求解指数函数原函数的问题中总结了
复幂级数的收敛半径以及可变量代换求解幂级数的收敛域这两类问题;在求解指数函数原函数的问题中总结了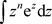 与
与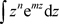 的原函数公式;在极点阶数的判断问题中补充了幂级数
的原函数公式;在极点阶数的判断问题中补充了幂级数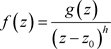 ,
, 情形,推广实变函数中的洛必达法则,并给出了相关证明。
情形,推广实变函数中的洛必达法则,并给出了相关证明。