Pure Mathematics
Vol.
10
No.
04
(
2020
), Article ID:
35023
,
9
pages
10.12677/PM.2020.104038
Asymptotic Solutions and Eigenvalues of a Class of Discontinuous Dirac Operators
Xing Gao
School of Mathematics and Information Science, Shaanxi Normal University, Xi’an Shaanxi

Received: Mar. 20th, 2020; accepted: Apr. 7th, 2020; published: Apr. 14th, 2020

ABSTRACT
In this paper, we study the asymptotics of the solutions and eigenvalues of Dirac operators defined on with jump conditions at point . The asymptotics of the solutions and eigenvalues were obtained, and the results to the case of n jump points were extended.
Keywords:Dirac Operator, Solution, Eigenvalue, Asymptotics

一类非连续Dirac算子解和特征值的渐近式
高星
陕西师范大学,数学与信息科学学院,陕西 西安

收稿日期:2020年3月20日;录用日期:2020年4月7日;发布日期:2020年4月14日

摘 要
本文研究定义在 区间上,在点 具有跳跃条件的Dirac算子解和特征值的渐近性,给出了解和特征值的渐近式,并将所得结论拓展到n个跳跃点的情形。
关键词 :Dirac算子,解,特征值,渐近式

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 预备知识
考虑定义在 上的Dirac微分方程:
(1)
满足边界条件
(2)
(3)
和跳跃条件
(4)
其中 , 为实值连续函数, ,,。
Dirac算子又称AKNS算子,具有跳跃(或不连续,传递)条件的非连续Dirac边值问题在数学物理、力学、电子学、地球物理学和其他自然科学的分支中具有广泛应用,如地壳底部横波的反射可能使描述原系统的物理方程中的特征函数具有跳跃点。在Dirac算子谱理论的研究中,解和特征值的渐近估计是基本问题。文献 [1] 利用留数方法给出了Dirac算子的谱分解;文献 [2] 根据积分方程的方法讨论了Dirac算子特征值的渐近式;文献 [3] 借助Prüfer变换给出了Dirac问题的特征值渐近估计式。文献 [4] 利用摄动的方法研究了非连续Sturm-Liouville算子特征值的渐近式。文献 [5] [6] [7] [8] 研究了Dirac算子特征值的性质。
本文将利用Dirac方程解的基本性质计算问题(1)~(4)解的渐近式,借助文献 [4] 中摄动的方法,利用
时具有跳跃条件的Dirac算子的特征值 刻画问题(1)~(4)的特征值。并将所得结论推广至
原系统具有n个跳跃点的情形。
2. 主要结论
令 和 的分量 分别是 和 上的连续可微函数。记 。若 和 满足跳跃条件(4),则
(5)
即函数 在 上连续。若 和 分别为方程 和 的解,则
(6)
令 ,,, 是方程(1)的解,满足跳跃条件(4)和如下初始条件
(7)
(8)
(9)
(10)
则 。
令 和 是方程(1)的解,满足初始条件:
(11)
但不满足跳跃条件。令
(12)
由文献 [2] 可知, 的取值与x无关,函数 为算子 的特征值函数。则
(13)
其零点为算子 的特征值,记为 ,。
引理1 [1] (1) 为算子 的特征函数,且
(14)
(2) 记
(15)
为特征值 对应的规范常数,且
(16)
其中 。
(3) 特征值 是实数,特征函数 和 为实值函数, 的零点是简单的,即 。在 空间中,不同特征值对应的特征函数是正交的。
根据跳跃条件(4)可得当 时,有
 (17)
(17)
当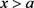 时,有
时,有
 (18)
(18)
其中
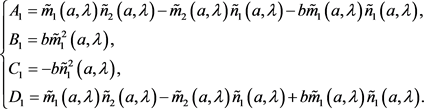 (19)
(19)
由文献 [2] 可知,函数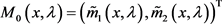 和
和 满足下列积分方程:
满足下列积分方程:
 (20)
(20)
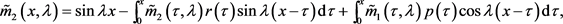 (21)
(21)
 (22)
(22)
 (23)
(23)
当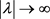 时,
时,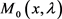 和
和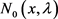 的渐近式如下:
的渐近式如下:
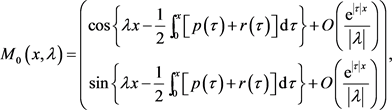 (24)
(24)
 (25)
(25)
其中 ,且
,且 。由(20)~(23)可得
。由(20)~(23)可得
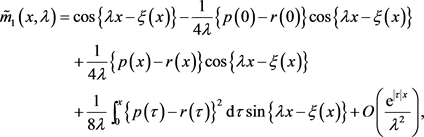 (26)
(26)
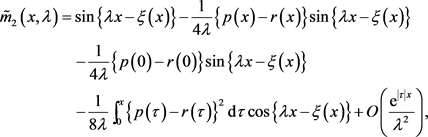 (27)
(27)
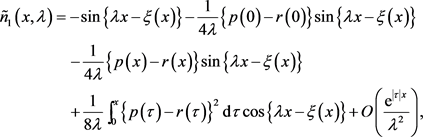 (28)
(28)
 (29)
(29)
其中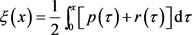 。由(19)和(26)~(29)可得
。由(19)和(26)~(29)可得
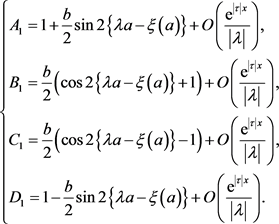 (30)
(30)
因为
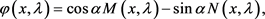 (31)
(31)
故通过(17)~(18)和(26)~(30)计算可得
 (32)
(32)
 (33)
(33)
Dirac算子(1)~(4)的特征值函数为
 (34)
(34)
由(32)~(34)可得
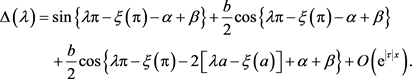 (35)
(35)
下面求特征值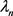 的渐近式。令
的渐近式。令 是函数
是函数
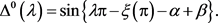 (36)
(36)
的零点。则
 (37)
(37)
此处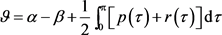 。Dirac算子(1)~(4)的特征值具有如下的渐近形式:
。Dirac算子(1)~(4)的特征值具有如下的渐近形式:
 (38)
(38)
将(32)和(33)代入规范常数(15)可得
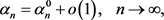 (39)
(39)
此处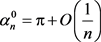 ,即
,即 。由(16)可得
。由(16)可得
 (40)
(40)
即 等价于常数
等价于常数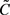 。
。
下面计算特征值更为精确的渐近式。令(35)式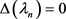 ,可得
,可得
 (41)
(41)
根据(38)式可得
 (42)
(42)
因为
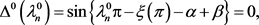 (43)
(43)
故由(41)可得
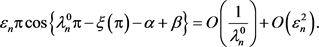 (44)
(44)
由(36)可得
 (45)
(45)
因此
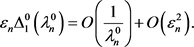 (46)
(46)
由(40)可得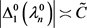 ,故
,故
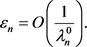 (47)
(47)
将(35)代入 ,根据(47)可得
,根据(47)可得
 (48)
(48)
其中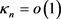 ,且
,且
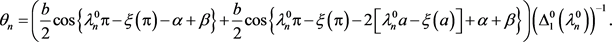 (49)
(49)
3. 具有n个跳跃点的Dirac方程
考虑问题(1)~(3),将(4)的跳跃点增至有限多个, ,即满足跳跃条件
,即满足跳跃条件
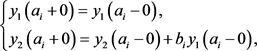 (50)
(50)
其中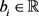 。
。
令 ,
,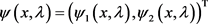 ,
,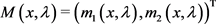 ,
,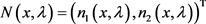 是方程(1)满足初始条件
是方程(1)满足初始条件
 (51)
(51)
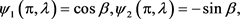 (52)
(52)
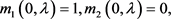 (53)
(53)
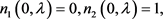 (54)
(54)
和跳跃条件(50)的解。
令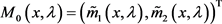 和
和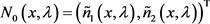 是方程(1)的解,即不满足跳跃条
是方程(1)的解,即不满足跳跃条
件,满足如下初始条件:
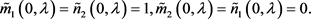 (55)
(55)
根据跳跃条件(50)可得
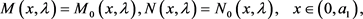 (56)
(56)

 (57)
(57)

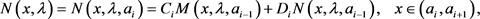 (58)
(58)

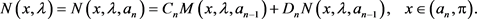 (59)
(59)
在(58)和(59)中, ,且(59)式可表示如下:
,且(59)式可表示如下:
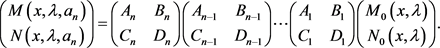 (60)
(60)
定义函数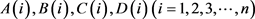 为
为
 (61)
(61)
由跳跃条件(50)计算可知, ,当
,当 时:
时:
 (62)
(62)
当 时,则有
时,则有
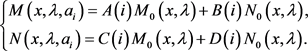 (63)
(63)
由(26)~(29)和(61)可得
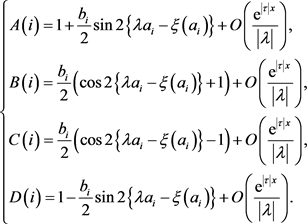 (64)
(64)
因为
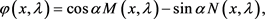 (65)
(65)
故由(56)~(61)和(64)计算可得
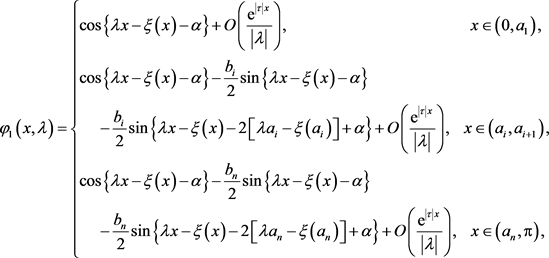 (66)
(66)
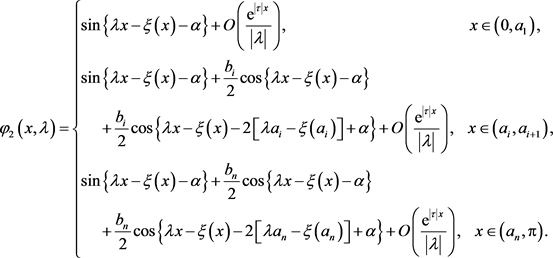 (67)
(67)
Dirac算子(1)~(3)和(50)的特征值函数为
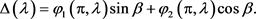 (68)
(68)
由(66)~(68)可得
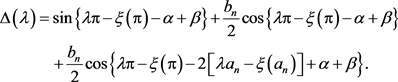 (69)
(69)
具有n个跳跃点的Dirac方程特征值渐近式的求法与第二部分相似,计算可得
 (70)
(70)
其中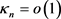 ,且
,且
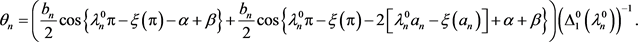 (71)
(71)
文章引用
高 星. 一类非连续Dirac算子解和特征值的渐近式
Asymptotic Solutions and Eigenvalues of a Class of Discontinuous Dirac Operators[J]. 理论数学, 2020, 10(04): 298-306. https://doi.org/10.12677/PM.2020.104038
参考文献
- 1. 朱俊逸. 常型Dirac算子的谱分解[J]. 郑州大学学报: 理学版, 2003, 35(1): 11-15.
- 2. Levitan, B.M. and Sargsjan, I.S. (1991) Sturm-Liouville and Dirac Operator. Kluwer Academic Publishers, Dordrecht, 185-212. https://doi.org/10.1007/978-94-011-3748-5
- 3. 郝萍萍, 魏广生. 一类Dirac算子特征值的渐近式[J]. 山东大学学报:理学版, 2015, 50(2): 55-59.
- 4. Freiling, G. and Yurko, V. (2001) Inverse Sturm-Liouville Problems and Their Applications. Nova Science Publishers, Huntington, NY.
- 5. 魏朝颖, 魏广生. 非连续Dirac算子谱的分布及其逆谱问题[J]. 应用数学学报, 2014, 37(1): 170-177.
- 6. Ozkan, A.S. and Amirov, R.Kh. (2011) An Interior Inverse Problem for the Impulsive Dirac Operator. Tamkang Journal of Mathematics, 42, 259-263. https://doi.org/10.5556/j.tkjm.42.2011.824
- 7. Horváth, M. (2001) On the Inverse Spectral Theory of Schr?dinger and Dirac Operators. American Mathematical Society Translations, 353, 4155-4171. https://doi.org/10.1090/S0002-9947-01-02765-9
- 8. 曹之江. 常微分算子[M]. 上海: 上海科技出版社, 1986: 65-85.