Pure Mathematics
Vol.
10
No.
09
(
2020
), Article ID:
37735
,
10
pages
10.12677/PM.2020.109099
t分布的渐进正态性证明及其特点分析
杨欣童
东北大学秦皇岛分校数学与统计学院,河北 秦皇岛

收稿日期:2020年8月24日;录用日期:2020年9月15日;发布日期:2020年9月22日

摘要
前人的研究已经证明t分布函数具有渐进正态的特性。我们改进了前人的研究,应用差函数的特性再次证明了t分布的渐进正态性,并结合MATLAB,直观验证了t分布的这一特性。之后,我们借助直观图形进一步分析了t函数的特性。
关键词
t分布,正态性,证明,MATLAB
Proof of Asymptotic Normality of t Distribution and Analysis of Its Characteristics
Xintong Yang
School of Mathematics and Statistics, Northeastern University at Qinhuangdao, Qinhuangdao Hebei

Received: Aug. 24th, 2020; accepted: Sep. 15th, 2020; published: Sep. 22nd, 2020

ABSTRACT
Previous studies have proved that the t distribution function has the characteristics of asymptotic normality. This paper applies the characteristics of the difference function to prove the asymptotic normality of the t distribution again, improving the previous research. And with the use of MATLAB software, the asymptotic normality is verified intuitively. After that, we further analyze the characteristics of the t function with the help of intuitive graphics.
Keywords:t Distribution, Normality, Proof, MATLAB

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在概率统计学中,t分布函数是一种十分重要的分布函数,这种分布函数具有渐进正态性,即当自由度n趋于无穷大时,t分布函数趋近于标准正态分布。前人已经用求极限的方法证明了此结论 [1] - [9],但是证明过程比较复杂,并且前人没有给出这个过程的细致描述。因此,对于这个逼近过程具有什么样的具体特点不是很清楚。本文拟引进t分布函数与标准正态分布的差函数,首先分析差函数的性质,利用差函数的性质简明地证明t分布的极限分布为标准正态分布,然后,通过利用MATLAB绘制其函数图像来细致分析其逼近过程的具体特点。
2. t分布及其性质
2.1. t分布的定义
若两个独立的随机变量 ,,那么随机变量 服从自由度为n的t分布 [10]。
其概率密度函数为
, (1)
2.2. t分布的性质
性质1 (t分布的等价定义):若 个独立的随机变量 ,
,那么随机变量 ,服从自由度为n的t分布;
性质2 (对称性):由t分布的概率密度函数可得 成立,因此t分布的概率密度函数关于x轴对称;
性质3 (均值和方差):若随机变量 ,则X的方差与均值为 , ;
性质4 (有界性):若随机变量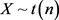 ,因为
,所以当
时X的方差有界,因此X的概率密度函数有界。
,因为
,所以当
时X的方差有界,因此X的概率密度函数有界。
3. 利用差函数分析证明渐进正态性
t分布函数与标准正态分布的差函数的意义为两者在y轴方向的距离,若当n趋于无穷时,差函数在其各极值点的取值均趋于0,则可间接证明当n趋于无穷时,t分布趋于标准正态分布,即
若 ,则 趋近标准正态分布 。
因此,下面首先分析差函数的性质,再利用差函数的性质证明t分布的极限分布为标准正态分布。
3.1. 差函数的定义
设随机变量的取值为x,则有标准正态分布的概率密度函数为 ,自由度为n的t分
布的概率密度函数为
(2)
这样,自由度为n的t分布与标准正态分布的差函数表达式为:
(3)
3.2. 差函数的基本性质
性质1 (对称性):已知标准正态分布和t分布的概率密度函数均关于x轴对称,因此差函数也关于x轴对称;
性质2 (极值点):对 关于x求导数,得到
(4)
令 得到极值点 ,另有极值点 满足方程
(5)
利用上式方程得到差函数的极值
(6)
3.3. t分布的正态渐进性证明
引理1 (瓦里斯公式推论):
(7)
证明:
已知瓦里斯公式为
(8)
公式左端变形后为
(9)
再次变形得到
(10)
证毕
定理1:当 时,差函数的极值均趋于0。
证明:
首先,带入极值点 得到
(11)
当n为偶数时,不妨令
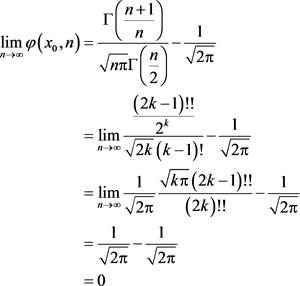 (12)
(12)
当n为奇数时同理可证明 。
下面,考虑其他极值点的极值
 (13)
(13)
又由于t分布的概率密度函数的有界性得到
, (p为一有限数) (14)
另外因为
(15)
所以
(16)
综上,当 时,差函数的极值趋于0。
因此,t分布的极限分布为标准正态分布。
4. t分布函数的渐进正态性直观验证
前文已经证明了t分布函数具有渐进正态性,但没有给出直观描述。下面首先利用MATLAB对其渐进正态性进行分析。在MATLAB中,输入下列代码,绘制标准正态分布以及自由度从1到100的t分布的概率密度函数。
clear all;clc;
x=-4:0.1:4;
n=linspace(1,100,100);
axis([-4 4 0 0.41]);
ylabel('$t(n)$','interpreter','latex', 'FontSize', 18);
xlabel('x')
for i=1:100
A(i,:)=tpdf(x,n(i));
end
plot(x,A);
hold on;
z=normpdf(x,0,1)
plot(x,z,'color','r','linewidth',2.3);
title('自由度从1到100的t分布密度函数和标准正态分布');
legend('n从1变化到100');
结果如图1所示。有图1可知,当t分布函数的自由度n增大的时,其概率分布函数在0附近的部分上升,其余两边的部分下降,总体趋近于标准正态分布曲线。t分布函数确实具有渐进正态性。
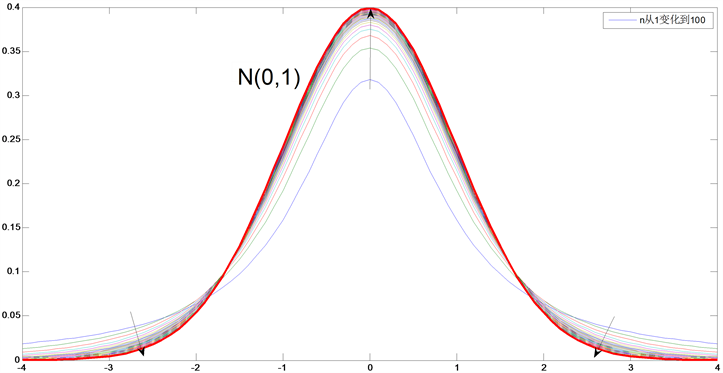
Figure 1. Asymptotic normality of t distribution
图1. t分布的渐进正态性
5. 利用差函数分析其具体特点
5.1. 差函数的变化图像
输入如下代码,绘制此函数当参数n 从1变化到100的函数图像。
clc;clear all;
x=-4:0.01:4;
n=linspace(1,100);
axis([-4 4 -0.2 0.41]);
ylabel('$t(n)-N(0,1)$','interpreter','latex', 'FontSize', 18);
xlabel('x')
z=normpdf(x,0,1)
for i=1:100
A(i,:)=tpdf(x,n(i))-z;
end
plot(x,A);
title('自由度从1到100的t分布密度函数与标准正态分布的差函数');
legend('n从1变化到100');
结果如图2所示。从图2中可以看出,当参数n固定时,差函数是一个关于y轴对称的函数,这表明标准正态分布和t分布都是关于y轴对称的函数。
另外,当参数n固定时,很容易看出,一条差函数曲线具有5个极值点。由于其对称性,其中一个极值点为 ,但它不是最值点。因此,虽然t分布和标准正态分布的最大值点都在 处取得,但是他们的差的最大值并不是在 处取得,而是在其他的极值点处取得。
当参数n从1增加到100时,差函数图像逐渐趋于x轴,整体变得平阔,函数范围越来越小,这直观地反映了当n增加时,t分布逐渐趋近于标准正态分布。
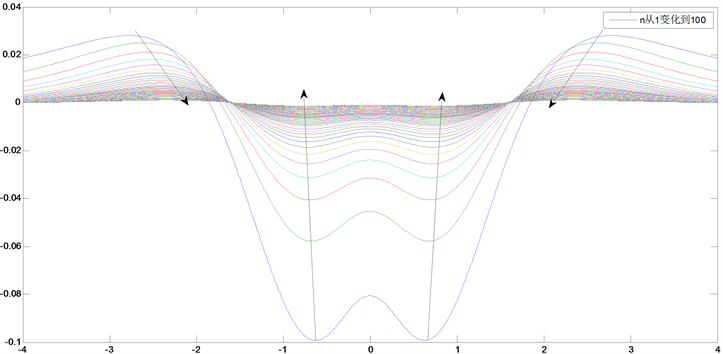
Figure 2. The image of difference function
图2. 差函数的变化图像
5.2. 差函数的最值
为了进一步分析差函数的性质,输入如下代码,求其当参数n从1变化到100时的差函数的最值。
clc;clear all;
MAX=[];MIN=[];a=zeros(1,5)
x=-4:0.01:4;
n=linspace(1,100);
axis([-4 4 -0.2 0.41]);
z=normpdf(x,0,1)
for i=1:100
A(i,:)=tpdf(x,n(i))-z;
MAX(i)=max(A(i,:));
MIN(i)=min(A(i,:));
end
ma=vpa(MAX,3);
ma1=[ma a]
ma2=reshape(ma1,7,[])
ma3=vpa(ma2.',4)
mi=vpa(MIN,5)
mi1=[mi a]
mi2=reshape(mi1,7,[])
mi3=vpa(mi2.',3)
结果为:
从表1、表2所得数据可以看出,当差函数的参数从1变化到100时,差函数最大值从0.028099变化到0.001139,最小值从−0.099264变化到−0.0013572,显然,他们的绝对值都减小了很多。
Table 1. The maximum of difference functions
表1. 差函数最大值
Table 2. The minimum of difference functions
表2. 差函数最小值
5.3. 差函数最值的直观表示
为了使差函数最值随n的变化更直观,输入如下代码,绘制其当n从1变化到100函数的图像。
clc;clear all;
syms E F;
X1=[];X2=[];SUP=[];INF=[];
x=-4:0.001:4;
n=linspace(1,100);
z=normpdf(x,0,1)
for i=1:100
A(i,:)=tpdf(x,n(i))-z;
SUP(i)=max(A(i,:));
INF(i)=min(A(i,:));
E=find(A(i,:)==SUP(i))
X1(i)=(E(:,2)-4000)*0.01
F=find(A(i,:)==INF(i))
X2(i)=(F(:,2)-4000)*0.01
end
plot(n,SUP,'o-','color','r','linewidth',2);
hold on;
plot(n,INF,'s-','color','b','linewidth',2);
title('参数从1到100的的差函数最值');
legend('差函数最大值','差函数最小值');
ylabel('$t(n)-N(0,1)最值$','interpreter','latex', 'FontSize', 18);
xlabel('n')
grid on;
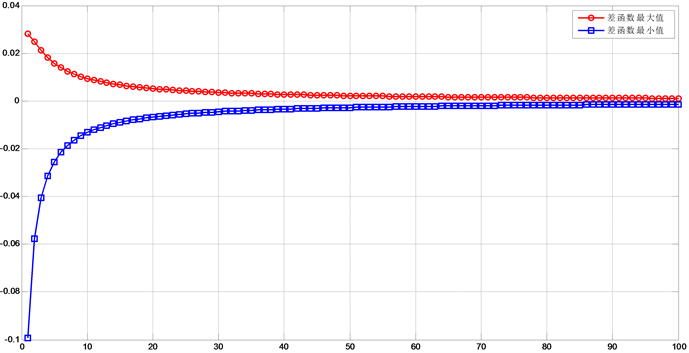
Figure 3. The maximum value of the difference function varies with n
图3. 差函数最值随n的变化
结果如图3所示。从图3可以看出差函数的最大值和最小值随参数n的增大都趋于0。当n增加时,函数的变化速度减慢,因此看出,自由度n增加时,t分布渐进于标准正态分布的速度减慢。
6. 结论
1) 当自由度n趋于无穷的时,t分布总体趋近于标准正态分布曲线,可通过构造的差函数比较简单地证明;
2) 趋近方式为其概率分布函数在0附近的部分上升,其余两边的部分下降;
3) 当自由度n趋于无穷的时,t分布趋近于标准正态分布,但是速度越来越慢;
4) 当自由度n趋于无穷的时,t分布在不同点与标准正态分布的差值不相同;
5) 当自由度n趋于无穷的时,t分布不同点趋近于标准正态分布的速度不相同。
文章引用
杨欣童. t分布的渐进正态性证明及其特点分析
Proof of Asymptotic Normality of t Distribution and Analysis of Its Characteristics[J]. 理论数学, 2020, 10(09): 852-861. https://doi.org/10.12677/PM.2020.109099
参考文献
- 1. 杨洁, 李兆庚. 关于t分布的极限分布为标准正态分布的证明[J]. 石油化工高等学校学报, 1994(3): 78-80.
- 2. 严琴, 唐贺, 李开灿. 中心多元t分布的一致渐近正态性[J]. 湖北文理学院学报, 2013, 34(2): 9-13.
- 3. 李开灿, 孟赵玲. x~2分布、t分布和F分布的一致渐近正态性[J]. 北京印刷学院学报, 2004(3): 30-33.
- 4. 梁琼. X~2•T•F分布的正态逼近[J]. 湖北民族学院学报(自然科学版), 1995(2): 33-38.
- 5. 王娟. t分布密度函数之性质[J]. 淮阴工学院学报, 2007(5): 15-21.
- 6. 彭定忠, 张映辉, 刘朝才. t分布概率密度的分析[J]. 湖南城市学院学报(自然科学版), 2012, 21(4): 50-52.
- 7. 张光远. 关于多元t分布的一些讨论[J]. 新疆大学学报(自然科学版), 1996(3): 33-38.
- 8. Li, R. and Saralees, N. (2020) A Review of Student’s t Distribution and Its Generalizations. Empirical Economics, 58, 1461-1490. https://doi.org/10.1007/s00181-018-1570-0
- 9. Chen, C.P. (2018) Complete As-ymptotic Expansions for the Density Function of t -Distribution. Statistics and Probability Letters, 141. https://doi.org/10.1016/j.spl.2018.05.014
- 10. 魏宗舒. 概率论与数理统计教程[M]. 北京: 高等教育出版社, 2008: 145-146.
