Computer Science and Application
Vol.08 No.04(2018), Article ID:24507,8
pages
10.12677/CSA.2018.84052
Kidney-Inspired Algorithm Based on Scaling Factor and Cooperative Operator
Qi Ke, Jiechang Wen
School of Applied Mathematics, Guangdong University of Technology, Guangzhou Guangdong

Received: Apr. 5th, 2018; accepted: Apr. 18th, 2018; published: Apr. 25th, 2018

ABSTRACT
In this paper, the kidney-inspired algorithm (KA) is studied in the optimization problem. It improves the defects in the kidney algorithm (KA) and shows good results in many optimization problems. For the KA algorithm, there is a problem that the search accuracy is low and it is easy to fall into the local optimum early on some functions. A cooperative operator was introduced to increase the diversity of the population and a scaling factor was added to the reabsorption update formula to achieve the goal of jumping out of the local optimal solution. Experimental comparison shows that the improved algorithm is an effective stable algorithm with higher accuracy and faster convergence speed.
Keywords:Optimization, Kidney-Inspired Algorithm, Cooperative Operator, Scaling Factor
基于缩放因子和协作算子的肾脏算法
柯琪,温洁嫦
广东工业大学应用数学学院,广东 广州

收稿日期:2018年4月5日;录用日期:2018年4月18日;发布日期:2018年4月25日

摘 要
本文研究优化问题中的肾脏算法(Kidney-inspired algorithm, KA) [1] ,对肾脏算法(KA)存在的缺陷进行了改进,并在许多优化问题中显示出不错的效果。针对KA算法在某些函数上寻优精度低、且容易过早地陷入局部最优的问题。引入了协作算子来增加种群多样性,并在重吸收更新公式上加入缩放因子,达到跳出局部最优解的目的。实验对比说明,改进的算法是一个有效的稳定算法,具有更高的求解精度和更快的收敛速度。
关键词 :最优化,KA算法,协作算子,缩放因子

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
肾脏算法是由Jaddi等人在2017年提出的一种基于肾启发式算法的优化算法,它的灵感来自于尿液在人体肾脏中的产生。在肾脏的过程中,尿的形成有四个步骤:过滤、重吸收、分泌、排泄。KA从初始种群开始,血液中包含水和溶质。在每一次迭代中,通过利用所有溶质的目标函数(MOF)的均值来控制种群中溶质的过滤。过滤后分为两部分,过滤后的血液(FB)和尿原液(W)。尿原液在移动中较优的溶质会被重吸收进入FB,否则从W中排泄出去;另一方面,重吸收进入FB的溶质不比FB中最差的溶质为好,则从FB中分泌出去。溶质即是目标函数的解。然后对所有的解进行排序,将FB和W中的解进行合并,并更新过滤率,进行下一次迭代。在此算法中,基于当前解和迄今为止发现的最优解,生成趋近当前最优解的新解,通过迭代寻找出全局最优解 [2] 。在算法被提出后,许多学者对肾脏算法的应用进行了研究。Wang, Haichao [3] 等人将KA算法应用到主动配电系统规划。Liang, Yi [4] 等人将KA算法与BP神经网络结合用来评估预测碳排放。
在所有的优化算法中,主要的目标是找到全局最优 [5] 。要实现这一目标,就必须在寻优和增加种群多样性之间取得平衡 [6] 。在KA算法中,溶质的运动和过滤过程为算法提供了良好的寻优能力,另外重吸收过程为增加种群多样性提供了很好的条件 [7] 。然而重吸收更新公式可能使算法陷入局部最优,为了提高寻优和增加种群多样性之间的平衡,本文在重吸收更新公式上加入缩放因子 [8] ,避免重吸收后的解聚集在局部最优解的附近,扩大寻优范围。并引入协作算子 [9] ,通过种群间个体的信息互换,增加种群多样性 [10] 。
本文组织结构如下:第2章介绍KA算法;第3章详细讨论重吸收更新公式缩放因子和协作算子的插入以及改进的算法;第4章为实验设置和结果分析;第5章总结。
2. KA算法
在KA算法的初始阶段,创建一个随机的种群,并计算它们的目标函数值。然后,通过应用过滤算择较优个体移动到FB (Filtered Blood),其他稍差一点的个体进入W (Waste),算法中的FB表示较优个体的集合,W表示较差个体的集合。如果一个个体被分配给W,这个算法会给这个个体一次更新,使它有进入FB中的机会。如果更新后的个体质量较差,则从W中排泄出去然后随机加入一个个体。另一方面,如果一个个体分配给FB,但这个个体并不比FB中最差的个体要好,就从FB中分泌出去。最后对FB的个体进行排序,并更新最优解( )。对过滤速率进行更新,并合并FB和W,进行下一次迭代。
2.1. 虚拟溶质的运动
种群中的个体代表了生物血液中的溶质。在KA的初始化阶段,和其他的算法一样,生成一个随机种群,并计算每个个体的目标函数值。在每次迭代中,通过移动到当前最优的方向,为所有的个体创建一个新的个体。这一运动的制定如下:
(1)
s表示KA的一个解(或生物肾脏中的溶质)。 是第i次迭代中的个体。rand的值是介于0和给定数之间的随机数,而 是在过去的迭代中被算法发现的最优个体。
2.2. 过滤
种群中的个体是通过每次迭代中使用的过滤函数计算的过滤速率来过滤的。过滤速率 计算如下:
(2)
α的值是一个常数值的范围(0, 1),在算法开始时设定。p是种群的大小。 是第i代中求解的目标函数,在这个公式中可以看出,每次迭代的过滤速率依赖于种群中所有解的目标函数值。过滤速率以调节α来调整算法的收敛性。在每一次迭代中,目标函数的值越接近全局最优值,因此计算基于这些解的过滤速率,提高了FB中个体的质量。
2.3. 重吸收
重吸收算子是一个过程,它给被分配给W中的个体一次更新。将重吸收更新公式(式1)再次应用,如果它满足过滤要求,则可以将分配给W的个体转移到FB。这是对生物肾脏中溶质的再吸收的模拟。重新吸收过程增加了种群多样性,扩大寻优范围。
2.4. 分泌和排泄
如果分配给FB的个体不比FB中最差的个体好,那么它就会被转移到W,然后从W中删除(即模仿肾脏的排泄过程);否则,这个个体仍然在FB中,而FB中最差个体被转移到W。
算法步骤:
1) 初始化种群,用计算个体的目标函数值,将种群最优个体作为当前全局最优 。
2) 设置过滤率 ,。设置较差个体集W,较优个体集FB;设置迭代次数mumofite。
3) 个体进入过滤过程,如果该个体适应度值优于 ,则该个体没有过滤,进入FB;否则该个体过滤后进入W。
4) 如果一个个体过滤后进入W,通过重吸收算子更新。若更新后个体适应度值差于 ,则从W中移除,然后随机加入一个新个体代替;若更新后个体适应度值优于 ,则重吸收进入FB。但如果优于FB中的最差个体 ,则将 分泌到W;如果差于FB中的 ,也将重吸收到FB中的个体分泌入W。
5) 将FB中的个体排序,并更新 ;合并FB和W,更新过滤率,进行下一次迭代。
3. 基于缩放因子和协作算子的肾脏算法
针对标准KA算法在某些测试函数有可能陷入局部最优、寻优精度低及收敛速度慢等缺陷,本文对重吸收更新公式增加两个缩放因子并在一次迭代结束后更对FB部分引入协作算子 [11] 。协作算子通过个体间信息共享,既可增加种群多样性,也可优化个体;通过调节缩放因子 [12] 尽量避免较优个体全部聚集在局部最优附近,达到避免算法陷入局部最优的目的 [12] 。
3.1. 加入缩放因子的重吸收更新公式
传统肾脏算法重吸收过程的更新公式导致算法在有些测试函数中容易陷入局部最优,更新后的个体聚集在当前最优附近 [13] 。本文加入缩放因子 , 为非负数,控制前一个体对当前个体的影响, 调节个体移向当前最优的步长;通过调节 ,避免更新后的个体聚拢在当前最优附近,避免算法陷入局部最优。
(3)
其中 为当前代中适应度值最优的个体, 和 为缩放因子。
3.2. 协作算子
协作算子有算术交叉算子和两点交叉算子两种形式,由交叉概率 控制决定,如果满足 ,则执行算术交叉操作,否则执行两点交叉操作。协作算子通过个体间信息共享,既可维持种群多样性,也可优化个体。
3.2.1. 算术交叉操作
改进后的KA算法中,若FB中个体 执行算术交叉操作,则从FB中选择当前最优个体 ,按以下方式产生新个体:
, (4)
. (5)
其中 表示算术交叉因子, 分别表示产生的新个体,若新个体优于 ,则更新 。通过个体与其他的优质个体交叉交换信息产生了两个新的个体,可有效保持种群的多样性,有利于种群的进化。
3.2.2. 两点交叉算子
改进后的KA算法中,若FB中的个体执行两点交叉操作,则从FB中随机选择个体 ,随机产生二个交叉点位置a、b,将交叉点所夹的片段进行交换产生新个体:
(6)
(7)
其中 , 分别表示产生的新个体,若新个体优于 ,则更新 ,否则以小概率p保留新个体,一般 。该算子能提高算法的收敛速度,一定程度上又维持了种群多样性。
3.3. 改进后的算法步骤
1) 初始化种群,计算个体的目标函数值,将种群最优个体作为当前全局最优 。
2) 设置过滤率 ,设置较差个体集W,较优个体集 ;设置迭代次数mumofite。
3) 个体进入过滤过程,如果该个体适应度值优于 ,则该个体没有过滤,进入FB;否则该个体过滤后进入W。
4) 如果一个个体过滤后进入W,通过重吸收算子更新。若更新后个体适应度值差于
,则从W中移除,然后随机加入一个新个体代替;若更新后个体适应度值优于
,则重吸收进入FB。但如果优于FB中的最差个体
,则将 分泌到W;如果差于FB中的
,也将重吸收到FB中的个体分泌入W。
分泌到W;如果差于FB中的
,也将重吸收到FB中的个体分泌入W。
5) 将FB中的个体排序,执行协作算子,并更新 ;合并FB和W,更新过滤率,进行下一次迭代。
4. 实验设置和结果分析
为了比较分析改进KA算法的性能,本文将改进的KA算法记为为C-KA (Cooperative operator Kidney-inspired algorithm),和原始KA算法在选取的CE2013 [14] 和CEC2014 [15] 测试集中的8个测试函数上进行测试,F1(Sphere)、F2(Rosenbrock)、F3(Rastrigin)、F4(Griewangk)、F5(Bent Cigar)、F6(HGBat)、F7(Schwefel)、F8(Weierstrass),并对实验结果进行对比。测试函数如表1所示。
4.1. 实验设置
数值实验运用MATLAB编程,为了比较的有效性,两种算法采用相同的参数设置,种群规模为100,最大迭代次数为100,同一条件下独立运行50次。本文设置协作算子中交叉概率Pc = 0.6,算术交叉因子r = 0.8,缩放因子 , 。记录实验结果的最优值、最差值、均值和标准差,最优值表示算法寻优最好的结果,最差值表示算法寻优最差的结果,均值显示算法寻优的平均水平,反映算法的稳定性,标准差表反映算法寻优结果的离散程度,表示算法的稳定性。优化计算结果如表2所示。
Table 1. Text Function
表1. 测试函数
Table 2. Optimum results of F1-F8
表2. F1-F8优化计算结果
4.2. 实验结果比较分析
由表2可知,F1、F3、F4、F5、F6、F7、F8测试函数,改进后算法的最差值、最优值、均值、标准差均优于原始KA算法。对于F2,新算法求出函数最优解的精度比原算法高;相对于F1、F3、F4、F5,新算法的精度为10-21、0、0、10-20,说明新算法有较高的求解精度;与原算法比较,新算法的实验数据大部分标准差均最小,说明新算法的稳定性较高 [16] 。
测试函数的进化曲线图如图1~4所示。由图所示可以看出,新算法收敛速度和寻优精度大部分优于原算法。新算法在重吸收更新公式上引入缩放因子,通过调节缩放因子增加随机扰动,可避免FB中的个体聚拢在局部最优值附近,以避免算法陷入局部最优新算法加入的协作算子能够提高种群多样性与种群质量,加强了算法的全局搜索能力;新算法加入的协作算子通过种群间的信息交流能够提高种群多样性与种群质量,加强了算法的全局搜索能力,有利于加快算法收敛速度,提高算法精度,因而整体上优化了算法性能 [17] 。

Figure 1. Convergence curves of F1 and F2 functions
图1. F1和F2函数进化曲线

Figure 2. Convergence curves of F3 and F4 functions
图2. F3和F4函数进化曲线
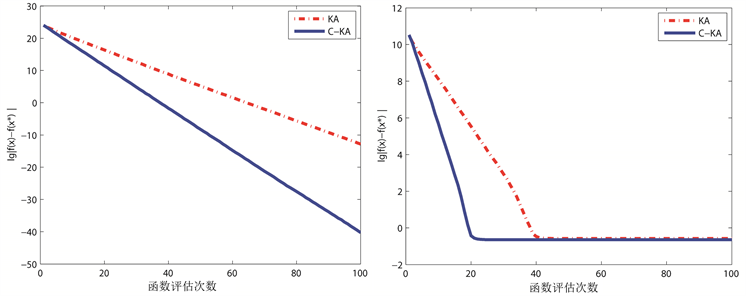
Figure 3. Convergence curves of F5 and F6 functions
图3. F5和F6函数进化曲线

Figure 4. Convergence curves of F7 and F8 functions
图4. F7和F8函数进化曲线
5. 结语
原KA算法对某些函数寻优精度低,容易过早的陷入局部最优解,本文提出一种加入协作算子和重吸收更新公式缩放因子的增强KA算法(C-KA)。通过在种群中执行协作算子,提高了种群多样性与种群质量;同时在重吸收更新公式上引入缩放因子,使种群的多样性增加且更有机会跳出局部最优区域,并在8个测试函数上进行仿真实验,与原始KA算法进行对比,表明新算法的寻优精度更高,收敛速度更快,算法更稳定。
致谢
感谢导师温洁嫦老师在写作期间给予我的指导和鼓励,感谢刘海林老师的指导!感谢同门的陪伴和关怀!
资助信息
广州市科技计划项目(502150155)。
文章引用
柯 琪,温洁嫦. 基于缩放因子和协作算子的肾脏算法
Kidney-Inspired Algorithm Based on Scaling Factor and Cooperative Operator[J]. 计算机科学与应用, 2018, 08(04): 472-479. https://doi.org/10.12677/CSA.2018.84052
参考文献
- 1. Jaddi, N.S., Alvankarian, J. and Abdullah, S. (2017) Kidney-Inspired Algorithm for Optimization Problems. Communi-cations in Nonlinear Science and Numerical Simulation, 42, 358-369. https://doi.org/10.1016/j.cnsns.2016.06.006
- 2. 马红伟. 粒子群算法改进及其在数据挖掘中的应用研究[D]: [硕士学位论文]. 济南: 山东师范大学, 2014.
- 3. Wang, H.C., Niu, D.X. and Chen, H.Y. (2017) Research on Coor-dination Planning of Micro Grid and Active Distribution Network Based on Kidney-Inspired Algorithm. Advances in Education Sciences, 12, 150-156.
- 4. Liang, Y., Niu, D.X. and Wang, H.C. (2017) Assessment Analysis and Fore-casting for Security Early Warning of Energy Consumption Carbon Emissions in Hebei Province, China. Energies, 10, 391. https://doi.org/10.3390/en10030391
- 5. 陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社, 2006.
- 6. 金希东. 遗传算法及其应用[D]: [硕士学位论文]. 成都: 西南交通大学, 1996.
- 7. 李士勇. 蚁群算法及其应用[M]. 哈尔滨工业大学出版社, 2004.
- 8. 郭鹏. 差分进化算法改进研究[D]: [博士学位论文]. 天津: 天津大学, 2011.
- 9. 徐焕芬, 刘伟, 谢月珊, 等. 双种群烟花算法[J]. 广东工业大学学报, 2017(5): 65-72.
- 10. 张创业, 莫愿斌. 基于协同进化思想的人工鱼和粒子群混合优化算法[J]. 广西民族大学学报: 自然科学版, 2009, 15(1): 74-77.
- 11. 慕彩红, 焦李成, 刘逸. M-精英协同进化数值优化算法[J]. 软件学报, 2009, 20(11): 2925-2938.
- 12. 慕彩红, 焦李成, 刘逸. 求解约束优化问题M-精英协同进化算法[J]. 西安电子科技大学学报(自然科学版), 2010, 37(5): 854-861.
- 13. 崔逊学. 多目标进化算法及其应用[M]. 北京: 国防工业出版社, 2006: 93-94.
- 14. Liang, J., Suganthan, P.N. and Hernandez-Diaz, A.G. (2016) Problem Definitions and Evaluation Criteria for the CEC2013 Special Session on Real-Parameter Optimization.
- 15. Liang, J.J., Qu, B.Y. and Suganthan, P.N. (2016) Problem Definitions and Evaluation Criteria for the CEC2014 Special Session and Competition on Single Objec-tive Real-Parameter Numerical Optimization. http://www.ntu.edu.sg/home/EPNSugan/index_files/CEC2014/CEC2014.htm
- 16. 李荣雨, 周志勇. 成长性的粒子群算法及其在函数优化中的应用[J]. 信息与控制, 2017, 46(2): 224-230.
- 17. 胡冠宇, 乔佩利. 混沌协方差矩阵自适应进化策略优化算法[J]. 吉林大学学报(工), 2017, 47(3): 937-943.
