Computer Science and Application
Vol.
09
No.
12
(
2019
), Article ID:
33291
,
7
pages
10.12677/CSA.2019.912250
Integer Programming Model and Algorithms for Dual-Objective Wireless Return Topology
Shaohu Wang, Yuhui Hu, Xuanhao Yang, Qu Gong
College of Automation, Chongqing University, Chongqing

Received: Nov. 14th, 2019; accepted: Nov. 29th, 2019; published: Dec. 5th, 2019

ABSTRACT
In the actual Relay deployment, the layout and connection of the sites are limited by various factors such as cost, distance, and backhaul quality, which bring challenges to the topology planning of the sites. Aiming at the problem of layout planning of communication base stations, a dual-objective station integer programming model is established, and a block partitioning algorithm based on K-means clustering algorithm and a site connection algorithm based on Prim algorithm are designed. The results of simulations show that the model and algorithms can effectively solve the problem of site planning in wireless backhaul topology, and it has better applicability and effectiveness while reducing the complexity of the algorithms.
Keywords:Wireless Backhaul Topology, Integer Programming, K-Means Clustering Algorithm, NP-Hard Problem
双目标无线回传拓扑整数规划模型及算法
王少虎,胡瑀晖,杨宣浩,龚劬
重庆大学数学实验教学中心,重庆

收稿日期:2019年11月14日;录用日期:2019年11月29日;发布日期:2019年12月5日

摘 要
在实际的Relay部署中,站点的布局及连接受成本、距离、回传质量等多种因素的限制,给站点的拓扑规划带来了挑战。针对通信基站的布局规划问题,建立了成本和路损最小的双目标整数规划模型,并基于K-means聚类算法和Prim算法设计了求解该NP难题的启发式算法。仿真结果表明,该模型和算法可以有效解决无线回传拓扑中的站点规划问题,在降低算法复杂度的同时具有较好的适用性和有效性。
关键词 :无线回传拓扑,整数规划,K-Means聚类算法,NP难题

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
基站的建设与布局一直是发展通信技术和提高网络覆盖率的重要环节 [1]。传统的光纤和微波传输方式由于建设费用高、传输条件高等限制因素,无法满足偏远地区的传输需求,且基站建设较为困难。Relay无线回传技术是目前兴起的新型传输技术,可以有效扩展网络覆盖范围 [2]。Relay系统主要包括宿主站(DeNB)和子站(RRN),宿主站通过子站将信号发送给用户 [3]。
在实际的Relay部署中,站点的布局及连接受成本、距离、回传质量等多种因素的限制,给站点的拓扑规划带来了挑战 [4]。
目前针对通信基站的布局规划问题已有一系列的研究:
石雷等 [5] 针对无线多跳网络的站点选址问题,提出了根据稀疏程度确定基站可行区域的方法,并设计了相关算法求解站点的具体位置;张宏远等 [6] 设计了基于聚类分解的分层算法求解大规模WCDMA无线网络基站布局规划问题;南雪莹 [7] 基于粒子群算法求得了成本最优的布站方案;张然 [8] 根据小区内基站的各项参数和信息特性,建立了0-1整数规划模型,并提出了一种混合遗传算法。Mark [9] 等提出了多种基站选址模型,包括覆盖模型等。Soto等 [10] 提出多页需求的移动网络基站选址算法,可以使成本大大降低。
基于上述研究,本文针对候选站点位置确定的情况,建立了一种考虑多种复杂约束条件的双目标大规模站点整数规划模型,由于该问题属于NP (Non-deterministic Polynomial)难题,本文综合聚类分析及图论的算法思想设计了启发式求解算法,最后给出了仿真结果。
2. 系统模型
本文研究的Relay站点部署规划问题为在确定候选站点位置的情况下,确定站点的类型及站点间的连接关系。其中,站点的类型包括宿主站(RuralStar和蝴蝶站)和子站。站点间的连接关系,包括宿主站与子站间的连接、子站间的连接关系及宿主站间的成片连接。
本文以站点站型和不同站点间连接关系为决策变量,成本与回传损耗为目标函数,在满足约束条件的情况下建立双目标规划模型。引入以下符号:
xi表示站点类型, 表示i站点为子站, 表示该站点为宿主站; 表示站点间的连接关系, 表示i与j站点没有连接关系, 表示站点间存在连接关系;e为宿主站的类型, 表示站型为RuralStar, 表示站型为蝴蝶站,RuralStar包含1个扇区,蝴蝶站包含2个扇区。 表示i与j站点间的距离:
(1)
其中 表示i站点的经纬度坐标,R为地球半径。
2.1. 规划目标
目标函数一:更低的总成本。
(2)
其中,P为总成本, 为宿主站的综合成本, 为子站的综合成本, 为卫星设备的成本,W为卫星的数量。
目标函数二:更低的回传路径损耗。任意两站i与j间的回传损耗 可以表示为:
(3)
其中F是发射频率。
则总回传损耗最小可以表示为:
。 (4)
2.2. 站点连接中的约束条件
1) 回传距离约束
在满足一定的回传质量情况下,站点间连接应满足(5)、(6)、(7)式
(5)
(6)
(7)
其中 表示宿主站与子站相连的距离门限, 和 分别为子站间、宿主站间相连的距离门限。
2) 站点间连接的拓扑约束 [11]
1˚站点包含RuralStar和蝴蝶站两种不同站型;其中,RuralStar共包含1个扇区,蝴蝶站共包含2个扇区 [12] ;若该站点为宿主站,则每个扇区第一级子站数目和子站总个数存在限制。表示如下:
(8)
(9)
其中, 为一级子站的数量门限, 为一个扇区内子站总个数的门限, 为第k个宿主站及其分配的子站构成的集合。
2˚每个子站最多只能有2条无线回传连接:
。 (10)
3) 宿主站间成片连接约束
任意宿主站都有且只有一颗卫星负责回传,成片连接的宿主站可共享同一颗卫星,但一颗卫星负责的宿主站个数存在限制,设成片连接的宿主站构成集合 ,则 内宿主站共用卫星数 应满足:
(11)
其中, 为一颗卫星负责的宿主站个数门限。
综上可构建问题的模型:
。
3. 求解算法
由于大规模站点的规划问题为NP难题,求精确最优解的算法都是指数时间的,本文基于聚类算法和最小生成树算法设计了求近似最优解的有效算法 [13] [14]。
对站点的坐标数据进行预处理之后,首先利用K-means聚类算法将大规模的候选站点位置划分为多个一级区块,在一级区块中以每个候选位置为宿主站,每次选取一个站点作为宿主站,利用最小生成树算法求解出多个连接方案。接着再次利用聚类算法将一级区块集划分为多个二级区块,每个二级区块内包含多种宿主站选择方案,设计Prim算法的启发式算法求解出二级区块内宿主站成片连接方案的可行解,最后建立宿主站选取模型,求解费用及损耗最低的方案。
站点聚类数为:
(12)
其中N为候选站点个数,每个区块的最大站点数目 。
聚类中心经纬度坐标为 ,其中:
(13)
基于K-means聚类算法和Prim算法的站点规划算法步骤为:
Step 1 利用K-means聚类算法将N个站点划分为M个区块: 。
Step 2 对每个区块求出最短的可行连接方案。
Step 2.1 令i = 1;
Step 2.2 在Di中任取一个站点作为宿主站,记为v0。令 ,,j = 0;
Step 2.3 若 ,则转Step 2.6,否则从V中找到与U中v0所关联的距离最小的边,若该边小于 ,则将该边加入Ei,将其关联的站点v1加入到U中, ,令 ,转Step 2.4;否则转Step 2.6。
Step 2.4 从V找与U中v1所关联的距离最小的边,若该边小于 ,则将该边加入Ei,将关联的站
点v2加入到U中, ,转Step 2.5,否则返回Step 2.3;
Step 2.5 从V开始找与U中v2所关联的距离最小的边,若该边小于 ,则将该边加入Ei,将关联的站点v3加入到U中,并且从V中删除,否则返回Step 2.3;
Step 2.6在区块中另设一个宿主站,记为v0,重复Step 2.2至Step 2.5,直到区块中所有站点遍历为宿主站,得到区块 所有可行连接方案,记为 。其中, 表示区块 内以i站点作为宿主站得到的连接方案。 ,若i < M,返回Step 2.1,否则,下一步。
Step 3 宿主站确定。
Step 3.1 K-means聚类分析确定二级区块:将一级区块中心点聚类为 个区块中心点的二级区块 ,以保证尽可能多的宿主站共用同一颗卫星;
Step 3.2 利用Prim算法确定二级区块中宿主站间的成片连接关系,之后判断每条边的长度是否小于 ,若成立,则保留,否则将该条边打断。得到二级区块 中任意一级区块宿主站可行方案组合下的卫星数量:
以及回传损耗:
Step 3.3双目标规划模型求解确定宿主站。基于Step 3.1和Step 3.2的结果,建立宿主站双目标规划模型确定宿主站的位置,针对每一个二级区块,卫星数量越少则总费用越小,同时需要使得回传损耗尽可能最小。模型如下:
s.t.
。
4. 仿真结果及分析
本节将采用随机模拟的仿真方法对本文的算法进行验证和评估 [15]。仿真场景选取为一个正方形区域。根据实际的情况设置系统仿真参数如表1所示。
Table 1. System simulation parameters
表1. 系统仿真参数表
使用matlab编程,随机产生1000个经纬度坐标,参考深圳市的地理坐标,经度范围控制在114.12˚至116.82˚,纬度范围控制在22.65˚至25.35˚;站型设为Ruralstar。

Figure 1. Final station plan diagram
图1. 最终部站方案图
求解出所有候选站点的部站方案如图1所示。在图1中,不同颜色的“*”表示该站点为不同一级区块的子站,红色“•”代表该站为宿主站。蓝色的“——”表示子站与子站或子站与宿主站之间通过无线回传连接,红色“——”表示宿主站与宿主站之间通过微波连接且共用一颗卫星。
1000个候选站点的规划方案为:宿主站共143个,卫星共18个,连接关系如图1所示。输出结果中,94.5%的站点都纳入规划,说明了算法具有很高的可靠性。算法输出结果的总成本为6660 WUSD,总的回传损耗为88,220。
保持站点数量不变,改变站点分布区域的面积,站点连接覆盖率的变化如图所示,平均回传损耗及费用的变化如图2所示。
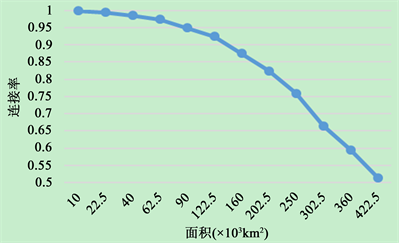
Figure 2. Site distribution area and site connection rate curve
图2. 站点分布区域面积与站点连接率曲线
图2和图3分别为站点分布区域面积变化时,规划覆盖率、总成本和回传损耗的变化曲线。图中可以看出,当区域面积小于9 × 104 km2时,算法可以保证95%以上的站点被规划到,且费用较低。当面积不断增大时,由于距离的增加,覆盖率逐渐减小,费用和平均回传损耗均不断增大。当区域面积大于2 × 105 km2时,即站点分布密度小于0.005个/km2,覆盖率减小的速率、费用和平均回传损耗增加的速率均明显增大。
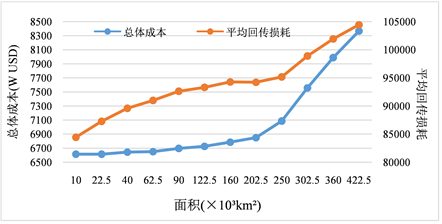
Figure 3. Site distribution area and overall cost/return loss curve
图3. 站点分布区域面积与总体成本/回传损耗曲线
5. 结论
本文研究了大规模站点情况下的无线回传拓扑规划问题,综合考虑站点连接中的条件限制,建立了双目标站点规划模型,由于这种问题属于NP难题,本文设计了基于K-means算法和Prim算法的启发式算法,可以有效解决无线回传拓扑规划中的站点规划问题。仿真结果表明,本文提出的算法具有较好的适用性和有效性。
文章引用
王少虎,胡瑀晖,杨宣浩,龚 劬. 双目标无线回传拓扑整数规划模型及算法
Integer Programming Model and Algorithms for Dual-Objective Wireless Return Topology[J]. 计算机科学与应用, 2019, 09(12): 2249-2255. https://doi.org/10.12677/CSA.2019.912250
参考文献
- 1. 詹子群. 关于通信运营商无线基站建设设计方面的探讨[J]. 电子测试, 2019(6): 64-65.
- 2. 董江波, 程伟, 陈燕雷, 韩云波. Relay技术引入对无线网络规划的思考与研究[J]. 电信工程技术与标准化, 2013, 26(7): 23-28.
- 3. 石朗昱, 马玲. Relay无线回传技术在TD-LTE组网方案中的应用研究[J]. 电信工程技术与标准化, 2017, 30(2): 41-43.
- 4. 张青松. 基站站址规划在通信基础设施城乡规划中的应用[J]. 通信电源技术, 2018, 35(10): 210-213.
- 5. 石雷, 刘正丽, 韩江洪, 石怡, 魏振春. 基于干扰管理的高吞吐无线多跳网络基站选址算法[J]. 电子测量与仪器学报, 2016, 30(3): 389-399.
- 6. 张宏远, 谷寒雨, 席裕庚. 基于聚类分解的WCDMA基站布局规划算法[J]. 控制与决策, 2006, 21(2): 213-216.
- 7. 南雪莹. 基于粒子群算法的Relay无线回传方案部站优化[J]. 中国新通信, 2019, 21(3): 128.
- 8. 张然. 移动回传网络的可靠性部署研究[D]: [硕士学位论文]. 北京: 北京邮电大学, 2016.
- 9. Dinwoodie, J. (1996) Network and Discrete Location: Models, Algorithms and Applications. Journal of Transport Geography, 4, 302-303. https://doi.org/10.1016/S0966-6923(97)89394-5
- 10. Lee, S., Lee, S.K., Kim, K. and Kim, Y.H. (2015) Base Station Placement Algorithm for Large-Scale LTE Heterogeneous Networks. PLoS ONE, 10, e0143265. https://doi.org/10.1371/journal.pone.0139190
- 11. Monti, P., Tombaz, S., Wosinska, L. and Zander, J. (2012) Mobile Backhaul in Heterogeneous Network Deployments: Technology Options and Power Con-sumption. 2012 14th International Conference on Transparent Optical Networks, Coventry, UK, 2-5 July 2012, 1-7. https://doi.org/10.1109/ICTON.2012.6253839
- 12. 马梁龑. 无线Relay传输技术在微基站部署中的策略[J]. 移动通信, 2017, 41(24): 13-18.
- 13. 章永来, 周耀鉴. 聚类算法综述[J/OL]. 计算机应用: 1-14.
- 14. 李建军, 沈啸林, 陈明贺, 刘硕, 陈舒研. 基于最小生成树算法的怀柔区快递站点选址问题研究[J]. 南方农机, 2019, 50(1): 91-93.
- 15. 曾宪昌. 求解智能问题的模拟仿真法[J]. 数学物理学报, 1983(4): 385-394.
