设为首页 加入收藏 期刊导航 网站地图

Mechanical Engineering and Technology
Vol.06 No.02(2017), Article ID:20946,7 pages
10.12677/MET.2017.62019

Recognition of Structural Damping Coefficient of Thin Plate Based on the Frequency Response Matrix Method

Quanjun Zhu1, Xiying Fan2, Meigen Cao3, Qingpeng Han4, Jianxing Ren4, Tiancheng Li4

1Global energy Interconnection Research Institute, Beijing

2Research Institute of Economics and Technology, State Grid Shanxi Electric Power Company, Taiyuan Shanxi

3China electric power research Institute, Beijing

4College of Energy and Mechanical Engineering, Shanghai University of Electric Power, Shanghai

Received: May 25th, 2017; accepted: Jun. 7th, 2017; published: Jun. 14th, 2017

ABSTRACT

The distribution of system damp could be described by the internal friction and structure damped coefficient. It was important for design of reducing vibration of the damping structure. The damping coefficient of cantilever thin plate was identified by the frequency response function matrix method in this paper. The principle and test process were introduced. The test system was built to identify the damping coefficient. The thin plate was analyzed by the system. The data of the plate root were all bigger than that of freedom end no matter the damping matrix was inherent friction or the structural damping coefficient. The inner friction coefficient of low frequency band was bigger, while the structural damping coefficient of high frequency band was bigger.

Keywords:Frequency Response Function, Matrix Method, Thin Plate, Damping Coefficient

基于频响函数矩阵法的薄板结构阻尼系数识别

朱全军1，樊习英2，曹枚根3，韩清鹏4，任建兴4，李天成4

1全球能源互联网研究院，北京

2国网山西省电力公司经济技术研究院，山西 太原

3中国电力科学研究院，北京

4上海电力学院能源与机械工程学院，上海

收稿日期：2017年5月25日；录用日期：2017年6月7日；发布日期：2017年6月14日

摘 要

机械系统的粘性或结构阻尼系数可以从空间上描述系统的阻尼分布，这对于阻尼结构减振设计具有重要的意义。本文研究基于频响函数矩阵法来辨识悬臂薄板结构系统阻尼系数。详细叙述了频响函数矩阵法的原理和测试流程。在此基础上组建了辨识结构系统阻尼系数的测试系统，对薄板结构进行了测试分析。从识别的阻尼矩阵可以看出，无论是粘性阻尼还是结构阻尼，薄板根部的数值均大于自由端的数值。比较不同频带的阻尼系数，可以看出在低频段粘性阻尼系数较大，而在高频段结构阻尼系数较大。

关键词 :频响函数，矩阵法，薄板结构，阻尼系数

Copyright © 2017 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

机械系统的阻尼减振降噪技术离不开对结构的阻尼测试。阻尼测试是验证阻尼模型正确性、检验阻尼减振效果以及实施阻尼结构优化设计的重要技术基础。识别阻尼的方法包括频域法 [1] 、时域法 [2] 、能量法 [3] 等，其中半功率带宽法和自由振动衰减法是识别结构系统阻尼特性的经典方法。

传统上，通常用阻尼比、模态损耗因子、品质因子等来描述系统的阻尼特性，这些参数一般对应着某阶模态，用半功率带宽法可以求出具体的阻尼参数。但是，对于阻尼减振设计，单用阻尼比还不能满足研究需要。主要因为阻尼比不能从空间上描述系统的阻尼分布，也不能明确反映作用在系统上的阻尼机理。

要从空间上描述系统的阻尼分布，可以考虑用阻尼系数来表征。本文研究基于频响函数矩阵法来辨识悬臂薄板结构系统阻尼系数的方法，详细叙述了频响函数矩阵法的原理和测试流程，并用数值模型进行了验证。在此基础上组建了阻尼系数辨识测试系统，对实际结构进行测试，并对测试结果进行了分析，最后，对该识别算法的有效性进行了评价。

2. 频响函数矩阵法识别阻尼系数的原理

所谓频响函数矩阵法是通过测量获得结构系统的频响函数，再对频响函数应用相应的辨识算法来识别出系统的阻尼矩阵。阻尼矩阵可以描述系统的阻尼类型、阻尼大小、阻尼分布等特征，因而用阻尼矩阵来表征系统的阻尼特性，可以用于指导阻尼减振设计。另外，测试的阻尼矩阵还可以用于阻尼结构系统的动力学建模与分析。相对于质量及刚度，很难用一个合适的阻尼模型来预估出系统的阻尼特性，因而将测试获得的阻尼矩阵引入到动力学有限元分析中，可以提高结构系统动力学分析的精度。频响函数矩阵法又可分为基于动柔度矩阵 [4] 和基于动刚度度矩阵 [5] 的识别。本文使用动刚度度矩阵的识别方法来完成阻尼系数的识别。

2.1. 基于动刚度矩阵的识别原理

该识别算法是针对既具有粘性阻尼又具有结构阻尼的动力学系统进行阻尼系数辨识，其动力学方程可描述为

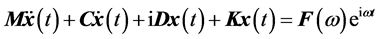(1)

这里是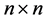矩阵，描述的分别是系统的质量、粘性阻尼、结构阻尼和刚度矩阵。

假设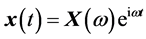，代入到方程(1)，可以得到

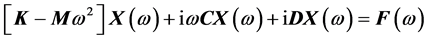(2)

动刚度矩阵定义为

(3)

这里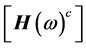是频响函数矩阵(FRM)，定义为

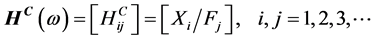(4)

实际应用中，总是先测试出频响函数，进一步通过求逆获得动刚度。

方程(3)的动刚度又可以分为实部及虚部

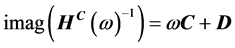(5)

(6)

方程(5)和(6)又可以进一步写成

(7)

(8)

2.2. 基于动刚度矩阵的识别流程

标记测量点，n个测量点，则需要个频响函数；测量频响函数，获得频响函数矩阵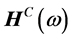，分解为实部及虚部。由方程(7)可获得阻尼矩阵的求解式

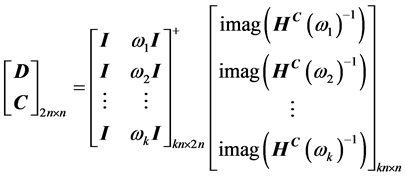(9)

假如有必要，刚度和质量矩阵也可以被求出

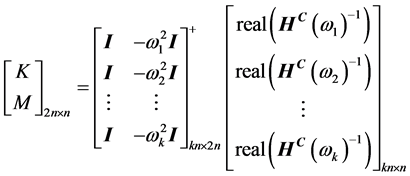(10)

假如仅用粘性阻尼来表示系统的阻尼特性，一个等价粘性阻尼矩阵Ceq求解式为

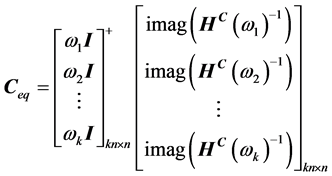(11)

假如仅用结构阻尼来表示系统的阻尼特性，一个等价粘性阻尼矩阵求解式为

(12)

3. 识别算法的模型校验理论

(1) 理论模型

图1为一个三自由度集中质量系统，相应的参数见表1。通过计算得出系统的频响函数，进一步利用频响函数反推出系统中的阻尼矩阵，从而检验算法的有效性。

(2) 识别算法校验

利用基于动刚度矩阵的识别算法进行校验。识别出的阻尼矩阵如表2所示。可见用频响函数识别出的阻尼矩阵与预设的相同，证明识别算法是有效的。

4. 钛基薄板悬臂结构阻尼系数识别

将TC4钛基薄板作为金属基层，其几何参数为长100 mm，宽80 mm，厚1.5 mm。材料参数为杨氏模量、泊松比、密度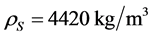。涂敷ZrTiN涂层，涂层厚度20μm。ZrTiN材料的密度为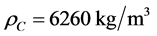。通过振动梁法可计算ZrTiN涂层材料的弹性模量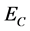和损耗因子。

4.1. 钛基薄板悬臂梁阻尼系数识别

搭建实验系统对涂层前后钛基悬臂薄板模态参数进行测试。分别对涂层前后钛基薄板梁进行测试，移动力锤敲击钛合金薄板，敲击顺序与电涡流传感器布置顺序一致，最后获得4 × 4的频响函数矩阵。针对测量点和敲击点进行测试，每点测试3次，取平均值作为测试结果，完成测试，如图2所示。

由于能量的衰减，力锤激励对于所研究的实验结构仅能达到3000 Hz，且仅在大约1000 Hz内能实现较高信噪比的测试。图1为试验敲击获得的频响，从中可以看出，大约1000 Hz以内存在三阶固有频率。

4.2. 实验结果

选择0~1000 Hz为测试范围，根据频响函数测试结果可知，该频段范围共包括了3阶固有频率。根据每阶固有频率的位置，将0~1000 Hz分成0~200 Hz、201~600 Hz、601~1000 Hz三个部分。受试验条件和试验设备的制约，试验测试所得钛合金薄板的频响函数是非对称矩阵，而理想状态下，在对应的激励点和响应点处获得的频响函数是相同的。例如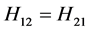：。于是将试验测得的频响函数进行对称化，令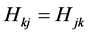取(,)，为测试点个数。利用动刚度矩阵法计算涂层前后钛基薄板在每个

Figure 1. Concentrate mass system with three degrees of freedom

图1. 三自由度集中质量系统

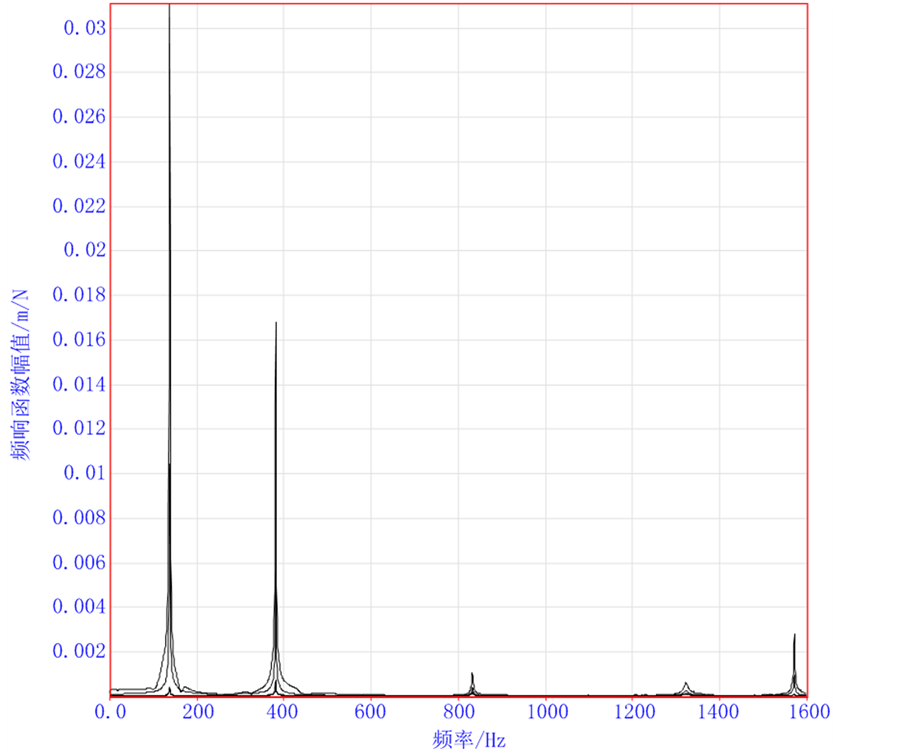
Figure 2. Frequency response of thin plate with titanium coating

图2. 钛基薄板频响函数图

Table 1. Parameters of concentrate mass system with three degrees of freedom

表1. 三自由度系统参数表

频段下的阻尼系数，结果见表3、表4。

从识别结果可以看出：以悬臂薄板结构系统中，阻尼主要来自于结构阻尼，结构阻尼系数大约比粘性阻尼系数大两个数量级。结构阻尼的产生主要源于薄板装卡产生的结合部界面摩擦阻尼和材料内耗。而从实验中可以看出材料内耗阻尼份额较小，因而无法用上述识别方法比较涂层前后阻尼系数的大小。

Table 2. Two different methods to solve the damping matrix of three degrees of freedom

表2. 两种算法求解三自由度系统的阻尼矩阵

Table 3. Recognization of damping coherence of thin plate without titanium coating by the symmetrical dynamic stiffness matrix method

表3. 利用对称动刚度矩阵识别未涂层钛基薄板的阻尼系数

Table 4. Recognization of damping coherence of thin plate with titanium coating by the symmetrical dynamic stiffness matrix method

表4. 利用对称动刚度矩阵识别涂层后钛合金薄板的阻尼系数

从识别的阻尼矩阵可以看出，无论是粘性阻尼还是结构阻尼，薄板根部的数值均大于自由端的数值。比较不同频带的阻尼系数，可以看出在低频段粘性阻尼系数较大，而在高频段结构阻尼系数较大。

5. 结论

机械系统的粘性或结构阻尼系数可以从空间上描述系统的阻尼分布，这对于阻尼结构减振设计具有重要的意义。本文研究基于频响函数矩阵法来辨识悬臂薄板结构系统阻尼系数。

详细叙述了频响函数矩阵法的原理和测试流程。用一个三自由度的集中质量模型，做了原理性验证。结果表明：用频响函数识别出的阻尼矩阵与预设的相同，证明识别算法是有效的。对涂层前后钛基悬臂薄板模态参数进行测试。力锤激励对于所研究的实验结构仅能达到3000 Hz，且仅在大约1000 Hz内能实现较高信噪比的测试。通过对称动刚度矩阵可以识别涂层后钛合金薄板的阻尼系数。

基金项目

由国家电网科技项目(SGRI-WD-71-15-010)支持。

文章引用

朱全军,樊习英,曹枚根,韩清鹏,任建兴,李天成. 基于频响函数矩阵法的薄板结构阻尼系数识别
Recognition of Structural Damping Coefficient of Thin Plate Based on the Frequency Response Matrix Method[J]. 机械工程与技术, 2017, 06(02): 133-139. http://dx.doi.org/10.12677/MET.2017.62019

参考文献 (References)

  1. 1. 李敏花, 柏猛, 吕英俊. LM算法在二阶过阻尼系统参数估计中的应用[J]. 自动化仪表, 2016, 36(7): 90-93.

  2. 2. 胡钢墩, 李发泽. 惯性系统的时域在线辨识[J]. 控制与决策, 2010, 25(1): 133-136.

  3. 3. 陈俊杰, 高康华, 孙敖. 爆炸条件下结构超压-冲量曲线简化计算研究[J]. 振动与冲击, 2016, 35(13): 224-232.

  4. 4. Lee, J.-H. and Kim, J. (2001) Identification of Damping Matrices from Measured Frequency Response Functions. Journal of Sound and Vibration, 240, 545-556.

  5. 5. Lee, J.-H. and Kim, J. (2001) Development and Validation of a New Experimental Method to Identify Damping Matrices of a Dynamic System. Journal of Sound and Vibration, 246, 505-524.

期刊菜单