Mechanical Engineering and Technology
Vol.
08
No.
02
(
2019
), Article ID:
29903
,
7
pages
10.12677/MET.2019.82015
The Rolling Bearing Fault Feature Extraction Method Based on Wavelet Packet Noise Reduction and VMD
Yanhong Yuan, Jingguo Bai, Yongshuai Wang
Beijing Building Materials Testing Academy Co., Ltd., Beijing
Received: Apr. 3rd, 2019; accepted: Apr. 18th, 2019; published: Apr. 25th, 2019

ABSTRACT
Aiming at the problem that a large amount of random noise mixed in the rolling bearing vibration signals and its nonlinear non-stationary, and that the fault features of vibration signal are difficult to extract, the noise reduction based on wavelet packet and VMD rolling bearing fault feature extraction method was proposed. Firstly, this method uses the wavelet packet de-noising to process the signal to filter out the noise in the signal component; then, the VMD method is used to decompose the signal after noise reduction; finally, the obtained with the original signal have the largest correlation components for the Hilbert demodulation, so as to extract the fault feature. Finally, the IMF that has the largest correlation with original signal was analyzed by Hilbert envelope, so as to extract the fault feature. Experimental results show that the rolling bearing fault feature extraction method based on Wavelet Packet noise reduction and VMD can effectively extract the fault feature and realize the fault diagnosis of rolling bearing.
Keywords:Wavelet Packet, VMD, Rolling Bearing, Fault Diagnosis
基于小波包降噪与VMD的滚动轴承故障特征提取方法
袁燕红,白静国,王永帅
北京建筑材料检验研究院有限公司,北京
收稿日期:2019年4月3日;录用日期:2019年4月18日;发布日期:2019年4月25日

摘 要
针对滚动轴承振动信号掺杂有大量随机噪声且自身的非线性非平稳性,致使振动信号中故障特征难以提取的问题,提出基于小波包降噪与VMD的滚动轴承故障特征提取方法。该方法首先将采集到的滚动轴承故障振动信号经过小波包降噪处理,滤除信号中的噪声成分;后利用VMD方法对降噪后信号进行分解,将信号中的故障成分与原有信号成分剥离;最后对分解后所得与原信号有最大相关性的分量进行Hilbert解调,从而提取出故障特征。实验结果表明,基于小波包降噪与VMD的滚动轴承故障特征提取方法能够有效提取出故障的特征成分,实现滚动轴承的故障诊断。
关键词 :小波包,VMD,滚动轴承,故障诊断

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
滚动轴承在机械设备中为旋转体提供可靠支撑并保证设备有序运行,且其作为重要零部件在各行各业中有着广泛的应用范围。然而,由于运行环境的恶劣与运转中应力集中等因素作用,滚动轴承也成为了一个易损零部件。若其发生故障,易造成设备运行不良,且故障的扩展甚至会导致整台设备及整条生产线的停产,从而造成重大经济损失。因此,对滚动轴承进行故障诊断,对保证设备正常运行有着重要的作用。
近年来,越来越多专家及学者致力于基于滚动轴承振动信号的故障诊断。文献 [1] 将列车滚动轴承振动信号进行EMD分解后,利用相关系数法估计安全域边界并进行故障诊断。研究结果表明该方法能较好判断轴承的运行状况;文献 [2] 将齿轮故障振动信号经过EMD分解后,提取分解后所得IMF的时域与能量特征输入支持向量机实现齿轮不同状态的识别,实现齿轮箱的故障诊断;文献 [3] 使用VMD方法将滚动轴承振动信号分解后,对敏感分量进行包络谱分析,从而判断轴承的故障类型与严重程度;文献 [4] 应用变分模态分解(variational mode decomposition, VMD)算法对微弱故障信号进行分解,然后选取峭度值最大的IMF分量进行变尺度多稳随机共振,实现滚动轴承的故障特征提取。
然而,由于EMD方法的模态混叠效应等缺陷,以及在VMD分解之前信号中夹杂有大量随机噪声等原因,必然会导致分解后所得IMF分量信号的混乱,进而影响故障信号特征的提取。因此,本文提出基于小波包降噪与VMD的滚动轴承故障特征提取方法。该方法首先利用小波包对滚动轴承的振动信号进行降噪处理,滤除信号中的随机噪声等的一些干扰成分,得到包含有故障特征的较为精纯的信号;然后,利用VMD方法对降噪后信号进行分解,得到一系列包含有信号故障特征等成分的本征模式分量;最后,利用相关系数法对各IMF进行评估,选取与降噪后信号相关程度最大的IMF进行Hilbert包络解调分析,提取出滚动轴承故障特征。实验结果表明,该方法能够准确提取信号故障特征,实现滚动轴承的故障诊断。
2. 小波包降噪
小波包 [5] [6] 这一函数簇构造出了平方可积实数空间的规范正交基库。其中,小波包分解结构如图1所示,其中AAA3、ADA3、AAD3和ADD3为第三层节点的低频系数,而DAA3、DDA3、DAD3和DDD3为第三层的高频系数。
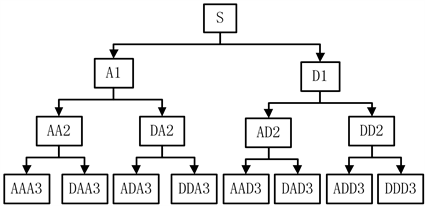
Figure 1. Decomposition of wavelet packets
图1. 小波包分解
小波包降噪的具体步骤为:
1) 选择一个小波基并确定分解层次N,然后对信号进行N层小波包分解;
2) 计算最佳树(即确定最佳小波包基),对一个给定的熵标准,计算最佳小波包分解树;
3) 对各个分解尺度下的高频系数选择一个适当的阈值进行阈值量化处理。为得到最优结果以满足特定的分析和信息评价标准,阈值通过反复实验不断调整来确定;
4) 根据第N层的小波包分解低频系数和量化处理系数进行小波重构。
3. 变分模式分解(VMD)
VMD是一种通过搜寻约束变分模型最优解来分解信号并得到本征模态分量(IMF)的自适应分解方法。其实质是变分问题的构造和求解 [7] [8] 。
3.1. 构造变分问题
假设一个信号被VMD算法分解,得到K个窄带IMF,则变分问题构造过程为:
1) 用希尔伯特方法对各个IMF进行处理得到解析信号;
(1)
2) 混合一个预估的中心频率 并移频。
(2)
3) 计算梯度的平方范数即对解调信号做高斯平滑处理,则约束变分问题可表示为:
(3)
式中, 为第K个模态; 为第K个模态中心频率。
3.2. 求解变分问题
为了求解变分问题,首先转化为无约束优化问题,并引入二次惩罚因子α和拉格朗日乘法算子 ,其增广拉格朗日表达式为:
(4)
VMD运用了乘法算子交替方向法,通过轮替更新 , 和 求得拉格朗日表达式的“鞍点”。变分问题的解 在频率内表示如下:
(5)
其中 分别代表 的傅里叶变换,在公式(3)中包含维纳滤波器结构。各模态时域信号可以通过对滤波后的信号做傅里叶逆变换取实部求得。
更新后的各模态中心频率可以通过式(6)求得:
(6)
4. 实验分析
本文采用美国凯斯西储大学电气工程与计算机科学系的滚动轴承实验台(如图2)所测实验数据进行分析,以验证基于小波包降噪与VMD的滚动轴承故障诊断方法的有效性,测试轴承为驱动端6205-2RS深沟球轴承,且故障出现在轴承外圈,经故障频率核算公式计算得到故障频率为105.56 Hz。轴承节径为39.04 mm,滚动体直径为7.94 mm,滚动体接触角为0˚,滚动体个数为9,轴承转速为1750 r/min,采样频率为12 kHz,且选用驱动端轴承处采集到的滚动轴承振动加速度信号的4096个采样点作分析,其时域波形如图3所示。

Figure 2. Test bench of Fault simulation for rolling bearing
图2. 滚动轴承故障模拟实验台
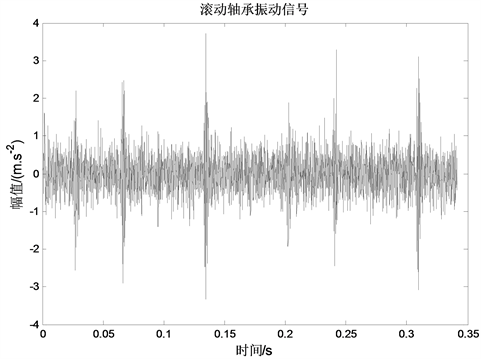
Figure 3. Original vibration signal of outer ring fault for rolling bearing
图3. 滚动轴承外圈故障原始振动信号
1) 首先,使用小波包方法对信号进行降噪处理,本文选用小波包基函数为db7,分解层数为3层,对分解后所得的8个小波包节点采用默认阈值降噪,后将处理后各个节点进行重构后形成降噪后信号。图4为滚动轴承降噪后信号。从图易见,图4中信号谱线比图3中谱线更为清晰,且通过计算得到降噪后信号信噪比达到4.5124,说明小波包方法有效滤除了滚动轴承振动信号中的噪声成分,凸显出了信号的有用成分。
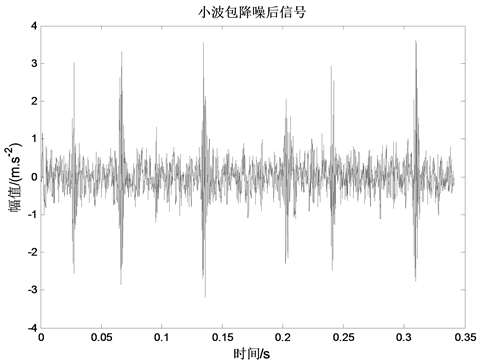
Figure 4. Signal after of outer ring noise reduction for rolling bearing
图4. 滚动轴承外圈降噪后信号
2) 为将降噪后信号中各组成成分进行划分,对降噪后信号做VMD分解,其中VMD方法中根据中心频率相近原则设定模态数K = 5,惩罚因子 ,拉格朗日乘子 ,图5为VMD分解后所得部分IMF分量。从图可以看出,信号的各成分被清晰的分解到了各个不同的频带上,有效的将故障成分与设备固有振动等成分进行了区分。
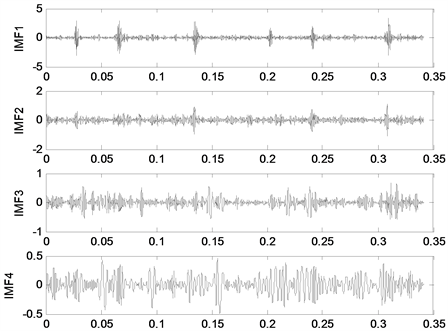
Figure 5. Part of IMF weight after VMD decomposition
图5. VMD分解后部分IMF分量
3) 将分解后所得各IMF分量与降噪后信号做互相关分析,选取相关系数最大即包含有信号最多有用信息(即最多故障冲击成分)的IMF2分量进行Hilbert包络解调变换,得到图6所示结果。从图中可以看出,谱线中105.5 Hz处出现明显的波峰值,与滚动轴承外圈故障特征频率基本吻合。且在故障频率的2倍频210.9 Hz及3倍频316.4 Hz处也出现了较为清晰的波峰,Hilbert包络解调方法成功提取出了故障特征频率。
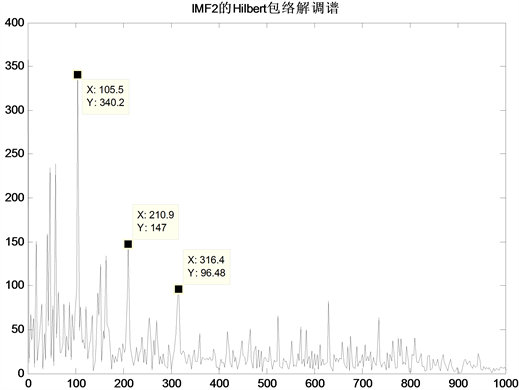
Figure 6. Hilbert envelope demodulated spectrum of IMF2
图6. IMF2经Hilbert包络解调后谱图
5. 结论
本文利用小波包方法对滚动轴承振动信号进行降噪处理,并对降噪后信号做VMD分解,最后利用Hilbert包络解调方法对VMD分解后与原信号相关度最大的本征模式分量进行分析。实验结果表明,基于小波包降噪与VMD的滚动轴承故障诊断方法能够准确提取故障特征,实现滚动轴承的故障诊断。
文章引用
袁燕红,白静国,王永帅. 基于小波包降噪与VMD的滚动轴承故障特征提取方法
The Rolling Bearing Fault Feature Extraction Method Based on Wavelet Packet Noise Reduction and VMD[J]. 机械工程与技术, 2019, 08(02): 118-124. https://doi.org/10.12677/MET.2019.82015
参考文献
- 1. 杨琦, 陈智才. 基于EMD和相关系数法的列车滚动轴承故障诊断方法研究[J]. 电力机车与城轨车辆, 2018, 41(3): 15-23.
- 2. 王建国, 刘永亮, 等. 基于EMD与多特征的支持向量机故障诊断[J]. 机械设计与制造, 2015, 10(10): 65-67.
- 3. 昝涛, 庞兆亮, 等. 基于VMD的滚动轴承早期故障诊断方法[J]. 北京工业大学学报, 2019, 45(2): 103-110.
- 4. 时培明, 苏晓, 等. 基于VMD和变尺度多稳随机共振的微弱故障信号特征提取方法[J]. 计量学报, 2018, 39(4): 515-520.
- 5. 孙伟, 熊邦书, 等. 小波包降噪与LMD相结合的滚动轴承故障诊断方法[J]. 振动与冲击, 2012, 31(18): 153-156.
- 6. 熊星. 基于小波包分解和希尔伯特黄变换的滚动轴承故障诊断[D]: [硕士学位论文]. 合肥: 中国科学技术大学, 2014.
- 7. 刘长良, 武英杰, 甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报, 2015, 35(13): 1-8.
- 8. 安邦, 潘宏侠, 等. 应用VMD和多参数融合的齿轮箱故障诊断[J]. 组合机床与自动化加工技术, 2017, 4(4): 92-95.