Statistics and Application
Vol.06 No.05(2017), Article ID:23239,6
pages
10.12677/SA.2017.65062
Analysis of Measles Incidence Based on Time Series
Dan Zhou
School of Mathematics & Physics Science and Engineering, Anhui University of Technology, Maanshan Anhui

Received: Dec. 6th, 2017; accepted: Dec. 22nd, 2017; published: Dec. 29th, 2017

ABSTRACT
Based on the national measles morbidity data from 1950 to 2014, we establish a model to effectively predict the incidence of measles in the short term through the time series analysis method, so as to issue warnings on the epidemic situation of measles and prepare the preventive work in advance.
Keywords:Time Series, Measles, Exponential Smoothing
基于时间序列的麻疹发病率分析
周丹
安徽工业大学数理科学与工程学院,安徽 马鞍山
收稿日期:2017年12月6日;录用日期:2017年12月22日;发布日期:2017年12月29日

摘 要
基于1950年~2014年的全国麻疹发病率数据,利用时间序列建立模型,有效预测短期内麻疹的发病率,为麻疹的流行情况进行预警,提前做好预防工作。
关键词 :时间序列,麻疹,指数平滑法

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
时间序列 [1] 是按时间顺序排列的,随时间变化且相互关联的数据序列。从统计意义上看,时间序列就是将某一个指标在不同时间上的不同数值,按时间顺序排列的数列。时间序列有以下特点:第一,时间序列中的数值或数据点的位置与时间有关,即数据的取值依赖于时间的变化,但不一定是时间t的严格函数;第二,每一时刻的取值或数据点的位置具有随机性,不能完全用历史值预测;第三,前后时刻(不一定是相邻时刻)的数值或数据点的位置有一定的相关性(系统的动态规律性);第四,从整体上看,时间序列往往具有某种趋势性或周期性变化。
时间序列分析方法分为描述性时间序列分析和统计性时间序列分析,描述性时间序列分析是指通过直观的数据比较,寻找时间序列的内在规律;统计性时间序列分析又可以分为频域分析法和时域分析法,频域分析法是把时间序列看作互不相关的周期(频率)分量的叠加,通过研究各分量的周期变化,以充分揭示时间序列的规律;时域分析法的基本思想是:序列值之间存在着一定的相关关系,这种相关关系具有一定的统计规律,我们的目的就是寻找这种规律,并构建数学模型来描述这种规律,进一步利用这个模型来预测序列未来的走势。
时域分析法最早产生于1927年,由英国统计学家尤尔提出了自回归模型,1931年,英国数学家、天文学家沃克提出了移动平均模型和自回归移动平均模型。1970年,美国统计学家博克斯与英国统计学家詹金斯合著了《时间序列分析、预测与控制》。1982年,美国统计学家、计量经济学家恩格尔提出了自回归条件异方差模型。1985年博勒斯洛夫提出了广义自回归条件异方差模型。1987年,英国统计学家、计量经济学家格兰杰提出了协整理论,为多变量时间序列建模拓宽了条件,使得“变量是平稳的”不再是必需条件。
2. 主要内容
2.1. 背景
麻疹 [2] 是现今儿童非常常见的急性呼吸道传染病之一,它的传染性很强,特别是在人口密集但没有普种疫苗的地区易发生流行。麻疹病毒属于副黏液病毒,通过呼吸道分泌物飞沫传播。其发病特征是:发热、上呼吸道炎症、眼结膜炎及皮肤出现红色斑丘疹和颊黏膜上有麻疹黏膜斑,疹退后遗留色素沉着伴糠麸样脱屑。常并发呼吸道疾病如中耳炎、喉–气管炎、肺炎等,麻疹脑炎、亚急性硬化性全脑炎等严重并发症。目前尚无特效药物进行治疗。
本文研究旨在利用历年的麻疹监测数据,通过曲线拟合和参数估计建立数学模型,对麻诊发病进行预测和预警,为麻疹的预防控制提供理论依据 [3] 。
2.2. 数据来源
本文的数据资料来自公共卫生科学数据中心,其采集了从1950年到2014年期间,北京市,安徽省,河北省等三十多个省市地区的发病人数,死亡人数,发病率以及死亡率。
首先,我们来看一下从1950年到2014年期间,全国的麻疹 [4] 发病率和死亡率如图1,图2所示,我们可以看出在1956年之前,麻疹的发病率呈直线上升趋势,但死亡率呈周期性变化,在1956年到1974
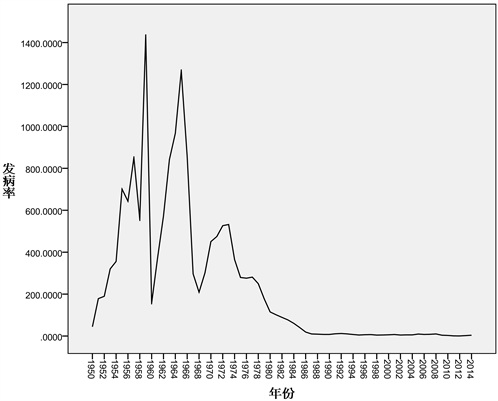
Figure 1. Morbidity time series chart
图1. 发病率时间序列图
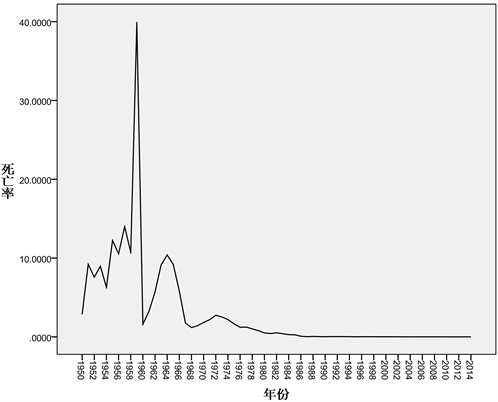
Figure 2. Mortality time series chart
图2. 死亡率时间序列图
年之间,麻疹发病率和死亡率呈周期性波动,从1974年到2014年,麻疹的发病率以及死亡率逐渐减小,趋于一个定值。下面我们就全国麻疹发病率数据进行研究。
2.3. 模型
20世纪60年代,George Box与Gwilym Jenkins提出了一种关于时间序列分析、预测的方法,称之为B-J模型,也叫做ARMA (Auto Regression Moving Average)模型。ARMA模型 [5] 的基本模型有三种情况:自回归模型(AR模型);滑动平均模型(MA模型);自回归滑动平均模型(ARMA模型) [6] 。
下面介绍一下指数平滑法 [7] ,这是一种加权移动平均,即可以用来描述时间序列的变化趋势,也可以实现时间序列的预测。它实现预测的基本原理是:用时间序列过去取值的加权平均来作为未来的预测值,离当前时间越近,它的权重就越大。
其模型的数学表达式为:对于一个时间序列 ,满足:
其中, 表示时间序列第 时刻的预测值, 表示时间序列在第 时刻的实际观测值, 表示时间序列在第 时刻的预测值, 表示平滑系数,其中 。
下面我们对每年全国麻疹发病率进行拟合,则模型统计指标如表1,表2所示。
我们可以看一下2010年到2014年的真实值与预测值(置信区间为95%)如表3所示。
如图3所示,我们可以看出,拟合效果较好。且模型参数 的估计值为0.491。
2.4. 结论
由上述的模型,我们可以很好的预测短期麻疹发病率,并基于所得到的预测值进行麻疹预防工作 [8] ,有效防止麻疹的传染,并对麻疹病人进行有效治疗与控制,不过我们的模型还可以进一步的改进,使预测值更加准确。我们可以观察一下我国各个省份的麻疹发病率如图4所示。
从图4可以看出,不同的地域,麻疹的发病率并不相同,前期,上海,北京的麻疹发病率明显高于其他地区,但后期的麻疹发病率低于其他地区,其原因可能与人口密集度有关,由于北京和上海的人口密度明显大于其他地区,人口流动性也最快,后期由于其医疗水平提升的最快,所以麻疹的发病率低于其他地区,当然麻疹的发病率也有其他原因,还需要我们进一步研究。
Table 1. Model statistics
表1. 模型统计量
Table 2. Exponential smoothing model parameters
表2. 指数平滑法模型参数
Table 3. Predictors and actuals
表3. 预测值与实际值
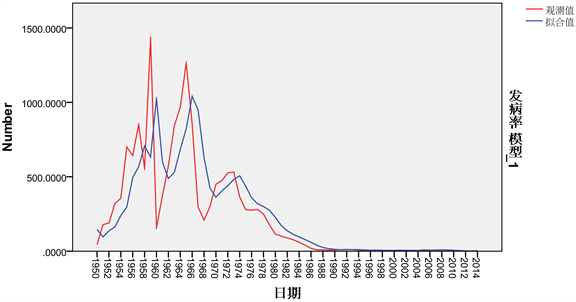
Figure 3. Observation charts
图3. 观测统计图
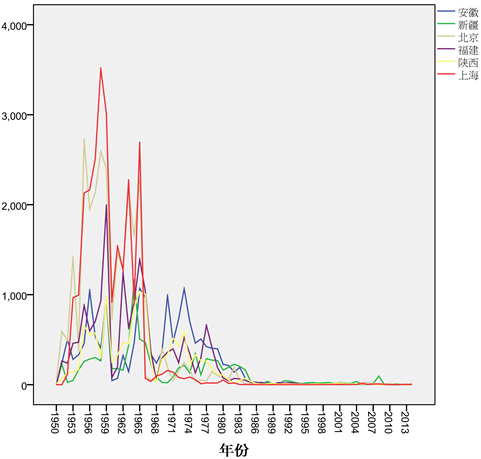
Figure 4. Measles incidence map around
图4. 各地麻疹发病率统计图
致谢
感谢我的导师对我的悉心教导,感谢我的同学和朋友在学习、生活上的关心和帮助,最后,感谢我的家人,一直以来,无论是学习和生活,都离不开他们的支持、照顾和理解。
基金项目
安徽工业大学研究生创新基金资助(2016137)。
文章引用
周 丹. 基于时间序列的麻疹发病率分析
Analysis of Measles Incidence Based on Time Series[J]. 统计学与应用, 2017, 06(05): 550-555. http://dx.doi.org/10.12677/SA.2017.65062
参考文献 (References)
- 1. Glass, K., Xia, Y. and Grenfell, B.T. (2003) Interpreting Time-Series Analyses for Continuous-Time Biological Models—Measles as a Case Study. Journal of Theoretical Biology, 223, 19-25. https://doi.org/10.1016/S0022-5193(03)00031-6
- 2. 田鑫, 陈超, 等. 应用时间序列模型预测麻疹疫情[J]. 中国疫苗和免疫, 2008, 14(3): 229-233.
- 3. 刘曙光, 王立芹, 等. 河北省麻疹疫情时间序列的预测和预警分析[J]. 中国卫生检验杂志, 2015, 25(17): 2954-2956.
- 4. 丁晓艳, 彭志行, 等. 运用时间序列模型对麻疹流行趋势的预测与分析[J]. 南京医科大学学报, 2011, 31(8): 1200-1203.
- 5. 姜乐. 基于时间序列的股票价格分析研究与应用[D]: [硕士学位论文]. 大连: 大连理工大学, 2015.
- 6. 郑彦玲, 秦伶俐, 张利萍. 基于随机时间序列法的新疆麻疹发病率预测[J]. 数学的实践与认识, 2012, 16(42): 178-184.
- 7. 骆方, 刘红云. SPSS数据统计与分析[M]. 北京: 清华大学出版社, 2011.
- 8. 刘曙光, 王立芹, 等. 河北省流行性腮腺炎SARIMA模型预测分析[J]. 医学动物防制, 2015, 31(9): 968-970.
