Statistics and Application
Vol.07 No.03(2018), Article ID:25597,10
pages
10.12677/SA.2018.73039
Forecast of Income Gap between Urban and Rural Residents in Hunan Province
—A Study Based on ARIMA-GM Combination Model
Wenxin Qu, Xiangdong Liu
Jinan University, Guangzhou Guangdong
Received: Jun. 3rd, 2018; accepted: Jun. 20th, 2018; published: Jun. 27th, 2018

ABSTRACT
The income gap between urban and rural areas has always been a key issue in the five-year plan. In this article, by collecting the quarterly data of urban and rural residents’ income in Hunan Province from 2004 to 2017, we establish and compare the seasonal multiplicative ARIMA model, GM(1,1) model, and ARIMA-GM combined model, finally the ARIMA-GM combination model is applied to analysis and forecast the urban-rural income gap in Hunan from 2018 to 2019. The result shows that the ARIMA-GM combination model can solve the problem of estimating and predicting the income gap in Hunan province, and the prediction accuracy is high, so as to provide an important basis for the government to formulate relevant policies.
Keywords:Urban-Rural Income Gap, Multiplicative Seasonal ARIMA Model, GM(1,1) Model, ARIMA-GM(1,1) Combination Model, Forecast
湖南省城乡居民收入差距预测
—基于ARIMA-MA模型
屈文鑫,柳向东
暨南大学,广东 广州
收稿日期:2018年6月3日;录用日期:2018年6月20日;发布日期:2018年6月27日

摘 要
城乡收入差距问题一直是五年规划中重点问题。文章采用湖南省2004年至2017年城乡居民收入的季度数据,分别利用季节乘法ARIMA模型、GM(1,1)模型和ARIMA-GM组合模型建模并检验和比较,最后将模型应用于湖南省2018年至2019年城乡收入差距预测与分析。结果表明,ARIMA-GM组合模型能够较好的解决收入差距的估计和预测问题,预测精度较高,从而为政府制定相关政策提提供重要依据。
关键词 :城乡居民收入差距,乘法季节ARIMA模型,GM(1,1)模型,ARIMA-GM组合模型,预测

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
“十三五规划”中,三农问题、收入分配仍然是亟待解决的热点问题。农民问题一直是制约生产力发展的一个重要因素,城乡居民收入差距是衡量我们经济社会发展的重要指标。分析和预测城乡居民收入差距的动态变化过程,一方面可以了解一个地区经济社会的发展平衡性,另一方面可以为国家科学制定发展农村经济的政策,缩小城乡差距,促进经济增长提供参考意见,有利于实现城镇化以及全面小康社会这一目标。
目前,针对城乡居民收入差距问题的研究,大多数学者利用的建模与预测分析方法主要是ARMA模型和GARCH模型。傅德红 [1] 主要以我国1978年至2007年城市人均可支配收入和农村人均纯收入时间序列数据为依据,分析了城乡收入差距的内在规律性,对其发展趋势进行了预测,并提出了合理的政策建议。涂雄苓 [2] 选取全国1978年至2010年的统计数据,建立ARIMA模型、灰色模型、二次多项式三个模型进行比较分析,最终得出二次多项式预测模型拟合效果更好的结论,用该模型对全国未来三年城乡居民收入差值进行了预测,并给出相应建议。学者辜子寅 [3] 根据江苏省1981年至2010年城乡收入差距指标数据,构建了ARMA-GM线性组合模型,对未来5年江苏省城乡居民收入差距进行预测和分析,并得出收入差距会呈现逐渐扩大趋势。龚承刚 [4] 等人选取湖北省1981年至2012年的城乡居民收入数据,建立城乡居民收入比的ARIMA模型,并对模型进行检验得出其模型预测效果较优的结论。最后利用该模型对2013年至2015年湖北省城乡居民收入比数据进行了短期外推预测。本文根据2004年至2017年湖南省城乡收入季度数据,从收入差距绝对值和收入差比两个方面入手,对湖南省城乡居民收入差距变动趋势建立ARIMA-GM组合模型,并对未来两年湖南省城乡居民收入差距进行短期预测。
2. 理论与方法
2.1. 季节乘法ARIMA模型
ARIMA模型,即求和–自回归–移动平均模型,简称B-J模型。在ARIMA模型中,变量的未来取值可以表达为过去若干取值和随机误差的线性函数,该模型自产生以来,已广泛应用于各领域。如时间序列在进行D阶季节差分前进行了d阶逐期差分后达到平稳,则可以建立随机季节模型与ARIMA模型的结合-ARIMA乘法季节模型。
与一般的季节模型相比,乘法季节ARIMA模型考虑到了ARIMA和季节影响的交互影响,可以用少量系数表示出交互作用产生影响的大量信息。一般将随机过程 定义为季节周期为s的乘法季节 ,则AR的特征多项式可表示为 ,MA的特征多项式表示为 ,其中B表示延迟算子,则
若时间序列 为非平稳时间序列,首先对此序列进行差分平稳化,对 做周期为s的季节差分,用 表示,定义:
(1)
随机过程 为季节周期s的乘法季节 ,则序列
(2)
满足季节周期s的乘法季节 。其中 表示 的k步差分; 表示 的d阶差分。
2.2. 分组GM(1,1)模型
灰色预测是灰色系统理论的一个重要内容,对解决灰色系统的趋势预测具有独到的优势,尤其是社会经济方面。大部分学者以往的做法即在模型中引入季节指数,用模型预测结果乘以相应季节指数作为最后的预测结果。但是这种方法往往对于一些季节波动较大的样本数据效果并不是很好,为了避免这一问题出现,汪潘义 [5] 等学者提出分组灰色预测法,对每组数据都建立相应的GM(1,1)模型来消除季节趋势这一影响因素。
第一步:将数据按季度分成四组新的时间序列 , 表示第i季度的原始数据系列。分别对各季度序列建立相应的GM(1,1)模型。
第二步:作1阶累加生成
第三步:确定数据矩阵 ,其中
,
第四步:求出参数列
第五步:得到时间响应系列 ,然后确定 的值 得还原数列:
(3)
第六步:进行后验差检验。设原始序列标准差为 ,残差序列标准差为 ,则均方差比值 ,对于指定的 ,当 时,该模型为均方差比合格。小误差概率 ,模型的精度由C和p共同刻画,精度等级如表1所示。
Table 1. Model accuracy
表1. 模型精度
2.3. ARIMA-GM组合模型
线性组合模型的基本形式可以写成:
(4)
其中 表示单独的某种方法的预测值, 表示第i种方法预测值的权重。组合预测模型中权重的获取一直都是重点和难点,合理有效的权重分配会大大地提高预测精度。从模型的拟合方面来说,可以从误差的角度来确立模型的权重,常用的误差统计量有相对误差、拟合误差、对数误差和绝对误差。一般的权重方法即以某一种误差作为评判标准,分别计算每一种模型的误差值,按照从小到大排序,误差大的赋予较小的权重,误差小的赋予较大的权重。李佩 [6] 研究表明组合权重的方法往往使得组合模型比单种误差权重,拥有更小的误差。本文参考该方法,探讨在平均绝对百分数误差和均方根误差的基础上的组合权重计算方法。
平均绝对百分数误差是一种相对误差,表示预测误差占实际值的比重,通常用来作为准确度的衡量标准,它的计算公式为 。均方根误差表示的是误差平方和的均值,通常体现了预测的精度,它的计算公式为 。其中 表示第t期的预测值, 表示第t期的真实值。若用 表示第i个模型的最终权重系数,则组合权重可表示为:
(5)
其中: 为第i个模型以MAPE为准则确立的权重系数; 为第个i模型由RMSE确定的权重系数。用此方法将MAPE权重系数和RMSE权重系数进行结合,对每一单个模型在组合模型的贡献程度给予两方面的制约。经过双重条件的筛选,使得MAPE与RMSE均较小的模型所占的优势更为明显,在组合模型中所占的权重较大,对组合模型的贡献程度也更高。最后拟合出来的组合模型表达式为:
(6)
3. 实证分析
3.1. 数据的来源与处理
为了能够真实的从多方面反映城乡居民收入差距实际水平,体现数据资料可比性、可操作性等原则,本文从绝对差和差比两个方面,选取我国湖南省2004年到2017年的城乡居民收入绝对差值(y1)和城乡居民收入差比(y2)两个指标的季度数据作为研究对象(表2)。其中2013年开始由于国家统计局不再使用农村居民人均现金收入这一指标,因此2012年之后的季度数据均使用农村居民人均可支配收入这一指标代替,数据来源中国宏观经济数据库。基于数据使用的不同目的,将所搜集到的数据分为两部分:一部分是湖南省2004年第一季度至2015年第四季度城乡居民收入差异数据(约85%的样本数据)作为训练集;另一部分是2016至2017年的数据(约15%的样本数据)作为测试集,最后选出误差最小的模型对未来一两年的收入差距进行短期预测。本文所有的结果均通过R 3.1.2计算得到。
由图1可知,从整体上看,2004~2017年湖南省城乡居民收入差距是呈不断扩大的趋势,第一季度
Table 2. Data of income gap between urban and rural areas in Hunan Province
表2. 湖南省城乡收入差距数据

Figure 1. Curve: income gap between urban and rural areas in Hunan Province
图1. 湖南省城乡收入差距折线图
差值最小,第四季度达到最大,呈现明显的季节趋势。城镇居民人均可支配收入从2004年第一季度的2583.8元增加到2017年第三季度的24,210.21元,增长了8.37倍,农村居民人均收入从2004年第一季度828.1元增长到2017年第三季度9071.46元,增长了9.95倍,均略低于全国平均城乡居民收入水平。而湖南省城乡居民收入差距比呈缓慢下降的趋势,2004~2009年城乡收入差距比徘徊在2.85左右,2010年湖南省开始实施中共中央一号文件“三农政策”,其中包括农业补贴等政策大大提高了农民的收入,因此城乡收入差比出现大幅度下降,降至2.45左右。2013年有所攀升,此后一直维持在2.65左右维持小幅度的缓慢下降趋势。可以看到,虽然湖南省城乡居民收入绝对差值不断扩大,但是城乡居民收入差比已经在不断的缩减,尤其是“十二五”规划期间,国家大力支持农村事业的发展,农民的生活水平得到不断的提高。湖南是个农业大省,农村人口占湖南省总人口的数的47.25%,低于全国平均水平,因此,提高农村居民收入,缩小城乡差距对于湖南省的发展有着至关重要的作用。
3.2. 乘法季节ARMIA模型的预测
3.2.1. 时间序列平稳化
通过图1可以知道,自2004年以来,湖南省城乡居民人均绝对差值呈现出不断提高的态势,且存在明显的周期现象,周期单位为4个单位。另外该省城乡居民人均差距比呈现缓慢下降的趋势,同样存在周期现象。可以知道,要保证序列的平稳性需要先对数据直接取差分或者对数之后取进行1阶差分,消除长期趋势,然后再进行4步差分消除季节效应。变化之后的序列基本平稳,周期性和增长趋势基本消除,做出新序列的自相关和偏自相关图(图2),对模型进行定阶和拟合。
3.2.2. 模型定阶和检验
观察图2自相关和偏自相关图,首先考虑1阶4步差分之后,显示4阶以内的样本自相关系数和偏自相关系数均不截尾。再考虑季节自相关特征,自相关系数的延迟4阶,延迟8阶,延迟12阶和延迟16阶均落在两倍标准差之外拖尾,显著不为0;偏自相关系数只有延迟4阶落在两倍标准差之外截尾,
显著不为0。综合以上差分信息,因此可考虑拟合 模型。为了保证模型选择的准确性,同时拟合了 , 和 三个模型,然后根据AIC、BIC准则选出最优的模型,最终确定 是最优的,各参数系数均通过检验,且AIC最小。因此,城乡收入差绝对数值的季节拟合模型表达式如下,其中B为延迟算子, 为残差:
(7)
对城乡收入绝对差值拟合的 进行Ljung-Box 检验,结果表明,在滞后阶数为
6,12的情况下,P值为0.8472和0.8286,均大于显著水平0.05,因此不能拒绝残差不存在自相关性的零假设。图3为拟合模型(1)残差的自相关系数和偏自相关系数图。图形显示,时间序列模型残差的
Ljung-Box统计量在滞后各期都没有显著的自相关,残差为白噪声过程。因此建立
模型来拟合2004年第一季度至2016年第四季度湖南省城乡居民收入绝对差值是充分的。
3.3. GM(1,1)模型的预测
对于表1中的数据,我们首先根据季度进行分组,按年度排成四个时间序列表。我们先计算第一季度的预测值。
设第一季度原始数列为 ,一次累加生成数据为 ,经计算, 时, ,
原始数列满足准光滑条件,且 ,生成数列满足准指数规律,可建立GM(1,1)模型。
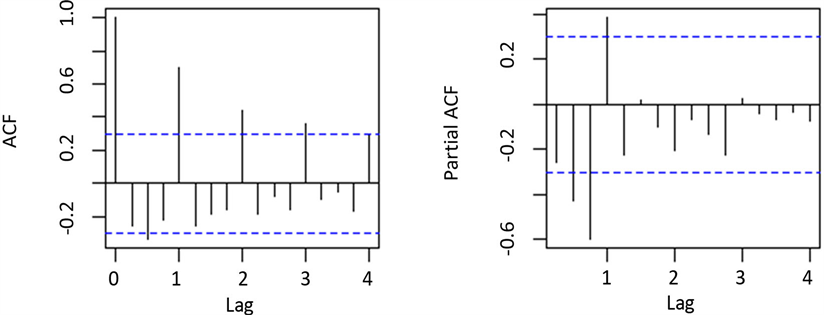
Figure 2. Two absolute difference autocorrelation diagrams and partial autocorrelation diagrams for differential income
图2. 两次差分收入绝对差自相关图和偏自相关图
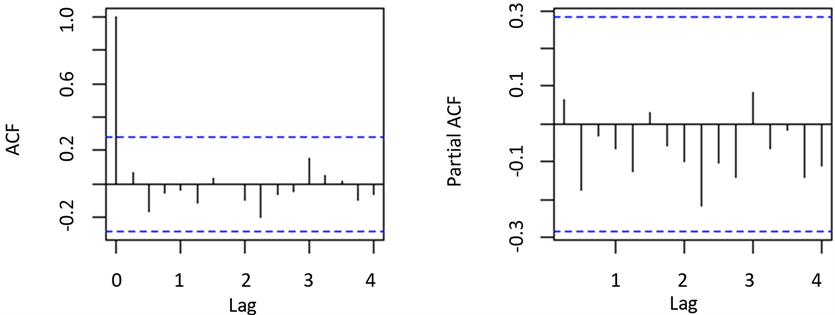
Figure 3. Autocorrelation diagrams and partial autocorrelation diagrams of model (7)
图3. 模型(7)残差自相关和偏自相关图
对一次累加数列建立微分方程 ,得到第一季度时间序列数据的时间响应函数为:
(8)
令 ,通过 即可得出第一季度城乡收入差距预测值。重复上述过程,分别求出第二季度、第三季度和第四季度预测值。
对建立的模型进行后验差检验,检验结果如表3所示。
从表3我们可以看出来四个季度的后验差比均C ≤ 0.35,精度P ≥ 0.95,都为一级精度,模型预测精度高,可用于外推预测。
3.4. ARIMA-GM组合模型的预测
根据组合模型权重求解方法,季节ARIMA模型所占权重 ,GM(1,1)模型所占权重 ,用湖南省2016年第一季度至2017年第三季度的城乡居民收入差绝对值数据,拟合模型季节乘法ARIMA模型、GM(1,1)模型及ARIMA-GM组合预测模型,计算模型的平均相对误差对三个模型的优劣进行评价,结果如表4所示。可以看出三个模型中,组合预测模型的平均相对误差最小,能够更精确地进行预测。
用同样的三种模型方法对湖南省城乡收入差比进行拟合,先建立季节乘法ARIMA模型和GM(1,1)模型,然后根据组合权重计算方法得出季节ARIMA模型所占权重 ,GM(1,1)模型所占权
Table 3. Test results of posterior difference
表3. 后验差检验结果
Table 4. Model evaluation results
表4. 三个模型评价结果
Table 5. Model evaluation results of income difference ratio
表5. 收入差比模型评价结果
Table 6. Forecast of urban-rural income disparity in Hunan province from 2018 to 2019
表6. 2018~2019年湖南省城乡收入差距预测
重 。同样用平均相对误差对三组模型进行模型评估,评估结果如表5所示。组合模型的拟合效果始终优于单个模型的拟合效果,可用于短期预测。
运用ARIMA-GM组合预测模型,对湖南省2018年至2019年的湖南省城乡居民收入绝对差以及收入差比进行预测,预测结果见表6。模型预测结果显示,到2019年第四季度,湖南省城乡收入绝对差预测累计达到23,829.403元,呈现持续不断扩大的趋势;相比之下,城乡收入差比保持在2.65左右,出现小幅增长,这说明相比过去,现在农村居民收入和城市居民收入都在以相同增速不断增长,这对于未来湖南省城乡一体化具有重要意义,但是形势依旧相当严峻。因此必须想办法提高农村居民收入,积极响应国家农村建设相关政策,缩小城乡收入差距,早日实现城乡一体化的奋斗目标。
4. 结论
季节乘法ARIMA模型能够识别数据中的长期趋势和季节趋势,对于非平稳数据也能够进行有效的处理,GM(1,1)模型能够在数据量较少、信息不充分的情况下做出有效的预测。ARIMA-GM组合模型结合两者的优势,即能较为准确的进行预测,通过组合权重又极大降低了预测误差,对于短期预测效果较好,可以用来对城乡收入差距做短期预测。
通过以上研究,我们可以得到湖南省未来两年的城市收入差距绝对值会继续增大,到2019年第四季度将累计增加到23,829.403元,而城乡收入差比呈现小幅上涨的态势,维持在2.65左右。说明尽管湖南省的城乡收入差距在不断逐渐缩小,但是形势依旧相当严峻,尤其湖南省农村人口众多。农村问题是十三五规划的一大重点问题,为此对城乡收入差距进行科学预测和分析,将成为政府制定相关政策的重要依据。本文构建的ARIMA-GM组合模型预测精度较高,可为政府制定城乡区域发展规划起到一定指导作用。
文章引用
屈文鑫,柳向东. 湖南省城乡居民收入差距预测—基于ARIMA-MA模型
Forecast of Income Gap between Urban and Rural Residents in Hunan Province—A Study Based on ARIMA-GM Combination Model[J]. 统计学与应用, 2018, 07(03): 330-339. https://doi.org/10.12677/SA.2018.73039
参考文献
- 1. 傅德红, 等. 我国城乡人均收入差距的实证分析和预测[J]. 社会视野, 2008(8).
- 2. Tu, X.L. (2011) Comparative Research on Prediction Model of China’s Urban-Rural Residents’ Income Gap. Asian Agricultural Research, 3, 88-91.
- 3. 辜子寅. 基于ARMA-GM组合模型的江苏省城乡收入差距预测[J]. 常熟理工学院学报, 2012, 26(8): 18-21.
- 4. 龚承刚, 王梦, 谢航. 基于ARIMA模型的湖北省城乡居民收入差距的预测[J]. 统计与决策, 2014(15): 94-97.
- 5. 汪潘义, 吴凤平. 灰色预测模型在季节波动预测中的应用[J]. 统计与决策, 2009(24): 22-23.
- 6. 李佩, 彭斯俊. 一种新的组合权重在组合预测模型中的应用[J]. 河南科技大学学报, 2018, 39(2): 87-98.
