Advances in Applied Mathematics
Vol.3 No.04(2014), Article
ID:14351,5
pages
DOI:10.12677/AAM.2014.34029
The Scaling Factor on the Sierpinski Gasket
Department of Applied Mathematics, Nanjing Audit University, Nanjing
Email: tdonglei@nau.edu.cn
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Aug. 24th, 2014; revised: Sep. 25th, 2014; accepted: Oct. 4th, 2014
ABSTRACT
In this paper, we give a statement of the computing method of scaling factor on the Sierpinski gasket. We will introduce two methods in computing the scaling factor under equal-weighted condition. One is by  Transformation. The other one is using extreme values in classical calculus theory.
Transformation. The other one is using extreme values in classical calculus theory.
Keywords:The Sierpinski Gasket, Scaling Factor, 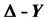 Transform
Transform

谢宾斯基垫片上的尺度因子
唐东磊,胡 锐,潘新月,孙亚萍
南京审计学院,应用数学系,南京
Email: tdonglei@nau.edu.cn
收稿日期:2014年8月24日;修回日期:2014年9月25日;录用日期:2014年10月4日

摘 要
本文将给出关于谢宾斯基垫片上尺度因子计算方法的综述。我们主要介绍等权条件下谢宾斯基垫片尺度因子的两种求法。一是用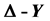 变换,另外一种则是用经典微积分中关于极值部分的理论。
变换,另外一种则是用经典微积分中关于极值部分的理论。
关键词
谢宾斯基垫片,尺度因子,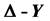 变换
变换

1. 引言
基于经典的微积分理论与泛函分析中的变分原理,Kigami ([1] -[3] )在有限分歧分形集合上用构造性的二阶差分法直接定义了拉普拉斯算子。在Kigami的理论框架下,我们还可以定义分形集合上的调和函数、狄利克雷形式与格林函数,给出调和函数的延拓公式。值得注意的是Kigami理论依赖于调和结构的存在性,而调和结构的存在性问题,仍然是当前分形分析领域中的一个非常重要的公开问题,尚待解决。关于分形集合上调和结构存在性的已有结果可参阅Lindstrøm [4] 。
在本文中我们将给出谢宾斯基垫片上调和结构的尺度因子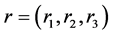 的存在性问题的综述。为了简便起见,我们假定对
的存在性问题的综述。为了简便起见,我们假定对 ,有
,有 ,仍然记为
,仍然记为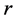 ,称之为谢宾斯基垫片上的尺度因子(参见Kigami [1] -[3] ,Strichartz [5] [6] )。
,称之为谢宾斯基垫片上的尺度因子(参见Kigami [1] -[3] ,Strichartz [5] [6] )。
谢宾斯基垫片[1] -[12] 由包含3个压缩映射的迭代函数系生成。其中压缩映射为
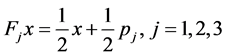 .
.
这里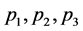 是平面上某个等边三角形的顶点。由Kigami理论知,谢宾斯基垫片的边界
是平面上某个等边三角形的顶点。由Kigami理论知,谢宾斯基垫片的边界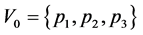 。
。
在经典的物理学中,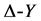 变换一般用来简化电路结构,研究等效电阻,常应用于谢宾斯基垫片上电阻网络的简化,可参阅文献[7] -[12] 。
变换一般用来简化电路结构,研究等效电阻,常应用于谢宾斯基垫片上电阻网络的简化,可参阅文献[7] -[12] 。
常用的计算分形集合上的尺度因子的方法有两种:一是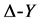 变换,可参见Strichartz [5] [6] ,Kigami [1] -[3] ;二是用应用一阶能量求偏导的方法,可参见Kigami [1] -[3] 。
变换,可参见Strichartz [5] [6] ,Kigami [1] -[3] ;二是用应用一阶能量求偏导的方法,可参见Kigami [1] -[3] 。
2. 谢宾斯基垫片上的尺度因子
在这一节我们将介绍两种计算尺度因子的方法。
2.1. 用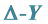 变换计算谢宾斯基垫片上的尺度因子
变换计算谢宾斯基垫片上的尺度因子
2.1.1. 等效互换的数学模型
等效互换的数学模型
在经典物理学的电路分析中,我们常常提到等效电阻。图1、图2分别是Y形和△形联接的电路,利用短接、断开方法将电阻Y形联接和△形联接变换为串、并联电阻组成的简单电路。根据等效电路的概念,

Figure 1. Y-type circuit
图1. Y形电路

Figure 2. △-type circuit
图2. △形电路
Y形联接的电阻与△形联接的电阻等效变换的条件是:1) 对应端流出的电流一一相等;2) 对应端之间的电压也一一相等;当满足条件(1) (2)后,在Y形与△形两种接法中,对应的任意两端间的电阻也必然相等。以上即为经典物理学中的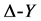 变换。为了得到
变换。为了得到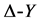 变换中等效电阻的计算公式,我们考虑图1和图2:
变换中等效电阻的计算公式,我们考虑图1和图2:
如图所示,图1是一个Y型联接的电阻模型,标注各个分界点(即顶点)为a、b、c、o,图2是一个△型联接的电阻模型,是图1经过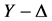 变换所得,根据等效电阻原理,其任意两点间的电阻值没变,现用R、r表示电阻,如
变换所得,根据等效电阻原理,其任意两点间的电阻值没变,现用R、r表示电阻,如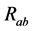 代表的是整个电路中a到b的电阻值,而
代表的是整个电路中a到b的电阻值,而 仅表示线段ab的电阻值,具体分析如下:
仅表示线段ab的电阻值,具体分析如下:
图1中,a、b之间的电阻是由电阻ao、ob经过串联所得,所以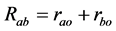 ,同理可得:
,同理可得: ,
,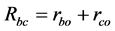 ;
;
图2中,顶点ab间的电阻是一个并联电阻,不仅仅包含了线段ab的电阻,还包含了从a点经c点到达b
点之间的电阻,由并联电阻相关求法可得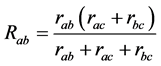 ,同理可知:
,同理可知: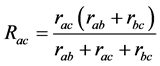 ,
, ;
;
再由等效电阻原理可得出三个等式:
 (1)
(1)
 (2)
(2)
 (3)
(3)
并联立(1)(2)(3),即求解一个三元一次方程组,可得到:
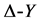 变换:
变换:
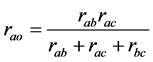 (4)
(4)
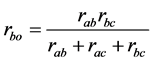 (5)
(5)
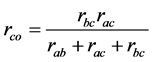 (6)
(6)
由(4)(5)(6)可知:特别地,如果令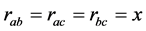 ,那么
,那么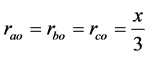 ;
;
同理可知,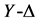 变换:
变换:
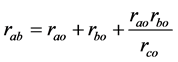 (7)
(7)
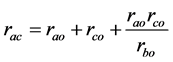 (8)
(8)
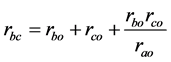 (9)
(9)
由(7)(8)(9)式可知:特别地,如果令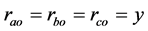 ,那么
,那么 。
。
2.1.2. 用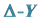 变换计算谢宾斯基垫片上的尺度因子
变换计算谢宾斯基垫片上的尺度因子
谢宾斯基垫片(可参阅[1] -[12] )
在图3中为了图形简便,我们直接用电阻线来表示电阻,同时为了计算方便,假定图3(a)中所有的电阻值均为1。图3(a)中顶点被红色圆点标记的电阻集由三个△形联接的电阻集组成,因此,我们可以用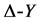 变换对(a)中三个△形联接的电阻集进行等效变换,得到图形如图3(b)所示,并利用(4)(5)(6)三个等式,计
变换对(a)中三个△形联接的电阻集进行等效变换,得到图形如图3(b)所示,并利用(4)(5)(6)三个等式,计
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e) (f)
(f)
Figure 3. △-Y transformation in the Sierpinski gasket
图3. 谢宾斯基垫片上的△-Y变换
算得到各边对应电阻值;(b)中所显示的是三个串联的电阻,由串联的电阻电阻值可以直接相加,我们将图形进行进一步简化,就可以得到图3(c);此时又得到一个包含△形联接的电阻集,再一次对其使用 变换得到图3(d);将(d)中的三个串联的电阻简化,就可以得到如图3(e)的Y型电阻;最后对(e)中Y型电阻使用
变换得到图3(d);将(d)中的三个串联的电阻简化,就可以得到如图3(e)的Y型电阻;最后对(e)中Y型电阻使用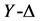 变换,并应用(7)(8)(9)三个等式,计算得到一个每个电阻都是5/3的△形联接的电阻集。由Kigami理论我们可以得到,在等权的情况下,谢宾斯基垫片上的尺度因子为3/5。
变换,并应用(7)(8)(9)三个等式,计算得到一个每个电阻都是5/3的△形联接的电阻集。由Kigami理论我们可以得到,在等权的情况下,谢宾斯基垫片上的尺度因子为3/5。
2.2. 用一阶能量求偏导的方法计算谢宾斯基垫片上的尺度因子
基于以上对谢宾斯基垫片的分析,以下采用一阶能量求偏导的方法来计算其尺度因子,具体方法如下:
如图4(a)所示,谢宾斯基垫片上3个顶点分别为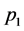 、
、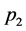 、
、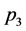 ,对应的中点为
,对应的中点为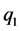 、
、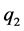 、
、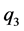 ,设
,设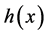 为定义在谢宾斯基垫片上的调和函数,图4(b)上所示为
为定义在谢宾斯基垫片上的调和函数,图4(b)上所示为 在以上各点的取值,假设
在以上各点的取值,假设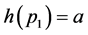 、
、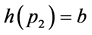 、
、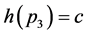 ,
, 、
、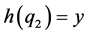 与
与 。则初始能量与第一层能量分别为
。则初始能量与第一层能量分别为
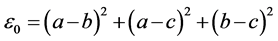
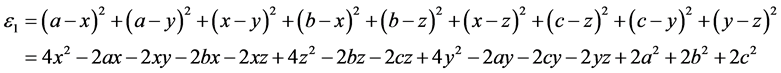
我们想要确定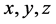 的值,从而使第一层能量最小化。根据经典的微积分理论,多元可微函数的极值点必定是其驻点。因此,现对其进行一阶能量
的值,从而使第一层能量最小化。根据经典的微积分理论,多元可微函数的极值点必定是其驻点。因此,现对其进行一阶能量 关于变量x、y、z求偏导令其等于0,可得如下方程:
关于变量x、y、z求偏导令其等于0,可得如下方程:
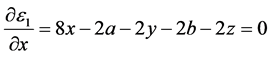 (10)
(10)
 (11)
(11)
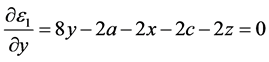 (12)
(12)
联立(10)(11)(12)式,分别求出x、y、z,结果如下:
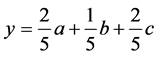 (a)
(a) (b)
(b)
Figure 4. Values of harmonic function on vertices of level 1 on the Sierpinski gasket
图4. 谢宾斯基垫片上调和函数在第一层各顶点处的值
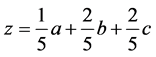
将x、y、z的值代入到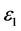 ,整理可得:
,整理可得:
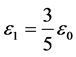
由Kigami理论即知,谢宾斯基垫片上的尺度因子为3/5。
3. 结论
本文介绍了两种计算谢宾斯基垫片上尺度因子的方法,注意到谢宾斯基垫片是有限分歧分形集合的一个典型例子,其尺度因子的计算方法可以推广到一般的有限分歧分形集合,可参见孙亚萍[11] 、潘新月[12] 等。第一种计算尺度因子的方法 变换的优点在于方便简捷,甚至可以计算非等权条件下分形集合上的尺度因子,但是其只适用于边界为3个顶点的分形集合的尺度因子求解问题;而第二种方法的优点在于可适用于更一般的有限分歧分形集合,应用前景更广泛,缺点在于计算较为繁琐。
变换的优点在于方便简捷,甚至可以计算非等权条件下分形集合上的尺度因子,但是其只适用于边界为3个顶点的分形集合的尺度因子求解问题;而第二种方法的优点在于可适用于更一般的有限分歧分形集合,应用前景更广泛,缺点在于计算较为繁琐。
致 谢
感谢评审专家对论文提出的宝贵意见。
基金项目
江苏省高校自然科学基金项目(12KJB110008)、江苏省青蓝工程项目、教育部留学归国人员科研启动基金项目(第45批)资助。
参考文献 (References)
- [1] Kigami, J. (1989) A harmonic calculus on the Sierpinski spaces. Japan Journal of Applied Mathematics, 8, 259-290.
- [2] Kigami, J. (1993) Harmonic calculus on p.c.f. self-similar sets. Transactions of American Mathematical Society, 335, 721-755.
- [3] Kigami, J. (2001) Analysis on fractals. Cambridge University Press, Cambridge.
- [4] Lindstrøm, T. (1990) Brownian motion on nested fractal. Memory of American Mathematical Society, 420.
- [5] Strichartz, R.S. (2000) Taylor approximations on Sierpinski gasket type fractals. Journal of Functional Analysis, 174, 76-127.
- [6] Strichartz, R.S. (2006) Differential equations on fractals: A tutorial. Princeton University press, Princeton.
- [7] 张永照, 杨万明, 张淑艳 (1995) 电阻形联接与形联接等效变换的简单推导. 大学物理, 3, 18-19.
- [8] 过祥龙, 张毓麟 (1997) Sierpinski电阻网络等效电阻的研究. 大学物理, 4, 8-10.
- [9] 郭慧丽 (2001) Sierpinski变形电阻网络等效阻值的研究. 甘肃高师学报, 2, 27-28.
- [10] 李建新 (2005) 一类n级嵌套的三角形电阻网络的研究. 安阳工学院学报, 13, 58-60.
- [11] 孙亚萍 (2011) Δ-Y变换在数学中的应用. 硕士论文, 南京审计学院, 南京.
- [12] 潘新月 (2013) 谢宾斯基垫片上尺度因子的求法. 硕士论文, 南京审计学院, 南京.