Advances in Applied Mathematics
Vol.04 No.04(2015), Article ID:16368,8
pages
10.12677/AAM.2015.44044
Prime Factorization of Sperner Theory
Taiyou Zhang1, Fugang Chao1, Han Ren1,2
1Department of Mathematics, East China Normal University, Shanghai
2Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, Shanghai
Received: Oct. 28th, 2015; accepted: Nov. 13th, 2015; published: Nov. 19th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Sperner theory is one of the most marvelous branches in extremal set theory. It has many applications in the field of operation research, computer science, hypergraph theory and so on. The original Sperner theorem is brilliant; however, there are quite a few constraints. Using number theory method, an alternative proof of Sperner theorem was obtained. As an application, we correspond subsets of Sperner to the roots of indefinite equations, simplifying the complex conformation of the set of solutions and getting nicer properties. The utilization of symmetric chain decomposition plays a great role in promotion, by establishing numerical correspondence between symmetric chain structure and integer collection. The symmetric chain decomposition method also supports the promotion. We build a connection between chains and collections.
Keywords:Sperner Theory, Generating Function Method, Symmetric Chain

Sperner理论的质因子分解问题
张泰滺1,晁福刚1,任韩1,2
1华东师范大学数学系,上海
2上海市核心数学与实践重点实验室,上海

收稿日期:2015年10月28日;录用日期:2015年11月13日;发布日期:2015年11月19日

摘 要
Sperner理论是建立在偏序集上的极值理论,在运筹学、计算机、超图理论等领域有很多的应用。然而原始的Sperner定理对集合限制颇大。本文的主要工作是借助于数论的方法,给出Sperner定理在自然数域上推广的一个可选择的证明。将Sperner中集合与不定方程的解对应起来,把复杂的集合结构简化为解的结构,得到了良好的性质。推广中还运用对称链分解辅助说明,凭借架构对称链数量上的一一对应,证明了推广的部分。
关键词 :Sperner定理,生成函数,对称链

1. 引言
Sperner理论在极值组合论的众多领域中占有一席之地,是组合数学中的一个有深远影响的研究方向,这一理论偏向于研究建立在偏序集、偏序关系上的极值可能性以及范围。由于偏序集的包容性使其延伸广泛,很有深度,因此在许多领域都被广泛地应用。从二十世纪二十年代左右开始渐渐发展成为一个独立课题。大约三十年代以来,由于同超图理论相互映证,得到了快速的的发展。
谈到此理论的发源,就要从上个世纪Sperner做出的一个看似朴素但又是前所未有的成果,即对于子集格来说,基数最大的反链是由秩最大的集合组成的。按集合论观点来说就是研究离散数学中在偏序集上中相互不存在比较关系的元素的最大集合。
Sperner理论[1] 问世是一个里程碑。许多伟大的数学家,如Dilworth [2] ,Katona [3] ,Kleitman [4] 等,都对这类问题有极大的兴趣,经过了大量的研究和猜想,在Sperner原理论基础上做出了许多经典的结果,使得该理论有了很大的进展。Bruijin,Tengbergen和Kruyswiji [5] 于1949年给出了把单纯建立在集合包含关系上的Sperner性质推广到分拆因子格证明。而Erdös、Ko和Rado [6] 在1961年进行大规模的推演后获得了关于交反链的Erdös-Ko-Rado定理——当下被称为Sperner理论体系最漂亮的成果之一。涉及了Erdös-Ko-Rado定理的模拟、推广及应用文献如雨后春笋般出现,极大推动了该领域的进步 [7] 。而后Lih [8] 于上世纪八十年代给出了Sperner定理限定在子集上的形式。
除代数方法之外,对这些问题的研究过程中引入了几何、概率、线性规划等数学分支进来,产生了很多独特的想法和技巧,从而形成Sperner理论。这门学科在不断地推广下渐渐形成一门独立的分支学科,同时该理论体系不仅同许多数学领域关系密切,诸如概率论、数论、超图理论等等,其在计算机领域的应用也十分广泛,在计算机理论、编码纠错原理,以及概率论等等方面具有很大的价值。
在众多关于偏序集研究的成果中,比较有价值或者说较为深刻的是对包含关系下的n元子集格的研究。超图领域与该理论体系的关联是一个重要发现,这一点直接导致大量前者的术语经常被用来描述以子集格为研究对象的极值结果。除此之外大量漂亮的结论推广到了以整除关系为偏序关系的整数分拆格上,本文中主要讲述的就是建立在整除关系上,关于整数质因子分解的极值问题。
2. 基本概念以及符号说明
本文的研究对象是建立在整数的质因子分解的因子集合,主要分析集合与集合之间的关系并构建数学联系,在这研究过程中需要运用一系列集合尤其是偏序集的概念诸如偏序关系、阶、比较、覆盖等等概念,定义如下:
对于非空有限集合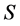 定义一种关系
定义一种关系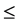 ,如果满足以下三条:
,如果满足以下三条:
1) 对于任意的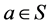 ,则
,则 ;
;
2) 对于任意的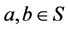 ,若
,若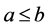 且
且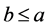 ,那么
,那么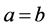 ;
;
3) 对于任意的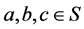 ,若
,若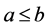 且
且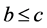 ,那么
,那么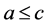 。则称
。则称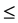 是一种定义在
是一种定义在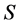 上的序关系,这时称集合
上的序关系,这时称集合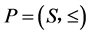 为一个偏序集。
为一个偏序集。
如果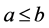 或者
或者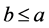 ,则称
,则称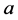 和
和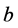 是可以比较的,否则称
是可以比较的,否则称 和
和 为不可比较的。如果
为不可比较的。如果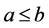 同时
同时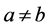 ,则记为
,则记为 。如果
。如果 且不存在
且不存在 使得
使得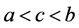 ,则称
,则称 覆盖
覆盖 。
。
有限集合 中,假如只存有唯一的元素
中,假如只存有唯一的元素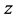 ,使得关于所有
,使得关于所有 ,满足
,满足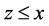 ,那么叫这类元素
,那么叫这类元素 为
为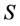 中的极小元;假如只存有的元素
中的极小元;假如只存有的元素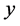 ,使得关于所有
,使得关于所有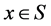 ,满足
,满足 ,这时叫这类元素
,这时叫这类元素 为集合
为集合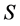 中的极大元。
中的极大元。
设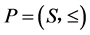 是偏序集,对于任意
是偏序集,对于任意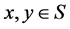 ,如果
,如果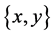 都可以取到上界中的下确界和下界中的上确界,那就能够称该集合集
都可以取到上界中的下确界和下界中的上确界,那就能够称该集合集 形成一个格。
形成一个格。
对于一个偏序集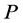 ,若存在函数
,若存在函数 ,使得:
,使得:
1) ,这里
,这里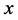 为
为 的极小元;
的极小元;
2)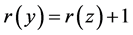 ,这里
,这里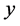 覆盖
覆盖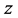 。
。
则称偏序集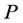 为分次偏序集,
为分次偏序集,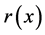 记为
记为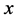 的阶,偏序集
的阶,偏序集 的阶定义为
的阶定义为 中元素阶的最大值。
中元素阶的最大值。
偏序集合,即配备了偏序关系的集合。序关系直观地说明了集合概念,表示出集合上元素之间的联系,诸如排序或排列等。使用交反链、对称链等一类关于链的概念在解决Sperner理论中的问题上往往有独到之处。
当谈到链一般有提到Dilworth定理,一个非常著名的定理:一个偏序集里,最小的链划分个数即是此中最长反链的长度。这个定理在组合极值体系中起到了不可或缺的作用。与此同时偏序结构在数学各分支中的应用广泛,这直接导致了链分解性质在拓扑、大数据等学科的研究中常扮演着重要的角色。下面对本文中涉及的链进行简要说明:
假如 的一个子集
的一个子集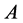 中的元素是互相之间不存在偏序关系,那么就说
中的元素是互相之间不存在偏序关系,那么就说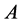 是
是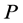 的一条反链。从集合包含关系额角度来说来说,设
的一条反链。从集合包含关系额角度来说来说,设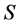 是一个
是一个 元集合,
元集合,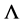 是
是 的一个子集族,如果对任意
的一个子集族,如果对任意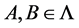 都有
都有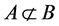 ,则称
,则称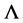 为反链。
为反链。
序集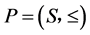 是具有阶函数
是具有阶函数 的分次偏序集,那么
的分次偏序集,那么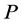 的元素
的元素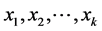 形成一条对称链,如果满足:
形成一条对称链,如果满足:
1)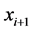 覆盖
覆盖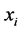 ,
, ;
;
2)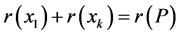 ,这里
,这里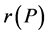 为
为 的最大阶。
的最大阶。
在对于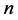 元集合
元集合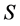 ,设
,设 为
为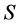 的子集,若满足:
的子集,若满足:
1)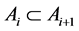 且
且 ,
, ;
;
2) 。
。
则称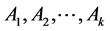 形成一条对称链。
形成一条对称链。
3. Sperner定理的因子分解形式
Sperner在1928年得到的结果被视作是这一理论体系的源头:
定理3.1 如果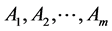 是
是 的一些子集,
的一些子集, 是S子集族,满足:任意
是S子集族,满足:任意 可得
可得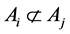 ,那么
,那么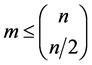 。
。
先作出如下定义,如果有一个n元排列中前 个元素都为
个元素都为 中的元素,那么就称这个排列是以
中的元素,那么就称这个排列是以 开头。显然,一种排列不可能同时以
开头。显然,一种排列不可能同时以 开头,否则必将会导致
开头,否则必将会导致 或者
或者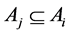 与条件矛盾,由此得知以互不包含的集合开头的排列是不相同的,这些排列的个数大于等于集合元素的个数。n元集合S的全排列共有n!种,而以
与条件矛盾,由此得知以互不包含的集合开头的排列是不相同的,这些排列的个数大于等于集合元素的个数。n元集合S的全排列共有n!种,而以 开头的排列数为
开头的排列数为 种,从而以满足上述条件的集合作为开头的排列总和为
种,从而以满足上述条件的集合作为开头的排列总和为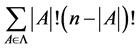 。可以得到
。可以得到
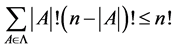
在这里假设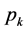 为子集族
为子集族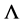 中k元子集的个数,那么
中k元子集的个数,那么
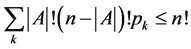
故有

作为Sperner定理结论的补充, 的模取到最大值当且仅当反链由模为
的模取到最大值当且仅当反链由模为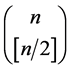 的子集或者模为
的子集或者模为 的子集组成。
的子集组成。
Sperner定理在集合论上具有极其深刻的影响力,在这里首先不妨将集合视作元素,包含关系视作偏序集,在这样认知下该定理对于其他形式的偏序集上也有很大的价值。通过转化几个偏序的概念,可以得到以下的推论:
推论 3.2 设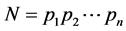 是自然数
是自然数 N的质因数分解,则N中两两无整除关系的因子所构成集合的全体中,单个集合所包含的元素个数最多为
N的质因数分解,则N中两两无整除关系的因子所构成集合的全体中,单个集合所包含的元素个数最多为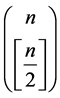 .
.
将数的整除关系看做原定理中集合的包含关系,一个个正因子对应到子集簇中的子集,而自然数N按作用则可等价看做Sperner定理中的S。从这些概念等价推导过来,结论是成立的。
N的任何一个因数都可以像这样表示成 ,
, 。于是一个因数
。于是一个因数 通过质因子分解
通过质因子分解
的下标对应于 中的一个子集
中的一个子集 ,因数和子集之间构成一一对应的关系,所以可以认为一组因数两两之间不存在整除关系等价于其对应的集合系是Sperner系,即该集合簇中集合两两之间不存在包含关系,至此等价关系证明完毕。
,因数和子集之间构成一一对应的关系,所以可以认为一组因数两两之间不存在整除关系等价于其对应的集合系是Sperner系,即该集合簇中集合两两之间不存在包含关系,至此等价关系证明完毕。
4. Sperner定理质因子分解形式的推广
在以上推论的描述中知道N的局限性很大,只有在满足N等于质数一次幂的乘积的时候,才能对上界进行限制,对于诸如“4”这样平凡的自然数却无能为力。本文接下来的工作就是设法把N的值域扩展到整个自然数域,换句话来说就是研究自然数N中两两无整除关系的因子所构成集合中元素最多能有多少?
为突破这个局限,首先尝试使用了生成函数法:在研究离散数列的性质时,把其中一部分特性同化到幂级数里,借助幂级数这类运算的种种良好的性质确定离散数列的结构。在这里生成函数非常巧妙地把正因子的次数和方程组的解相联系,凭此找到了可能的突破口。
设 ,
,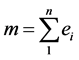 ,其因数对应到每个质因子的幂次受到
,其因数对应到每个质因子的幂次受到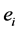 的控制,通俗来说对于N的一个正因数都要考虑该因子中包含多少个
的控制,通俗来说对于N的一个正因数都要考虑该因子中包含多少个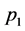 ,包含多少个
,包含多少个 ,…,直到包含多少个
,…,直到包含多少个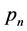 。
。
取N中任意一个因数 为例,有
为例,有
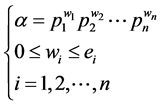
定义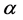 的次数为
的次数为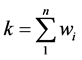 。
。
上面的不定方程描述了N每个因子的特点,然而还不够清楚明了,还可以通过进一步的演化来抓住因子的主要特点。对于N的k次因数的个数可以借助生成函数法的思想,观察下式中k次幂系数:

依次从括号中提取出一个质因子的幂次,合并得到不定方程:

到目前为止,已经把原问题:求N中相互没有整除关系的因子集合的规模,转变成考虑不定方程解的个数。虽然从上面的推导已知一个因子可以转化成一个不定方程的解,还是要对这种方法的合理性进行验证,不定方程的解是否严格与N中因子一一对应。
引理4.1 上述方程任意两个解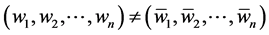 ,这两个解对应的N的k次因数
,这两个解对应的N的k次因数 与
与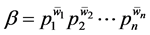 之间不存在相互整除关系。
之间不存在相互整除关系。
由于 和
和 结构上几乎一致,那在证明中不妨令
结构上几乎一致,那在证明中不妨令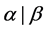 。如果
。如果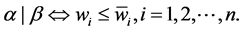 根据生成函数法的推导,有
根据生成函数法的推导,有 ,
, ,由算术基本定理知,同时满足这两个条件只有一种可能,即
,由算术基本定理知,同时满足这两个条件只有一种可能,即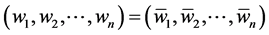 。这说明
。这说明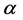 和
和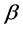 是N的同一个因子,这与条件矛盾。
是N的同一个因子,这与条件矛盾。
完成了因子与不定方程的解一一对应的证明,现在可以得到:
定理4.2 N所有k次两两无整除关系的正因子的集合的最大规模等于不定方程

的非负整数解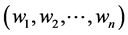 的个数。
的个数。
如记N的次数是k的所有因数的集合为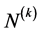 。
。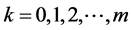 ,
,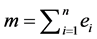 ,则
,则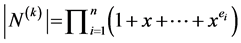 中
中 的系数。结合引理4.1知,定理4.2成立。
的系数。结合引理4.1知,定理4.2成立。
从这个定理开始,就可以通过分析这个不定方程解的结构来描述N的互不整除的因子数。不得不说,这个不定方程解的结构还是有非常漂亮性质的:
性质4.3 N所有k次两两无整除关系的正因子的集合的最大规模等于N所有 次两两无整除关系的正因子的集合的最大规模。
次两两无整除关系的正因子的集合的最大规模。
方程组解的个数具有等距离对称的性质:第一个等式等于k和等于 拥有一样多的解。对于方程组中第一个方程进行变形,用
拥有一样多的解。对于方程组中第一个方程进行变形,用 去减掉左边的
去减掉左边的 可以得到:
可以得到:
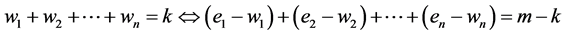
很明显两边方程的解的个数相等,通过等价关系于是两个正因子集合的元素数目一致。
通过这个性质把需要考虑情况减去一半,接下来只要研究剩下一半中解的情况。该解的结构具有单峰性。
在展开对称链方法之前,首先重述一遍推广的意图以理清思路:Sperner定理在质因子分解上的应用存在较大的局限,它无法作用于任意自然数而是仅仅作用于可以由互异单个质因子乘积得到的自然数。为了较清晰地展示对称链法,先对以下符号做出说明:
这里引入任意的自然数的标准分解式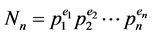 ,
, 为素数,
为素数,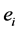 为自然数,下缀的n代表共有多少种质因子。
为自然数,下缀的n代表共有多少种质因子。
同样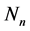 的任意一个因数的标准分解式
的任意一个因数的标准分解式 ,
,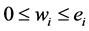 ,
, ,这里
,这里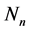 和
和 的次数分别定义为:
的次数分别定义为:

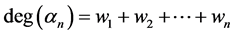
记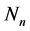 中组成一条对称链的因数序列为
中组成一条对称链的因数序列为 ,
, 。其中
。其中 表示
表示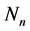 的正因数集合。
的正因数集合。
在确定了符号标记后,便可以展开对称链法。对称链法的大体思路是把集合中的对称链与集合中元素构建数学关系,从而通过对称链的数量限制集合中元素的数量,当然这种方法是有前提的。
引理4.4 (自然数因数集的对称链分解定理)自然数 的因数集
的因数集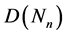 可分解为一组不相交的对称链之并。
可分解为一组不相交的对称链之并。
证明:使用递推的方法进行验证。当n=1时, ,这时有且仅有一条对称链
,这时有且仅有一条对称链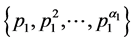 ,此时定理结论成立。
,此时定理结论成立。
当n = k时,设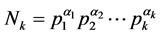 ,这时令
,这时令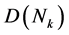 可以分解为一组不相交的对称链之并,观察n = k + 1的情况,有关系式
可以分解为一组不相交的对称链之并,观察n = k + 1的情况,有关系式 ,从
,从 的不相交对称链之并中取出一条形如
的不相交对称链之并中取出一条形如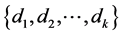 的对称链。需要注意的是这里的证明对称链的形状并无特殊要求,其他
的对称链。需要注意的是这里的证明对称链的形状并无特殊要求,其他 中对称链也可以通过相同的方法来构造成为
中对称链也可以通过相同的方法来构造成为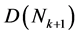 中不相交的对称链。
中不相交的对称链。
对于 按照如下方法进行构造:
按照如下方法进行构造:

构造法中t的作用是使每个序列都构成对称链。
显然上面的序列成功将一条对称链构造成n = k + 1时的对称链,从形状上来看构造的非常成功,两两之间不相交。但还需要进一步的分析来应证来确定该构造法的确达到了期望的地步,需要解决两个合理性问题:两条不同的对称链是否会构造出相同重复的一条新对称链;是否每一个因子都可以在某一条新构造出的对称链中找到。
定理4.5 任意两条 中的对称链构造出的n = k + 1时的对称链相互无交。
中的对称链构造出的n = k + 1时的对称链相互无交。
从 中任意取出两条互不相交的对称链,分别为
中任意取出两条互不相交的对称链,分别为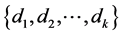 ,
,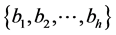
已知自然数的标准分解式为:
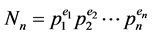 ,
, ,
,
其中e代表 的次数,r为阶函数。
的次数,r为阶函数。
那么这两条对称链中的元素的阶函数满足:
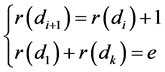
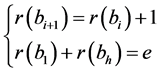
任意分别在对称链中取出两个元素,并通过上文关于对称链的构造法,变成新对称链中元素,形如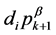 和
和 。
。
用反证法:如果要求这两个元素相等,等价于原来取出的元素相等且关于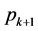 的指数相等,即
的指数相等,即

由于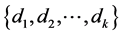 ,
, 是两条彼此之间无公共元素的对称链,故di≠bi 得出假设矛盾。
是两条彼此之间无公共元素的对称链,故di≠bi 得出假设矛盾。
定理4.6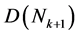 中每个元素都属于从由
中每个元素都属于从由 中对称链构造出的新对称链。
中对称链构造出的新对称链。
任意一个 中的元素必可以表示为
中的元素必可以表示为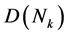 中某元素,记为M,与
中某元素,记为M,与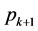 幂次的乘积,而已知M必然在
幂次的乘积,而已知M必然在 一条对称链中,由引理3中所述构造法可知,任意
一条对称链中,由引理3中所述构造法可知,任意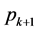 幂次与M的乘积都会包含在新的对称链里面,故定理得证。
幂次与M的乘积都会包含在新的对称链里面,故定理得证。
综上,完成了对于构造法合理的验证,从而得到了自然数因数集的对称链分解定理。这个定理说明自然数因数集拥有对称链分解的性质,从而可以用这个性质引出Sperner定理的推广:
定理4.7 对于任意自然数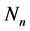 ,其质因子分解式表示为
,其质因子分解式表示为 ,如果记
,如果记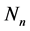 的所有次数是k的因数全体为
的所有次数是k的因数全体为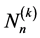 ,
,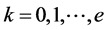 ,
,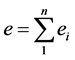 ,则
,则 的两两之间不存在整除关系的正因数集合的最大规模为
的两两之间不存在整除关系的正因数集合的最大规模为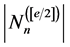 ,即次数为
,即次数为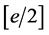 的所有因子的规模。
的所有因子的规模。
把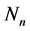 的所有因数
的所有因数 分拆成一组不相交的对称链,记为
分拆成一组不相交的对称链,记为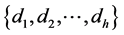 。而这其中的每条对称链一定至少含有一个次数为
。而这其中的每条对称链一定至少含有一个次数为 的因数。否则,根据对称链的定义可以知道任取同一条对称链中的对应的两个元素的阶函数的和必然等于
的因数。否则,根据对称链的定义可以知道任取同一条对称链中的对应的两个元素的阶函数的和必然等于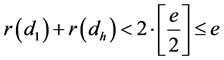 ,这与对称链定义矛盾。与此同时
,这与对称链定义矛盾。与此同时 的两两之间不存在整除关系的正因数集合即是取其中的反链,一条反链在每条对称链中最多取一个元素,故反链最大规模为
的两两之间不存在整除关系的正因数集合即是取其中的反链,一条反链在每条对称链中最多取一个元素,故反链最大规模为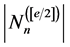 ,所以通过等价关系可以得知:
,所以通过等价关系可以得知: 的两两之间不存在整除关系的正因数集合的最大规模为
的两两之间不存在整除关系的正因数集合的最大规模为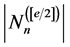 ,即次数为
,即次数为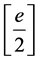 的所有因子的规模。证毕。
的所有因子的规模。证毕。
5. Sperner定理的实际应用
在完成了定理的纯理论的解释和证明之后,下面补充了应用定理的一个简单例子,在这个例子可以发现生成函数的优越性。设有自然数 ,计算
,计算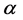 的两两之间不存在整除关系的正因数集合的最大规模。
的两两之间不存在整除关系的正因数集合的最大规模。
按照定理,所要求的数目就是 。由生成函数法转化为:
。由生成函数法转化为:
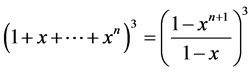
只需计算式子中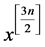 的系数。作分类讨论,当n = 2m时,所求数目为
的系数。作分类讨论,当n = 2m时,所求数目为 。此时满足:
。此时满足:
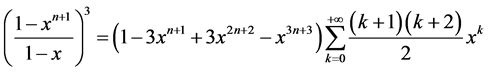
其中 的系数为
的系数为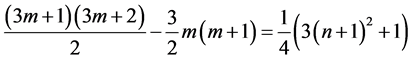 ,故
,故 为
为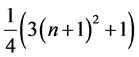 。当
。当 时同理可得,
时同理可得,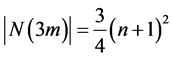 。
。
综上所述, 。
。
基金项目
本文得到国家自然科学基金(数学基地科研训练及能力提高)项目资助和上海市科学技术委员会的资助,资助课题编号为13dz2260400。
文章引用
张泰滺,晁福刚,任韩. Sperner理论的质因子分解问题
Prime Factorization of Sperner Theory[J]. 应用数学进展, 2015, 04(04): 357-364. http://dx.doi.org/10.12677/AAM.2015.44044
参考文献 (References)
- 1. Sperner, E. (1928) Ein Satz über Untermengen einer endlichen menge. Mathematische Zeitschrift, 27, 544-548. http://dx.doi.org/10.1007/BF01171114
- 2. Dilworth, R.P. (1950) A Decomposition Theorem for Partially Or-dered Sets. Annals of Mathematics, 51, 161-166. http://dx.doi.org/10.2307/1969503
- 3. Katona, G. (1975) Extremal Problems for Hypergraphs. In: Hall Jr., M. and van Lint, J.H., Eds., Combinatorics. http://dx.doi.org/10.1007/978-94-010-1826-5_11
- 4. Kleitman, D.J. and Sperner, J. (1973) Families of k-Independent Sets. Discrete mathematics, 6, 255-262. http://dx.doi.org/10.1016/0012-365X(73)90098-8
- 5. de Bruijn, N.G., van Ebbenhorst Tengbergen, C. and Kruyswijk, D. (1949) On the Set of Divisors of a Number. Nieuw Archief voor Wiskunde, 23, 191-193.
- 6. Erdös, P., Ko, C. and Rado, R. (1961) Extremal Problems among Subsets of a Set. Quarterly Journal of Mathematics Oxford Se-ries, 12, 313-318.
- 7. Greene, C., Katona, G. and Kleitman, D.J. (1976) Extensions of the EKR Theorem. Studies in Applied Mathematics, 55, 1-8. http://dx.doi.org/10.1002/sapm19765511
- 8. Lih, K.W. (1987) Problems in Finite Extremal Set Theory. Surikaisekikenkyusho-Kokyuroku, 607, 1-4.