Advances in Applied Mathematics
Vol.05 No.01(2016), Article ID:16976,6
pages
10.12677/AAM.2016.51007
On the Assigning Problem in Operation Research
Tianxiao Zhao1, Fugang Chao2, Han Ren2,3
1Department of Mathematical Science, Tsinghua University, Beijing
2Department of Mathematics, East China Normal University, Shanghai
3Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, Shanghai

Received: Jan. 29th, 2016; accepted: Feb. 21st, 2016; published: Feb. 24th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we characterize the assigning problem and present an algorithm to compute the optimal solutions efficiently. In our everyday life, such problems are always needed to use assigning methods to give a good solution. Since they are 0-1 problem, we may find relative optimal solutions.
Keywords:Operation Research, Assigning Problem, Simplicial Algorithm

运筹学中的指派问题
赵天骁1,晁福刚2,任韩2,3
1清华大学数学科学系,北京
2华东师范大学数学系,上海
3上海市核心数学与实践重点实验室,上海

收稿日期:2016年1月29日;录用日期:2016年2月21日;发布日期:2016年2月24日

摘 要
详细给出指派问题的定性刻化,同时提供一个可行算法,有效计算指派问题的最优解。在日常生活中会遇到类似的问题,需要用指派问题进行解决,使得完成任务的总效率最高,就需要用指派问题进行解决。由于是0-1问题,所以总能求的相对最优解。
关键词 :运筹学,指派问题,单纯形算法

1. 背景与数学模型
在日常生活中常遇到这样的问题:某单位需要完成项任务,恰好有个人可以承担这些任务。由于每个人专长不同,各人完成任务的效率也不相同。于是产生了这样一个问题:指派哪个人去完成哪些任务,使得完成项任务的总效率最高?这类问题称为指派问题(Assigning problem)。指派问题在博弈论与经济行为[1] 、和生态经济学 [2] 等学科都有广泛的应用,文中未加说明的符号和术语参见文献 [3] 。
如果用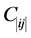 表示i个人完成第j项工作的效率,
表示i个人完成第j项工作的效率,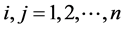 ,而变量
,而变量
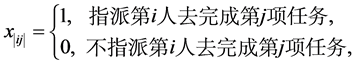
则相应的极小化数学模型为
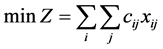 , (1)
, (1)
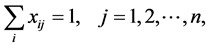 (2)
(2)
 (3)
(3)
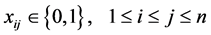 (4)
(4)
由上所述,指派问题有以下几个特点:
1) 指派问题是一个平衡的0-1运输规划问题。这可以由(2)~(4)看出。
从上讲,可以用表上作业法或单纯形法救解。但,当阶为较大时这些方法过于繁琐。可以利用其自身特点建立更为简单有效的方法。
2) 代数性质。不难由(2)~(4)看出,每一次指派对应于一个n阶排列。如果将(xij)视为一个n × n指派方阵,则(2),(3)表明:每次指派对应于n个位于不同行不同列上1的定位。故,所有可能方法数为n!。由此可见,指派问题一定有最优解。但是,用穷法来决定最优解其工作量是巨大的。这可以由Stirling公式
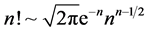
看出。
3) 最优指派的不变性。
指派问题的最优解有这样的一个重要特性:如果从系数矩阵(Cij)的一行(列)各个元素中分别减去一个常数c (通常是该行或列的最小元素),得到一个新的矩阵(bij)。那么以(bij)为系数矩阵求得的最优指派和原系数矩阵的最优指派相同。
值得注意的是,对于这个性质进行证明对于理解它是必要的。现在提供一个简短的证明如下:
设原问题的最优指派为
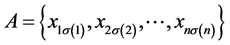 ,
,
其中,
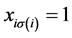 ,
,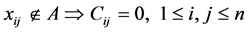 ,
,
且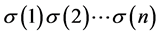 是1到n的一个排列。易见,相应的最优值为
是1到n的一个排列。易见,相应的最优值为
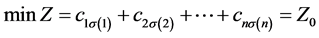
不妨设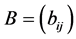 是将
是将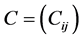 的第一行各元素减去c后得到的新矩阵。则B所对应指派问题在A上的值为。
的第一行各元素减去c后得到的新矩阵。则B所对应指派问题在A上的值为。
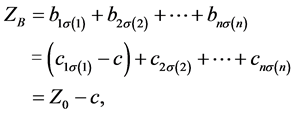
所以,
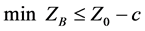 。
。
另一方面,设B在某指派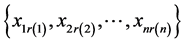 上达到最小,即有
上达到最小,即有
 。
。
故,
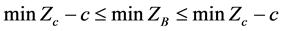
从而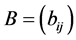 在指派
在指派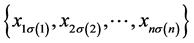 上的值
上的值 最小。
最小。
关于此性质有以下几点应说明如下:
1)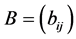 与
与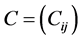 的最优指派相同是指它们的最优解集合完全一样,但它们的目标函数的量优值不一定相同。除非B = C。
的最优指派相同是指它们的最优解集合完全一样,但它们的目标函数的量优值不一定相同。除非B = C。
2) 这个性质提供了这样一种途径:在保留最优指派集合不变前提下,通过相应的行列变换,将原系数矩阵化为一个含有充分多0元素的矩阵,其指派问题最优解易于决定。
2. 指派的决定
指派的决定十分重要。如果当前矩阵中独立0元素(位于不同行列不同列的0元素)个数为阶数n时,指派问题已经解决;当独立0元素个数小于n时,由Konig定理可知,必须将这个系数矩阵进一步化简,以便有更多的独立0元素出现。因此每次指派都起着承前启后的作用。
指派的决定包含两个阶段:首先进行试指派,然后根据性质3和匈牙利方法进行调节。其算法如下:
Step 1. 利用性质3将原矩阵各行(列)减去响应行(列)的最小元素,直到新系数矩阵每行每列均有0出现。
Step 2. (救极大独立0元素集合。如果阶数较小,可以用直观法得到。否则,按以下步骤进行)
从0元素最少的行(列)开始,比较这一行各0元素所在列中0元素数目。选择0元素最少的那一列所对应0元素为一个独立0元素,然后划去同行同列其它0元素,直到所有0元素都被化去或被选定为0元素。如果独立0元素数目等于阶数n,则最优指派已求出;否则执行下一步。
Step 3. (求最大独立0元素集合)
求出一对非独立0元素01和02,它们之间有一条交错链(独立0元素和非独立0元素交替出现)相连,而且这条交错链不可扩张成更长的交错链,则将链上的非独立0元素与链外独立0元素合并成一个更大的独立0元素集合。重复这一过程直到这样的可扩交错链不存在。(此时的独立0元素集合具有最多元)。
Step 4. 用匈牙利方法求得若干条直线覆盖所有0元素(直线数目 = 前一步求出极大独立0元素数目)。
Step 5. (寻求新的0元素)
在没有被直线覆盖的元素中求最小元素,然后在所有未被直线覆盖的行中各元素减去这个最小元素,同时在被竖直的直线覆盖各元素中加上这个最小元素(以保留相应列中独立0元素不变)。转Step 2。
关于这个算法有以下几点须说明如下:
1) 适用于极大独立0元素集合。
Step2求出的独立0元素集合不一定是最大的,但一定是极大的。(清华版《运筹学》 [4] 第132页亦未提供最大性的证明)。此处Step 3将其调节为最大的独立0元素集合。其理论基础是图论中匹配的交错路理论 [1] 。这因为匈牙利方法求出的覆盖0元素的直线数恰好求出等于当前的最大独立0元素数目。这一点可以由操作过程得出。
2) Step2可以简化。只用求用一个极大0元素集合替代,虽然Step2提供的方法过于繁琐。
3) 用Step4得出的新矩阵中0元素数目不一定比原来的矩阵的少(并非如清华版《运筹学》第131~132页强调的那样“0元素严格增加”)。
因为虽然在未被直线覆盖的元素中减去最小元素可增加其中的0元素,但在相应的竖直直线覆盖的元素中加上这个最小元保留却可能减少更多的0元素。但是,有一个重要的信息却保留下来了,即:新矩阵有一个极大独立0元素集合包含了当前直线所覆盖的极大独立0元素集合。表明新矩阵中极大独立0元素数不小于原矩阵的当前极大独立–元数目。这一点可以由下例中看出,在这里新矩阵是由原矩阵经过上述运算得到的。

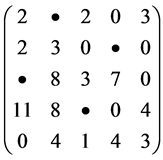
左边矩阵含有11个0元而右边的含有10个0元,但是前者中独立0元素却在后者中保留下来。这里,·表示独立0元素。
4) 匈牙利方法求出竖直直线数目一定少于未被直线覆盖的元素形成矩阵的行数。这一点可由求直线的过程看出。
5) 总效率严格递减。
由性质(3)可以知道,原矩阵的行上减去的元素总和大于列上减去元素的总和,意即:新矩阵效率总和严格小于原矩阵效率总和。正是由于这个性质使得该算法执行至多a次后停止。这里,a是初始系数矩阵的总效率。
6) 本算法适用于最大化的指派问题。只要注意到此算法仅利用了效率系数均非负或均非正这个特性。将目标函数反号,同时所有效率系数反号,然后执行该算法求最小指派既可。
3. 应用
例1 求以下所示效率矩阵的指派问题的最小解。

解:第1行到第5行的最小元素分别为7,6,7,6,4。按照Step 1,各行分别减去各自的最小元素后得到一个各行各列均含0元素的矩阵
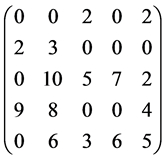
执行Step 2和Step 3选定一组最大的独立0元素(用实心的黑色圆·表示),有
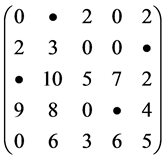
因为:独立0元素数目 = 4 (<5),必须执行Step 4以求4条直线覆盖所有0元素。这4条直线分别位于第1,2,4行和第1列,而未被覆盖的元素位于第3和第5行。其中最小元素是2。执行Step5后得到矩阵
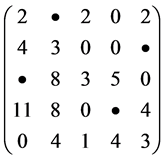
可以看出,执行Step 5后并未增加0元素。返回Step2求得一组最大独立0元素集合中实习黑圆所示):
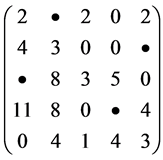
其中独立0元素个数5 = 阶数。最优指派已经决定,既:

例2 计算以下赋权完全二部图的最小完美匹配。其中边(Xi, Yj)权为矩阵中(i, j)处的值(如以下右边两个图所示)。
解:经过Step 2和Step 3选定独立0元素如中间上图所示,而下图对应于相应的匹配。经过Step 4和Step5求得新矩阵(所含0元素并未增加),重新返回Step 2和Step 3选定最大独立0元素集合如右边上图所示,下边对应于相应的完美匹配。
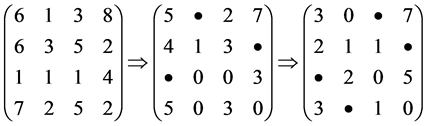
其最小匹配值为
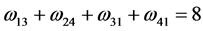
(注:利用该算法亦能计算赋权完全二部图上的最大匹配)。
基金项目
本文得到国家自然科学基金(数学基地科研训练及能力提高)项目资助和上海市科学技术委员会的资助,资助课题编号为13dz2260400。
文章引用
赵天骁,晁福刚,任韩. 运筹学中的指派问题
On the Assigning Problem in Operation Research[J]. 应用数学进展, 2016, 05(01): 45-50. http://dx.doi.org/10.12677/AAM.2016.51007
参考文献 (References)
- 1. Athanasiou, E. (2013) A Solomonic Solution to the Problem of Assigning a Private Indivisible Good. Games and Economic Behavior, 82, 369-387. http://dx.doi.org/10.1016/j.geb.2013.07.007
- 2. Bastianoni, S., Pulselli, F.M. and Tiezzi, E. (2004) The Problem of Assigning Responsibility for Greenhouse Gas Emissions. Ecological Economics, 49, 253-257. http://dx.doi.org/10.1016/j.ecolecon.2004.01.018
- 3. 田丰, 马仲蕃. 图与网络流理论[M]. 北京: 科学出版社, 1987.
- 4. 钱颂迪. 运筹学[M]. 北京: 清华大学出版社, 1997.