Advances in Applied Mathematics
Vol.06 No.04(2017), Article ID:21282,6
pages
10.12677/AAM.2017.64055
The Method of Fundamental Solutions for Laplace Equation on Irregular Domain by Using MATLAB
Kang Shan, Huantian Xie*, Wenxiang Wang, Yongkang Duan, Hongyue Lao
School of Mathematics and Statistics, Linyi University, Linyi Shandong
Received: Jun. 14th, 2017; accepted: Jul. 3rd, 2017; published: Jul. 6th, 2017
ABSTRACT
In this paper, Laplace equation on irregular domain is solved by MATLAB programming, which is the method of fundamental solutions. The result of numerical experiment shows the feasibility and accuracy of the meshless method.
Keywords:Irregular Domain, Laplace Equation, The Method of Fundamental Solutions, Meshless Method
不规则区域上Laplace方程基本解方法的MATLAB实现
单康，谢焕田*，王文祥，段永康，劳红月
临沂大学数学与统计学院，山东 临沂
收稿日期：2017年6月14日；录用日期：2017年7月3日；发布日期：2017年7月6日
摘 要
本文借助基本解方法通过MATLAB编程实现了二维不规则区域上Laplace方程的无网格数值求解，数值实验的结果表明了该方法的可行性和精确性。
关键词 :不规则区域，Laplace方程，基本解方法，无网格方法
Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
1. 引言
众所周知，Laplace方程 [1] (又称调和方程)
是最典型的椭圆型偏微分方程之一，它具有广泛的应用背景，例如静电学中的电势及牛顿万有引力理论中的引力势均满足该方程。传统上人们认为有限元法擅长计算复杂区域上椭圆型偏微分方程的适定问题 [2] ，但有限元法计算步骤较为复杂和抽象。与网格方法相比，无网格方法的最大优点是它不依赖于求解区域的网格划分，从而有效避免了网格划分所需要的巨大而繁重的工作量，特别是当数值求解过程中求解区域和边界条件随时间而变动时，无网格方法则具有传统网格方法无法比拟的优势 [3] [4] [5] [6] [7] 。鉴于以上分析，本文考虑二维不规则区域上Laplace方程的无网格方法。
首先利用Laplace算子的基本解作为基函数构造近似解，进而通过配置法利用边界条件得到数值解，数值实验的结果表明了此方法的可行性和精确性。
2. 基本解方法
基本解方法是一种数值求解椭圆型方程边值问题的边界型方法，它用微分算子的基本解的线性组合来逼近问题的解。由于基本解满足偏微分方程，只须考虑边界条件，因此属于边界型方法 [8] 。
考虑边值问题
其中
是微分算子，
是边界条件算子，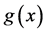
是已知函数，
是求解区域
的边界。
假设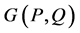
是微分算子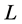
的基本解，则基本解方法的步骤可以简述如下：
1) 选取中心点
，其中
是包含求解区域
的封闭曲面(线)；
2) 构造
用于近似原问题的解
；
3) 选择边界点
，并令
特别地，当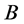
为线性算子时，有
4) 求解上述方程组得到数值解。
3. Laplace方程的基本解无网格方法
当微分算子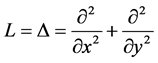
时，考虑二维Laplace方程的Dirichlet边值问题
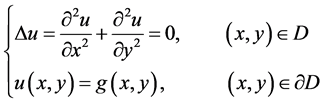
由文献 [9] 知微分算子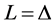
的基本解是
其中
。
此时，为求数值解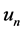
，只须求解线性方程组
其中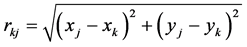
。
附录中给出了具体的MATLAB求解程序。
4. 数值实验
考虑二维不规则区域上Laplace方程的边值问题
其中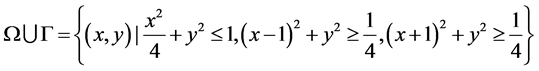
。求解区域的边界
是由一个大椭圆和两个小圆组成。该问题的真解是
。
为衡量数值解的精度，定义最大绝对误差如下
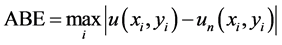
实验过程中，中心点的选择采用如下两种方案
方案I：在外边界(大椭圆)外部选择中心点如图1所示；
方案II：在内边界(两个小圆)的内部和外边界(大椭圆)外部分别选择中心点如图2所示。
为了考察中心点个数对数值解精度的影响，表1和表2分别列出了两种方案下不同中心点个数对应的最大绝对误差，从表中数据可以看出随着中心点个数的增加，数值解精度在不断提高，并且方案I的精度明显优于方案II。
Figure 1. Chosen points, numerical solution and absolute error for scheme I
图1. 标方案I的选点、数值解及误差情况
Figure 2. Chosen points, numerical solution and absolute error for scheme II
图2. 标方案II的选点、数值解及误差情况
Table 1. Comparison of ABE for scheme I
表1. 方案I的最大绝对误差比较
Table 2. Comparison of ABE for scheme II
表2. 方案II的最大绝对误差比较
5. 结论
通过本文结果可以知道，对于不规则区域上椭圆型偏微分方程的边值问题，采用基本解方法求解是方便可行的，同时启示我们构造高精度的无网格方法是值得研究的。
基金项目
大学生创新创业训练计划项目(201610452005)，山东省自然科学基金项目 (BS2015DX012)。
文章引用
单康,谢焕田,王文祥,段永康,劳红月. 不规则区域上Laplace方程基本解方法的MATLAB实现
The Method of Fundamental Solutions for Laplace Equation on Irregular Domain by Using MATLAB[J]. 应用数学进展, 2017, 06(04): 468-473. http://dx.doi.org/10.12677/AAM.2017.64055
参考文献 (References)
- 1. 姜礼尚. 数学物理方程讲义[M]. 第3版. 北京: 高等教育出版社, 2007.
- 2. 李荣华. 偏微分方程数值解法[M]. 北京: 高等教育出版社, 2005.
- 3. 程玉民. 无网格方法[M]. 北京: 科学出版社, 2015.
- 4. 刘欣. 无网格方法[M]. 北京: 科学出版社, 2011.
- 5. 张雄, 刘岩. 无网格法[M]. 北京: 清华大学出版社, 2004.
- 6. 吴宗敏. 散乱数据拟合的模型、方法和理论[M]. 北京: 科学出版社, 2007.
- 7. 徐传胜. 圣彼得堡数学学派研究[M]. 北京: 科学出版社, 2016.
- 8. 王钧, 孙方裕, 金邦梯. 基本解方法求解一个三维线弹性力学反问题[J]. 浙江大学学报(理学版), 2006, 33(2): 134-138.
- 9. Golberg, M.A. (1995) The Method of Fundamental Solutions for Poisson’s Equation. Engineering Analysis with Boundary Elements, 16, 205-213. https://doi.org/10.1016/0955-7997(95)00062-3
附录
for s=1:M
for t=1:M
q(s,t)=sqrt((node1(s,1)-node(t,1))^2+(node1(s,2)-node(t,2))^2);
A(s,t)=log(1/q(s,t));
end
end
alfa=A\f;
for t=1:M
qq=((X-node(t,1)).^2+(Y-node(t,2)).^2).^(1/2);
u=u+alfa(t).*log(1./qq);
end
期刊投稿者将享受如下服务：
1.投稿前咨询服务 (QQ、微信、邮箱皆可)
2.为您匹配最合适的期刊
3.24小时以内解答您的所有疑问
4.友好的在线投稿界面
5.专业的同行评审
6.知网检索
7.全网络覆盖式推广您的研究
投稿请点击：http://www.hanspub.org/Submission.aspx
期刊邮箱：aam@hanspub.org
NOTES
*通讯作者。