ABSTRACT

The paper deals with the numerical solutions of initial value problem of KdV equation on unbounded interval that approximates the solution of the Kortewego-de Vries equation, in which Hermite-Gauss nodes are used to collocate nodes of spectral collocation method. Selecting appropriately the relaxation factor $\sigma$ involved in the generalized Hermite functions approximation enables us to fit the asymptotic behaviors of exact solutions at infinity closely. Numerical results demonstrate its efficiency and high accuracy of this approach. Especially, it is much easier to deal with nonlinear equation.

Keywords:Kortewego-de Vries Equation, Initial Value Problem, Spectral Collocation Method of Hermite Functions, Hermite-Gauss Nodes

Kortewego-de Vries方程的Hermite函数谱配置方法

李冰冰，王天军

河南科技大学数学与统计学院，河南 洛阳

收稿日期：2019年3月31日；录用日期：2019年4月15日；发布日期：2019年4月22日

摘 要

以Hermite-Gauss节点为配置点，用带松弛因子的Hermite函数谱配置方法求数值解，逼近无界区域上的Kortewego-de Vries方程Cauchy问题的理论解，给出算法格式和相应的数值结果，表明所提算法格式的有效性和高精度。适当地选择松弛因子，使得数值解更好地匹配理论解的渐进行为，所给算法尤其适合于非线性问题。

关键词 :Kortewego-de Vries方程，初值问题，Hermite函数谱配置方法，Hermite-Gauss节点

Copyright © 2019 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

记 $R=\left\{x|-\infty <x<\infty \right\}$ ， $t>0,u\left(x,t\right)$ 是实值函数。为方便，记 $\frac{\partial }{\partial x}$ 为 ${\partial }_x$ 。考虑Kortewego-de Vries方程初值问题 [1] [2] [3]

$\{\begin{array}{ccc}{\partial }_{t}u+\gamma u{\partial }_{x}u+\nu {\partial }_x^{3}u-\mu {\partial }_x^{5}u=0,& x\in R,& t>0,\\ u\left(x,t\right)\to 0,& \left|x\right|\to \infty ,& t>0,\\ u\left(x,0\right)=\phi \left(x\right)& x\in R,& \end{array}$ (1)

其中 $\gamma ,\nu$ 和 $\mu$ 是常数。文献 [4] [5] 研究常微分方程的谱配置方法，文献 [6] 给出问题(1)的有界区域上混合问题的广义Jacobi逼近，文献 [7] 考虑了无界区域上三阶KdV方程( $\gamma =6,\nu =1,\mu =0$ )的Chebyshev-Hermite多项式时空谱配置方法，文献 [8] 提出了半无界区域上Fisher方程的Laguerre拟谱方法，文献 [9] 研究统计物理中无界区域上非线性Fokker-Planck方程的Hermite函数谱配点方法。考虑到问题(1)解的行波性态，为更好地吻合理论解在无穷远处的渐进行为，用含有因子 ${\text{e}}^{-{\left(\sigma x\right)}^2/2}$ 的插值函数逼近问题的理论解，利用高阶微分矩阵和一阶微分矩阵之间的关系处理高阶微分项，可以方便地构造非常简单的算法格式。

2. Lagrange插值函数及其微分矩阵

Hermite函数 ${\hat{H}}_n\left(y\right)$ 定义为

${\hat{H}}_n\left(y\right)=\frac{1}{\sqrt{2^{n}n!}}{e}^{-y^2/2}{H}_n\left(y\right),n\ge 0,y\in R.$

其中 $H_n\left(y\right)$ 表示 $n$ 阶Hermiter多项式。令 $y_j\left(0\le j\le N\right)$ 是 $H_{N+1}\left(y\right)=0$ 的根。以 $y_j$ 为节点的Hermite函数谱配置方法的Lagrange插值基函数为 [6] [10]

${\varphi }_j\left(y\right)=\frac{e^{-y^2/2}}{e^{-y_j^2/2}}\frac{H_{N+1}\left(y\right)}{\left(y-y_j\right)H_{{}_{N+1}}^{\text{'}}\left(y_j\right)},j=0,1,\cdots ,N,$

对任意 $u\left(y\right)\in C\left(R\right)$ ，其Lagrange插值函数为 $p_N\left(y\right)={\displaystyle \underset{j=0}{\overset{N}{\sum }}u\left(y_j\right){\varphi }_j\left(y\right),y\in R}$ 。对 $p_N\left(y\right)$ 求 $m$ 阶导数得，

$p_N^{\left(m\right)}\left(y\right)={\displaystyle \underset{j=0}{\overset{N}{\sum }}u\left(y_j\right)}{\varphi }_j^{\left(m\right)}\left(y\right).$

令

$D^{\left(m\right)}={\left({\varphi }_j^{\left(m\right)}\left(y_k\right)\right)}_{0\le k,j\le N},D:=D^{\left(1\right)},$

则由文献 [6] 中(3.68)和(7.93)

${\varphi }_j^{\left(1\right)}\left(y_k\right)=\{\begin{array}{cc}\frac{{\hat{H}}_N\left(y_k\right)}{\left(y_k-y_j\right){\hat{H}}_N\left(y_j\right)},& k\ne j,\\ 0,& k=j.\end{array}$ (2)

$D^{\left(m\right)}=D^m$ (3)

对那些解随 $\left|x\right|\to \infty$ 快速(或慢速)衰减的问题，用上述基函数不一定能得到高精度的数值误差结果。为了改进逼近精度，需要引入带伸缩因子的插值逼近，为此，给出下面的Hermite函数：

$H_n^{\sigma }\left(x\right)={\hat{H}}_n\left(\sigma x\right).$

相应的Lagrange插值基函数为：

${\varphi }_j^{\sigma }\left(x\right)=\frac{{\text{e}}^{-{\left(\sigma x\right)}^2/2}}{{\text{e}}^{-{\left(\sigma x_j\right)}^2/2}}\frac{H_{N+1}\left(\sigma x\right)}{\left(x-x_j\right)H_{{}_{N+1}}^{\text{'}}\left(\sigma x_j\right)},j=0,1,\cdots ,N.$

带松弛因子的微分矩阵记为

$D_{\sigma }^{\left(m\right)}={\left({\left({\varphi }_j^{\sigma }\left(y_k\right)\right)}^{\left(m\right)}\right)}_{0\le k,j\le N},D_{\sigma }:=D_{\sigma }^{\left(1\right)},$

和(2)式类似有：

${\left({\varphi }_j^{\sigma }\left(x_k\right)\right)}^{\left(1\right)}=\{\begin{array}{cc}\frac{H_N^{\sigma }\left(x_k\right)}{\left(x_k-x_j\right)H_N^{\sigma }\left(x_j\right)},& k\ne j,\\ 0,& k=j.\end{array}$

由 ${\varphi }_j^{\sigma }\left(x\right)={\varphi }_j\left(y\right)|{}_{y=\sigma x}$ 和(3)式知 $m$ 阶微分矩阵：

$D_{\sigma }^{\left(m\right)}=D_{\sigma }^m={\sigma }^m{D}^m$

3. Kortewego-de Vries方程的Hermite函数谱配置方法

3.1. 三阶Kortewego-de Vries方程配置方法

式(1)中令 $\gamma =\nu =1$ 和 $\mu =0$ 可得三阶Kortewego-de Vries方程 [1] ，考虑初值问题：

$\{\begin{array}{ccc}{\partial }_{t}u+u{\partial }_{x}u+{\partial }_x^{3}u=0,& x\in R,& t>0,\\ u\left(x,t\right)\to 0,& \left|x\right|\to \infty ,& t>0,\\ u\left(x,0\right)=\phi \left(x\right)& x\in R,& \end{array}$ (4)

用 $p_N^{\sigma }\left(x,t\right)={\displaystyle \underset{j=0}{\overset{N}{\sum }}u\left(x_j,t\right){\varphi }_j^{\sigma }\left(x\right),x\in R}$ ，逼近式(4)的解 $u\left(x,t\right)$ ，将其代入式(4)，得

$\{\begin{array}{cc}{\partial }_t{p}_N^{\sigma }\left(x_k,t\right)+p_N^{\sigma }\left(x_k,t\right){\partial }_x{p}_N^{\sigma }\left(x_k,t\right)+{\partial }_x^3{p}_N^{\sigma }\left(x_k,t\right)=0,& k=0,1,\cdots ,N,t>0,\\ p_N^{\sigma }\left(x_k,0\right)=\phi \left(x_k\right),& k=0,1,\cdots ,N.\end{array}$ (5)

式(5)等价于

$\{\begin{array}{l}{u}^{\prime }\left(x_0,t\right)=-{\displaystyle \underset{j=0}{\overset{N}{\sum }}u\left(x_j,t\right){\left({\varphi }_j^{\sigma }\left(x_0\right)\right)}^{\left(3\right)}}-u\left(x_0,t\right){\displaystyle \underset{j=0}{\overset{N}{\sum }}u\left(x_j,t\right){\left({\varphi }_j^{\sigma }\left(x_0\right)\right)}^{(1)}},\\ \begin{array}{cccc}& & & \begin{array}{cccc}\begin{array}{ccc}\begin{array}{cccc}\cdots & & \cdots & \end{array}& \cdots & \end{array}& & & \end{array}\end{array}\\ u^{\prime }\left(x_N,t\right)=-{\displaystyle \underset{j=0}{\overset{N}{\sum }}u\left(x_j,t\right){\left({\varphi }_j^{\sigma }\left(x_N\right)\right)}^{\left(3\right)}}-u\left(x_N,t\right){\displaystyle \underset{j=0}{\overset{N}{\sum }}u\left(x_j,t\right){\left({\varphi }_j^{\sigma }\left(x_N\right)\right)}^{(1)},}\\ u\left(x_j,0\right)=\phi \left(x_j\right)\begin{array}{cc},& j=0,1,\cdots N.\end{array}\end{array}$ (6)

令 $X\left(t\right)={\left(u\left(x_0,t\right),u\left(x_1,t\right),\cdots ,u\left(x_N,t\right)\right)}^T,X_0={\left(\phi \left(x_0\right),\phi \left(x_1\right),\cdots ,\phi \left(x_N\right)\right)}^T$ ，式(6)的矩阵形式为

$\{\begin{array}{cc}\frac{\text{d}X\left(t\right)}{\text{d}t}=-{\sigma }^3{D}^{3}X\left(t\right)-\sigma A\left(t\right)DX\left(t\right)& t>0\\ X\left(0\right)=X_0.& \end{array}$ (7)

这里矩阵 $A\left(t\right)=\left(a_{ij}\left(t\right)\right)$ ，为 $\left(N+1\right)\times \left(N+1\right)$ 矩阵，其元素为

显然， $A\left(t\right)DX\left(t\right)$ 是非线性项。

3.2. 数值结果

用格式(7)求解式(4)。在时间方向用步长为 $\tau$ 的Crank-Nicolson格式离散式(7)，得

$\{\begin{array}{c}\left(I+\frac{1}{2}\tau {\sigma }^{3}D\right)X\left(t+\tau \right)=\left(I-\frac{1}{2}\tau {\sigma }^3{D}^3\right)X\left(t\right)-\frac{1}{2}\tau \sigma \left(A\left(t+\tau \right)DX\left(t+\tau \right)+A\left(t\right)DX\left(t\right)\right),\\ t=0,\tau ,2\tau ,\cdots T-\tau ,\\ X\left(0\right)=X_0.\end{array}$ (8)

由于式(7)式是关于 $X\left(t\right)$ 的非线性方程(或关于其分量的非线性方程组)，实际计算时应用解非线性方程(组)的Newton迭代方法，需要计算迭代矩阵。为方便起见，用如下的迭代方法：在时间方向 $t+\tau$ 这一层进行迭代：

$\{\begin{array}{c}\left(I+\frac{1}{2}\tau {\sigma }^{3}D\right)X_{n+1}\left(t+\tau \right)=\left(I-\frac{1}{2}\tau {\sigma }^3{D}^3\right)X\left(t\right)-\frac{1}{2}\tau \sigma \left(A\left(t+\tau \right)D{X}_n\left(t+\tau \right)+A\left(t\right)DX\left(t\right)\right),\\ t=0,\tau ,2\tau ,\cdots T-\tau ,\\ X\left(0\right)=X_0.\end{array}$ (9)

设定迭代终止条件：对给定的 $\epsilon >0$ ，如果 $\left|X_{n+1}\left(t+\tau \right)-X_n\left(t+\tau \right)\right|\le \epsilon$ ，即得 $t+\tau$ 的值 $X\left(t+\tau \right)$ 。

三阶Kortewego-de Vries方程有精确孤波解 [1] [6] ：

$u=12\kappa {\text{sech}}^2\left(\kappa \left(x-4{\kappa }^{2}t-x_0\right)\right),$ (10)

其中 $\kappa$ 和 $x_0$ 是给定的参数。

用 $L^{\infty }$ -范数

$E_N=\underset{0\le j\le N}{\max }\left|u\left(x_j,t\right)-P_N^{\sigma }\left(x_j,t\right)\right|$

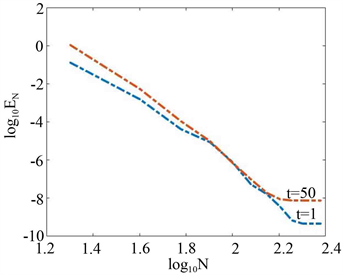
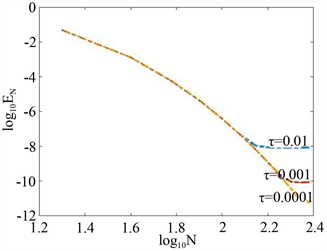
度量数值误差。图1给出 $t=1$ 和不同 $\tau$ ，数值解和理论解的误差 $E_N$ 的常用对数 ${\log }_{10}{E}_N$ 随 ${\log }_{10}N$ 的关系。可以看出，数值误差随 $N$ 的增加及 $\tau$ 的减小而快速衰减，空间方向达到谱精度；图2给出 $t=1$ 和 $t=50$ 误差，可以看出对较大的 $t$ 所提算法格式仍然有效。

图1. $\kappa =0.3,\sigma =0.3$

图2. $\kappa =0.3,\sigma =0.3,\tau =0.001$

3.3. 五阶Kortewego-de Vries方程配置方法

用 $p_N^{\sigma }\left(x,t\right)={\displaystyle \underset{m=0}{\overset{N}{\sum }}u\left(x_j,t\right){\varphi }_j^{\sigma }\left(x\right),x\in R}$ ，逼近式(1)的解，将其代入式(1)，得

$\{\begin{array}{cc}{\partial }_t{p}_N^{\sigma }\left(x_k,t\right)+\gamma p_N^{\sigma }\left(x_k,t\right){\partial }_x{p}_N^{\sigma }\left(x_k,t\right)+\nu {\partial }_x^3{p}_N^{\sigma }\left(x_k,t\right)-\mu {\partial }_x^5{p}_N^{\sigma }\left(x_k,t\right)=0,& k=0,1,\cdots ,N,t>0,\\ p_N^{\sigma }\left(x_k,0\right)=\phi \left(x_k\right)& k=0,1,\cdots ,N.\end{array}$ (11)

和式(7)相似，式(11)的矩阵形式为

$\{\begin{array}{cc}\frac{\text{d}X\left(t\right)}{\text{d}t}=\left(\mu {\sigma }^5{D}^5-\nu {\sigma }^3{D}^3\right)X\left(t\right)-\gamma \sigma A\left(t\right)DX\left(t\right),& t>0\\ X\left(0\right)=X_0.& \end{array}$ (12)

4. 数值结果

用格式(12)求解式(1)。在时间方向用步长为 $\tau$ 的Crank-Nicolson格式离散式(12)，得

$\{\begin{array}{c}\left(I-\frac{1}{2}\tau \left(\mu {\sigma }^5{D}^5-\nu {\sigma }^3{D}^3\right)\right)X\left(t+\tau \right)=\left(I+\frac{1}{2}\tau \left(\mu {\sigma }^5{D}^5-\nu {\sigma }^3{D}^3\right)\right)X\left(t\right)\\ -\frac{1}{2}\tau \gamma \sigma \left(A\left(t+\tau \right)DX\left(t+\tau \right)+A\left(t\right)DX\left(t\right)\right),\\ t=0,\tau ,2\tau ,\cdots T-\tau ,\\ X\left(0\right)=X_0.\end{array}$ (13)

由于式(13)式是关于 $X\left(t\right)$ 的非线性方程(或关于其分量的非线性方程组)，用类似式(9)的迭代方法：在时间方向 $t+\tau$ 这一层进行迭代：

$\{\begin{array}{c}\left(I-\frac{1}{2}\tau \left(\mu {\sigma }^5{D}^5-\nu {\sigma }^3{D}^3\right)\right)X_{n+1}\left(t+\tau \right)=\left(I+\frac{1}{2}\tau \left(\mu {\sigma }^5{D}^5-\nu {\sigma }^3{D}^3\right)\right)X\left(t\right)\\ -\frac{1}{2}\tau \gamma \sigma \left(A\left(t+\tau \right)D{X}_n\left(t+\tau \right)+A\left(t\right)DX\left(t\right)\right)\\ t=0,\tau ,2\tau ,\cdots T-\tau ,\\ X\left(0\right)=X_0.\end{array}$ (14)

设定迭代终止条件：对给定的 $\epsilon >0$ ，如果 $\left|X_{n+1}\left(t+\tau \right)-X_n\left(t+\tau \right)\right|\le \epsilon$ ，即得 $t+\tau$ 的值 $X\left(t+\tau \right)$ 。

式(1)有精确解 [11]

$u\left(x,t\right)={\eta }_0+A{\text{sech}}^4\left(\kappa \left(x-ct-x_0\right)\right),$

其中 $x_0$ 和 ${\eta }_0$ 是任意常数，

$A=\frac{105{\nu }^2}{169\mu \gamma },\kappa =\sqrt{\frac{\nu }{52\mu }},c=\gamma {\eta }_0+\frac{36{\nu }^2}{169\mu }.$

用 $u\left(x,t\right)$ 作为测试函数，用 $E_N$ 度量数值误差。图3给出 $t=1$ 和不同的 $\tau$ 及 ${\log }_{10}{E}_N$ 随 ${\log }_{10}N$ 的变化关系。可以看出，数值误差随 $N$ 的增加及数值误差 $\tau$ 的减小而快速衰减，空间方向达到谱精度；图4给出 $t=1$ 和不同的伸缩因子 $\sigma$ 数值误差 ${\log }_{10}{E}_N$ 随 ${\log }_{10}N$ 的变化关系，可以发现对适当小的 $\sigma$ 数值误差更小。但如何选取最佳伸缩因子是一个未解决的问题。

图3. $\sigma =0.365,\mu =\gamma =1,\nu =1.1,{\eta }_0=0$

图4. $\tau =0.001,\mu =\gamma =1,\nu =1.1,{\eta }_0=0$

5. 结论

以带松弛因子的Hermite函数配置方法求问题(1) (三阶和五阶)的数值解，逼近无界区域上的KdV方程的理论解。由于基函数含有因子 ${\text{e}}^{-{\left(\sigma x\right)}^2/2}$ ，通过适当选取松弛因子 $\sigma$ 可以使数值解能更好地吻合理论解在无穷远处的渐进行为，所给算法尤其适合于非线性问题。

基金项目

国家自然科学基金项目(11371123)；S201810464034。

文章引用

李冰冰,王天军. Kortewego-de Vries方程的Hermite函数谱配置方法
Generalized Hermite Function Spectral-Collocation Method for KdV Equations[J]. 应用数学进展, 2019, 08(04): 631-637. https://doi.org/10.12677/AAM.2019.84070

参考文献