Advances in Applied Mathematics
Vol.
09
No.
01
(
2020
), Article ID:
33933
,
10
pages
10.12677/AAM.2020.91007
A Set of New Criteria for the Iterative Discrimination of Subdivision of Nonsingular H-Matrices
Wenwen Jiang, Qing Tuo*
College of Mathematics and Statistics, Jishou University, Jishou Hunan
Received: Dec. 19th, 2019; accepted: Jan. 7th, 2020; published: Jan. 14th, 2020

ABSTRACT
In this paper, we produced a set of new conditions for subdivided and iterative criteria of nonsingular H-matrices by the method of subdivided region and selected iterative coefficient, based on the nonsingular H-matrix and α-diagonally dominant matrix the relationship between diagonally dominant matrices. These conditions improved some recent results. Finally, several numerical examples were given to illustrate their validity.
Keywords:Non-Singular H-Matrix, α-Diagonally Dominant Matrix, Irreducible, Nonzero Elements Chain

一组关于非奇异H-矩阵的细分迭代判别新条件
蒋雯雯,庹 清*
吉首大学数学与统计学院,湖南 吉首

收稿日期:2019年12月19日;录用日期:2020年1月7日;发布日期:2020年1月14日

摘 要
本文根据非奇异H-矩阵与α-对角占优矩阵之间的关系,通过细分矩阵的下标区间,以及构造出新的迭代系数,得出了一组关于非奇异H-矩阵的细分迭代判别新条件,该条件改进了近期的某些结果,最后给出的几个数值算例说明了其有效性。
关键词 :非奇异H-矩阵,α-对角占优矩阵,不可约,非零元素链

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
非奇异H-矩阵是一种很重要的矩阵类。它在数学物理、统计学、神经网络等各个领域中都有着重要的地位。对于判定线性方程组(尤其是超大型方程组)是否具有稳定解时,往往需要先通过判定其系数矩阵是否为非奇异H-矩阵来体现。如:当一个线性方程组的系数矩阵为非奇异H-矩阵,那么该方程组对Jacobi,Gauss-seidel,SOR,SSOR,AOR等经典算法均是收敛的,即该方程组具有稳定解。因此,非奇异H-矩阵判定问题一直是研究的热点,近年来国内外许多学者给出了一些实用的判定条件。
范迎松、徐仲、陆全等人在文献 [1] 中先使用了细分矩阵的下标区间的办法,并由新构造的递进系数提出了关于非奇异H-矩阵新的判别准则;尹军茹等人在文献 [2] 中使用细分矩阵下标区间的方法,构造出新的迭代系数得到了不一样的判别准则。在此基础上,山瑞平等人在文献 [3] 中,根据广义严格对角占优矩阵与非奇异H-矩阵之间蕴含的关系,细分了下标区间,并构造出不同的正对角矩阵,从而得到更好的判定条件。此外,庹清、刘长太等学者近年来在此领域也得出了一些很好的结果(见文献 [4] [5] [6] [7])。
本文中,用
来表示n阶复(实)矩阵的集合。设
, 记
。为使所讨论的矩阵为非零矩阵且所论内容有意义,以下假设:在全文中,
,且规定
。
定义1:设
,若
,则称A为对角占优矩阵,记为
;若
,则称A为严格对角占优矩阵,记为
;若存在正对角阵X,使得X右乘到矩阵A后的乘积矩阵为严格对角占优矩阵,则称A为广义严格对角占优矩阵,记为
。
定义2:设
,,若
,则称A为α-对角占优矩阵,记为
;若
,则称A为严格α-对角占优矩阵,记为
;若存在正对角阵X,使得X右乘到矩阵A后的乘积矩阵为严格α-对角占优矩阵,则称A为广义严格α-对角占优矩阵,记为
。
定义3:设 为不可约矩阵,
为不可约矩阵,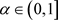 ,若
,则称A为不可约α-对角占优矩阵。
,若
,则称A为不可约α-对角占优矩阵。
定义4:设
为α-对角占优阵,
,若对满足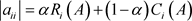 的每个下标i,存在非零元素链
,使得
,则称A为具非零元素链α-对角占优矩阵。
的每个下标i,存在非零元素链
,使得
,则称A为具非零元素链α-对角占优矩阵。
引理1 [8] 设
,, 当且仅当
。
引理2 [8] 设
为不可约α-对角占优矩阵,且至少有一个对角占优行,则
。
引理3 [9] 设
为具有非零元素链α-对角占优矩阵,则
。
以下是下标集的符号解释:
,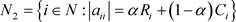 ,
,
,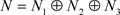 。
。
若
,则
;若
,显然
。为使所论内容有意义,以下假设:
,。
文献 [3] 给出的主要结果如下:
首先,划分下标区间:令
,,。
记,
时,
;
时,
;
时,
,
,
,
 ,
,
,
。
定理. 设
, ,若存在
,使满足
,若存在
,使满足
,
,
则A是非奇异H-矩阵。
2. 主要结果
设
,,将不占优行的下标区间划分为m个区间,即
,其中m是任意正整数。
具体分法即,
,
,
根据划分规则易知:
或为空集。
为叙述方便,引入以下符号:
,, ;
;
,,;
,,,
,,
,
,
 ,
,
,
由上易知,
,,。
2.1. 定理1
设
,,若存在
,使满足:
(1)
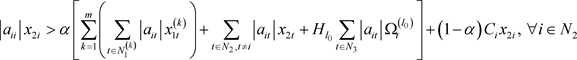 (2)
(2)
则A是非奇异H-矩阵。
证明
由于
,得到
,从而
。
由于
,m是任意正整数,所以
。
根据定义得到,
又因为
,故
,。
根据(1)式和(2)式,存在
,可取充分小的正数
,使
同时满足:
(3)
(4)
再根据
, 的定义,以及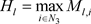 ,
,对于任意
,有:
,
,对于任意
,有:
,
又因为
 ,所以得到:
,所以得到:
,
即
,
当
时,易知上述等式依旧成立。
因为
,所以
,
综上,取
且充分小,得:
(5)
下面构造正对角矩阵
,记
,其中:
 ,
,
1)
,由(3)式得,
2)
,由(4)式得,
3)
,因为
,,所以
,再由(5)式得,
综上所述,
,,总是能够成立,即满足
,所以
,根据引理4,则
,证毕。
注1 本文定理1对文献 [3] 的定理1有所改进,由于
,故做每步迭代时都有所进步(即判定条件比文献 [3] 的弱)。
我们可以在定理1中取
,得出推论1,如下所示。
2.1.1. 推论1
设
,若存在
,使满足
则A是非奇异H-矩阵。
注2 由于
,故做每步迭代时都有所进步(即判定条件比文献 [1] 的定理1条件弱),也就是说本文推论1推广了文献 [1] 的定理1。
还可以在定理1中取
,得出推论2。
2.1.2. 推论2
设
,若存在
,使满足
则A是非奇异H-矩阵。
同理可以推出下面两个定理:
2.2. 定理2
设
,,矩阵A不可约,若存在
,使满足
(6)
(7)
且(6)或(7)中至少有一个严格不等式成立,则A是非奇异H-矩阵。
2.3. 定理3
记,
,
,
设
,,若存在
,使满足
(8)
(9)
且(8)或(9)中至少有一个严格不等式成立,若对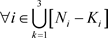 ,存在非零元素链
,使得
,则A是非奇异H-矩阵。
,存在非零元素链
,使得
,则A是非奇异H-矩阵。
3. 数值实例
例设
。
易知
,当取
时,容易算得
(保留四位小数,后同),
。
继而能够得出:
(文献 [1] 结果);
(本文结果),
当
 时,根据
时,根据
显然A不满足文献 [1] 中定理1的条件,不能判定其为非奇异H-矩阵。
但是,由本文得出的结果,有
显然矩阵A满足本文定理1的条件,可知矩阵A是非奇异H-矩阵。
其中取正对角矩阵:
,
所以
,B是一个严格α-对角占优矩阵。
致谢
感谢陈茜等同学对本文提供的建议和帮助。
基金项目
国家自然科学基金(11461027)和湖南省教育厅科研基金(16A173),吉首大学研究生创新基金(JGY201932)。
文章引用
蒋雯雯,庹 清. 一组关于非奇异H-矩阵的细分迭代判别新条件
A Set of New Criteria for the Iterative Discrimination of Subdivision of Nonsingular H-Matrices[J]. 应用数学进展, 2020, 09(01): 50-59. https://doi.org/10.12677/AAM.2020.91007
参考文献
- 1. 范迎松, 陆全, 徐仲, 高慧敏. 非奇异H-矩阵的一组判定条件[J]. 高校应用数学学报A辑, 2011, 26(4): 474-480.
- 2. 尹军茹, 徐仲, 陆全. 非奇H-矩阵的细分迭代判别准则[J]. 工程数学学报, 2013, 30(3): 433-441.
- 3. 山瑞平, 陆全, 徐仲, 张骁. 非奇H-矩阵的一组细分迭代判定条件[J]. 应用数学学报, 2014, 37(6): 1130-1139.
- 4. 庹清, 陈茜. 关于“一类非奇异H-矩阵判定的新条件”一文的注记[J]. 计算数学, 2019, 41(2): 219-224.
- 5. 刘长太. 非奇异H矩阵迭代式充分条件[J]. 计算数学, 2017, 39(3): 328-336.
- 6. Gan, T.-B. and Huang, T.-Z. (2003) Simple Criteria for Nonsingular H-Matrices. Linear Algebra and Its Applications, 374, 317-326.
https://doi.org/10.1016/S0024-3795(03)00646-3
- 7. Berman, A. and Plemmons, R.J. (1979) Nonnegative Matrix in the Mathematical Sciences. Academic Press, New York.
https://doi.org/10.1016/B978-0-12-092250-5.50009-6
- 8. 谢清明. 判定广义对角占优矩阵的几个充分条件[J]. 工程数学学报, 2006(4): 757-760.
- 9. 孙玉祥. 广义对角占优矩阵的充分条件[J]. 高等学校计算数学学报, 1997(3): 216-223.
NOTES
*通讯作者。







 为不可约矩阵,
为不可约矩阵,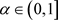 ,若
,则称A为不可约α-对角占优矩阵。
,若
,则称A为不可约α-对角占优矩阵。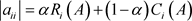 的每个下标i,存在非零元素链
,使得
,则称A为具非零元素链α-对角占优矩阵。
的每个下标i,存在非零元素链
,使得
,则称A为具非零元素链α-对角占优矩阵。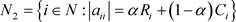 ,
,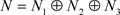 。
。 ,
, ,若存在
,使满足
,若存在
,使满足 ;
; ,
,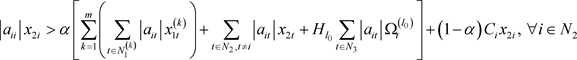 (2)
(2)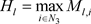 ,
,对于任意
,有:
,
,对于任意
,有: ,所以得到:
,所以得到: ,
,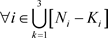 ,存在非零元素链
,使得
,则A是非奇异H-矩阵。
,存在非零元素链
,使得
,则A是非奇异H-矩阵。 时,根据
时,根据