Advances in Applied Mathematics
Vol.
09
No.
03
(
2020
), Article ID:
34537
,
12
pages
10.12677/AAM.2020.93038
The Maximal Wiener Index of Unicyclic Graph with Given Diameter and Order
Huimin Wang, Yuanpei Wang, Chenchen Cao, Qiang Sun*
School of Mathematical Science, Yangzhou University, Yangzhou Jiangsu

Received: Feb. 25th, 2020; accepted: Mar. 9th, 2020; published: Mar. 16th, 2020

ABSTRACT
The Wiener index of a graph is one of the most very well-researched topological indices, i.e. graph theoretic invariants of molecular graphs. Some interesting questions remain largely unsolved despite being easy to state and comprehend. In this paper, we investigate a conjecture proposed by DelaVina and Waller [1], namely, the graphs of order 2d + 1 and diameter d have Wiener index less or equal than the cycle of order 2d + 1. In this paper, we proved that this conjecture is true for unicyclic graphs with vertices outside of the cycle not too many.
Keywords:Wiener Index, Unicyclic Graph, Maximum

给定直径和阶的具有最大Wiener指标的单圈图
王惠敏,王元培,曹陈琛,孙强*
扬州大学数学科学学院,江苏 扬州
收稿日期:2020年2月25日;录用日期:2020年3月9日;发布日期:2020年3月16日

摘 要
图的Wiener指标是图论中研究的比较深刻的拓扑指标之一,结果很丰富,同时也有许多有趣的问题没有被解决,尽管这些问题很容易表述也很容易被理解。在这篇文章中,我们着重研究由DelaVina和Waller [1] 提出的一个猜想,即:点数是2d + 1,直径为d的图的Wiener指标都不超过点数是2d + 1的圈的。本文证明了该猜想对于单圈且圈外顶点数不多的图是正确的。
关键词 :Wiener指标,单圈图,最大值

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 研究背景
1.1. 研究历史
令
是一个简单的连通图。图G的Wiener指标是指图G中所有点对的距离和,即
其中
表示
之间的距离。
Wiener指标是由Harold Wiener [2] 最先发现的,用以研究烷烃沸点的一种分子拓扑指标,它是指无环烷烃图中碳原子对之间键的数量的集合。1971年,Hosoya证明了Wiener指标等于分子图中的直径矩阵的元素总和的一半,由此,Wiener指标的定义被延伸到了有圈图中。
在近些年中,Wiener指标的最大与最小问题吸引了许多学者的研究,并有了一定的发现。Entringer,Jackson和Snyder [3] 在1976年用到了
的定义。随着有关于Wiener指标的深入,更多的结果被发现 [4] [5]。在所有阶为n的图中,路具有最大Wiener指标,星图具有最小Wiener指标。有关于给定条件下图的Wiener指标极值问题有许多,如:周波教授 [6] 研究了给定点数与匹配数的图的最小Wiener指标。于桂海教授 [7] 刻画了给定周长的具有极大与极小Wiener指标的图。在这些问题中,由DelaVina和Waller [1] 提出的猜想极大地促进了Wiener指标的研究:
猜想1:阶为
,直径为
的连通图G中,具有最大Wiener指标的图是圈。
为了研究这个猜想,我们将问题范围从连通图缩小到单圈图。在本文中,我们将研究给定直径和阶的具有最大Wiener指标的单圈图。我们将证明以下定理:
定理1:在阶为
,直径为d,圈的阶为
的单圈图G中,如果
,则
,圈
。
1.2. 术语介绍
我们简单介绍一下本文会用到的符号,对未说明的符号请参考文献 [5]。在本文中,我们主要研究简单的无向图
, 分别表示图的点集和边集。
表示点
之间的距离,即连接
两点的最短路的长度。连接点u的边数称为u的度,度为1的点称为悬挂点。路是由无重复的顶点和边构成的序列
,对于
,边
的顶点为
和
。如果路的顶点
,则它构成圈。连通的无圈图称为树,只有一个圈的图称为单圈图。
我们定义
是阶为
的单圈图,它有着阶为
的圈
与链接在圈上的树
。当
的阶为0时,
不存在。
为了方便证明中的叙述,下面我们介绍几个特殊的定义:
1.2.1. 定义1
令
是阶为
,直径为
的扫帚树,其图形是阶为
的星状树,其中一条边被分割成
条边的路。如图1所示,我们将路上的顶点标为
,并且顶点
是度为
的点。令其他与顶点
相连的悬挂点按逆时针标为
。
图1. 定义1-
1.2.2. 定义2
令图H是图G的子图。
是图H的边,
是图
的边,则图
定义为由图 删去边
并加上边
的图。
1.2.3. 定义3
在图
中,令
和
是图G的子图,图
和
分别由图
和
变化而来,则有
, 和
。
1.2.4. 定义4
令
,定义
是
均为扫帚树
,且
与圈C之间以边
相连的图G,其中d为图的直径,
为图的阶,i为图中所有阶不为0的扫帚树的总数。
1.2.5. 定义5
在图
中,若扫帚树
和
满足
,则令
。
2. 引理和结论
为了证明定理1,我们首先引入几个引理。
2.1. 引理1
扫帚树
的Wiener指标为:
2.2. 引理2
令图G为一个阶为
,直径为d的单圈图,圈C是图G的一个阶为
的子图。如图2,令
为图
的一个度大于等于3的顶点,同时与
和
相连,且有
和
到圈C的直径是
到圈C的直径加1,即
。保证图G的直径不变,将图G变化为图
。当
时,有
。
图2. 引理1
证明:图
都是图G删去边
和
得到的部分,其中
并且
。保证图G的直径不变,令
,则有
。
当
时,有
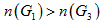 ,则
,即
。
,则
,即
。
2.3. 引理3
令图G为一个阶为
,直径为d的单圈图,圈C是图G的一个阶为
的子图。如图3,
是图
的子图,且扫帚树
是图G的子图且链接于同一个顶点v。
, 且
,。令
,当
时,有
。
图3. 引理3
证明:由条件可知:
。
明显当
时,
,即
。
2.4. 引理4
令图G为一个阶为
,直径为d的单圈图,圈C是图G的一个阶为
的子图。如图4,
是图
的子图,且扫帚树
是图G的子图且链接于同一个顶点v。
, 或1,且
。令
,当
时,有
。
图4. 引理4
证明:令
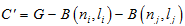
其中
。
当
, 时,
,则有
。所以,当
时,
。
当
, 时,
时,则有
。所以,当
时,
。
2.5. 结论1 (扫帚变换)
令图G为一个阶为
,直径为d的单圈图,圈C是图G的一个阶为
的子图。通过以下步骤可以将单圈图G中链接在圈C上的任意一支树
变成扫帚树,使得Wiener指标增加。令
与圈C链接于圈上的点
。
第一步:当
时,反复进行引理2中的变换,直到
的所有悬挂点都与顶点
的距离相等,在此过程中G的Wiener指标不断增大。
第二步:由引理3可知,当
时,任意选取两个扫帚树
满足条件:
和
,通过反复进行将
和
变为
和
的变化,我们可以不断增加Wiener指标,直到
或者
。再根据引理4,当
时,将
和
变为
,此过程中G的Wiener指标不断增大,反复步骤二直至
变成扫帚树。
2.6. 引理5 [8]
阶为m的圈C上的一个顶点u到圈上其他各点的距离和为:
阶为m的圈C的Wiener指标为:
2.7. 引理6
令图G是一个阶为
,直径为d的单圈图,圈C是图G的一个阶为
的子图。在单圈图G上有扫帚树
链接在圈C上的点
上。令
,当
时,有
。
证明:令
,有
。
当
时,有
,即
。
2.8. 引理7
在图
中,令集合
,图中必定存在一支中心扫帚树
有
。若不存在,必定可以通过引理6获得一个存在中心扫帚树且Wiener指标更大的图
。
证明:当
时,令唯一的一支扫帚树为中心扫帚树。
当
时,若集合
中不存在
,反复通过引理6中的变化,我们必定可以得到一个有更大Wiener指标,且集合
不为空的情况。
当集合
中只有一个
,则令
上两支扫帚树中直径较大的一支为中心扫帚树。
当集合
中有两个或以上
,如果不存在
,我们将情况分为以下三种:
情况1:在图
中,将扫帚树任意标为
,, 和
,若存在
和
,且
,,我们可以得出:
,,。因此,我们可以得到:
且
;或者
。此时令
与
中直径较大的一支为中心扫帚树。
情况2:在图
中,将扫帚树顺时针标为
,,, 和
。显然该图可以被刻画为:
,。假设
。令
且
,很明显Wiener指标会增长,有如下
。因此总存在一个有着更大Wiener指标的图
存在不为空的P。
情况3:在图
,,将扫帚树顺时针标为
,,, 等,假设存在
和
,我们可以得到
且
,,条件相互矛盾,因此不可能存在不包含中心扫帚树的P,该情况不存在。
2.9. 引理8
在图
中,
,,则存在一个图
,其中
,当
,有
。
证明:任意选取一支扫帚树记为
。如图5,
链接于圈C上顶点
,从
开始将圈上的顶点顺时针(或逆时针)记为
。
和
是在
上的两个顶点,令
时,该图的Wiener指标会增加。
当k是奇数时,
为奇数,设
。
图5. 引理8
和
之间Wiener指标的变化为:
和
之间Wiener指标的变化为:
自身Wiener指标的变化为:
和圈之间Wiener指标的变化为:
和圈之间Wiener指标的变化为:
由此,图的Wiener指标变化为:
当
,,有
。
当
时,该图的Wiener指标会不断增加。
当k是偶数时,
为偶数,设
。
就如同奇数情况下,图的Wiener指标变化为:
当
,,有
。
当
时,该图的Wiener指标会不断增加。
根据引理7,存在一支中心扫帚树
,我们将它标为
,从它开始将图上扫帚树顺时针依次标为
,可以找到一支顶点数不为0的
满足:
,,我们将图上扫帚树和圈上的点重新标记,将
记为
(特别地,当
时,将中心扫帚树记为
),
链接在圈C上的顶点为
,从
开始将圈上的顶点顺时针(或逆时针)记为
,将中心扫帚树记为
,保证
。
当
中
时,根据
中
的大小,分类讨论:
情况1:当
,且
中
或
时,对
反复上述变化。
情况2:当
,且
中
时,有:
如果
,对中心扫帚树
作一次上述变化,此时可以得到图
,且
。
再根据引理6,令
删去边
,加上边
,可以得到
,且
。根据不等式的传递性,
,此时
,回到情况1。
如果
,根据引理6,令
删去边
,加上边
,此时
,回到情况1。
情况3:当
且
中
时,对
作一次上述变化,可以得到图
,且
。
再根据引理6,令
删去边
,加上边
,可以得到
,且
。根据不等式的传递性,
,反复进行该变化。
情况4:当
中
时,见引理9,引理8得证。
当
中
时,对中心扫帚树
作一次上述变化,此时可以得到图
,且
,此时回到
的情况。
2.10. 引理9
如图6,在引理8中,当
且
, 上的悬挂点标记为
,令
,该图Wiener指标增大。
证明:根据引理7,存在一支中心扫帚树
,我们将它标为
,从它开始将图上扫帚树顺时针依次标为
,可以找到一支顶点数不为0的
满足:
,,我们将图上扫帚树和圈上的点重新标记,将
记为
(特别地,当
时,将中心扫帚树记为
),
链接在圈C上的顶点为
,从
开始将圈上的点顺时针(或逆时针)记为
,将中心扫帚树记为
,保证
。
图6. 引理9
情况1:当k是奇数时,
为奇数,设
。
很明显,
和
之间Wiener指标变化为:
和
之间Wiener指标的变化为:
和圈之间Wiener指标变化为:
和圈之间Wiener指标变化为:
由此,该图的Wiener指标变化有:
当
,,有
。
情况2:当k是偶数时,
为偶数,设
。
与奇数情况类似,该图的Wiener指标变化有:
当
时,
,有
。
3. 定理1的证明
为了证明定理1,我们需要刻画阶为
,直径为d的单圈图的图形。令圈上的顶点数为
。根据结论1,我们可以证明当
时,在任意阶为
,直径为d的单圈图中,具有最大的Wiener指标的图可以被刻画为
,其中
。
此时根据引理7,我们可以确定一个中心扫帚树的存在。根据引理8,我们可以知道当
时,对于任意的图
必定存在着一个具有更大Wiener指标的图
,依次推理,当
时,图G变为圈
。
因此,在阶为
,直径为d的单圈图中,具有最大Wiener指标的图可以被刻画为圈
,即定理1得证。
致谢
本论文历经6个月时间完成,在研究与写作途中有许多的障碍与困难,但是都在老师与同学们的帮助下度过。在此我们诚挚感谢我们的论文指导老师,因为老师的悉心指导与不断督促,我们才能在课题研究与论文写作上不断精益求精。同时也感谢本文所涉及到的各位专家学者,本文很多的思路与启发都是来自于各个学者的研究文献。最后感谢我的同学们,本文是我们共同完成,一同创作的结果。本文因我们学术水平有限,该论文仍有不足之处,恳请各位学者与学友批评指正。
基金项目
扬州大学大学生科创基金项目,本项目得到“江苏高校品牌专业建设工程资助项目(数学与应用数学,PPZY2015B109)”经费资助,同时也得到国家自然科学基金项目(基金号:11801494)的资助。
文章引用
王惠敏,王元培,曹陈琛,孙 强. 给定直径和阶的具有最大Wiener指标的单圈图
The Maximal Wiener Index of UnicyclicGraph with Given Diameter and Order[J]. 应用数学进展, 2020, 09(03): 318-329. https://doi.org/10.12677/AAM.2020.93038
参考文献
- 1. DeLaVina, E. and Waller, B. (2008) Spanning Trees with Many Leaves and Average Distances. Electronic Journal of Combinatorics, 15, 16. https://doi.org/10.37236/757
- 2. Wiener, H. (1947) Structural Determination of Paraffin Boiling Points. Journal of the American Chemical Society, 69, 17-20. https://doi.org/10.1021/ja01193a005
- 3. Entringer, R.C., Jackson, D.E. and Snyder, D.A. (1976) Distance in Graphs. Czechoslovak Mathematical Journal, 26, 283-296.
- 4. Bondy, J.A. and Murty, U. (2008) Graph Theory. Graduate Texts in Mathematics. 5th Edition, Springer, New York. https://doi.org/10.1007/978-1-84628-970-5
- 5. Broersma, H. and Tuinstra, H. (1998) Independent Trees and Hamilton Cycles. Journal of Graph Theory, 29, 227-237. https://doi.org/10.1002/(SICI)1097-0118(199812)29:4<227::AID-JGT2>3.0.CO;2-W
- 6. Du, Z. and Zhou, B. (2010) Minimum on Wiener Indices of Trees and Unicyclic Graphs of the Given Matching Number. MATCH Commu-nications in Mathematical and in Computer Chemistry, 63, 101-112.
- 7. Yu, G. and Feng, L. (2010) On the Wiener Index of Unicyclic Graphs with Given Girth. Ars Combinatoria, 94, 361-369.
- 8. 汤自凯. 具有次大Wiener指数的单圈图[J]. 湖南文理学院学报(自然科学版), 2006, 18(4): 2-5.
NOTES
*通讯作者。









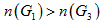 ,则
,即
。
,则
,即
。