Advances in Applied Mathematics
Vol.
10
No.
01
(
2021
), Article ID:
39820
,
4
pages
10.12677/AAM.2021.101007
“零点定理”在生活中的应用
符繁强,陈云烁
遵义职业技术学院,贵州 遵义

收稿日期:2020年12月14日;录用日期:2021年1月3日;发布日期:2021年1月19日

摘要
在数学发展的历史长廊中,闭区间上连续函数的性质,为数学学科的发展奠定了理论基础。本文主要介绍闭区间上连续函数的零点存在性定理,并例举出零点定理在求解椅子放稳、电梯升降、以及政府对宏观经济的调控等实际生活中的应用,最后归纳总结出应用零点定理求解实际问题的一般步骤。
关键词
闭区间,连续函数,零点定理,实践与应用
The Application of “Zero Theorem” in Life
Fanqiang Fu, Yunshuo Chen
Zunyi Vocational and Technical College, Zunyi Guizhou

Received: Dec. 14th, 2020; accepted: Jan. 3rd, 2021; published: Jan. 19th, 2021

ABSTRACT
In the historical corridor of mathematics development, the nature of continuous functions on closed intervals has laid a theoretical foundation for the development of mathematics. This article mainly introduces the zero-point existence theorem of continuous functions on closed intervals, and exemplifies the application of the zero-point theorem in solving the problem of chair stabilization, elevator lifting, and government regulation of the macro-economy, and finally summarizes the application of the zero-point theorem general steps for solving practical problems.
Keywords:Closed Interval, Continuous Function, Zero Theorem, Practice and Application

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
闭区间上连续函数的零点定理是《高等数学》课程教学中必不可少的内容,根据零点定理可以引出《高等数学》中几个重要的定理例如:介值定理、拉格朗日中值定理等。数学来源于生活,必将应用到生活中,零点定理不论是在数学中或者物理中都具有广泛的应用 [1]。例如:椅子放稳、电梯升降、以及政府对宏观经济的调控等实际生活问题,本文将在零点定理的基础上,建立数学模型,针对以上所提出的问题进行求解,并归纳总结出求解的一般步骤 [2]。
2. 零点定理的介绍
零点定理 [3] [4]:设函数 在闭区间 上连续,且 与 异号,即 ,那么在开区间 内至少存在一点 ,使得 。
(即:方程 在 内至少存在上一个实根)

几何意义:对于曲线 ,如果曲线的两个端点处于水平线x轴两侧,则曲线与x轴至少有一个交点.
3. 零点定理的应用
零点定理的应用背景非常广泛,下面将介绍定理在不同背景下的应用。
例1 [5] [6]:将四条腿长度相同的椅子放置在凹凸不平的地面上,现分析椅子是否能平稳的放置在地面。
分析:图1中A、B、C、D为椅子的四只脚,坐标系原点选椅子中心,坐标轴选为其对角线,椅子的移动位置可以由正方形沿坐标原点旋转的角度 唯一表示。现假设某椅子脚与地面的垂直距离为y,显然y是关于 的函数,记为 ,由于正方形的中心对称性,可以用对应的两个脚与地面的距离之和来表示两个脚与地面的距离关系,记 为A、C的距离之和; 为B、D的距离之和,显然 、 ,并且是 的连续函数,要使椅子能在地面放稳至少有三只脚同时着地,即对于任意的 , 至少有一个为0,不妨设当 时, (即A、C其中一点着地) (即B、D着地)。
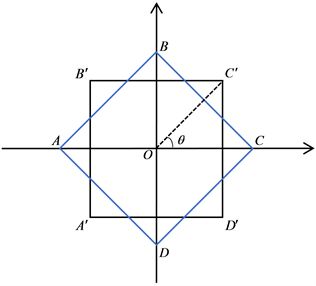
Figure 1. The four corners of the chair
图1. 椅子四角图
上述命题可描述为如下命题。
命题:设函数 是关于 的非负连续函数,对任意的 ,有 ,且 ,则有存在 ,使 。
证明:现将椅子旋转90˚,则椅子对角线AC与BD互换,由 变为 。
令
则有 和 ,由 的连续性及连续函数的中值定理,必存在一个 ,使
,即则有存在 ,使 。
例2:某小区住户甲早上8点从42层坐电梯楼下,8点3分到一楼,住户乙8点从一楼返回42层,8点3分到达,试证明住户甲与住户乙在某个时刻会经过相同位置高度。
证明:根据题意,现以时间t为横坐标,电梯所在高度h为纵坐标,建立直角坐标系,如图2所示,直线AB为住户甲所在电梯的运动轨迹,直线DC为住户甲所在电梯的运动轨迹。现假设住户甲与住户乙在某个时间t内处于同一高度,记为: 。

Figure 2. The trajectory of the elevator
图2. 电梯运动轨迹
记直线AB: ;
记直线CD: 。
令 。
因为 连续,因此 在 上式连续的。
从而 (H为电梯所在的高度)
根据零点定理可知,则在区间 上至少存在一个点 ,使得 ,从而 。
例3:在经济快速增长的时代,政府对市场经济实行必要的调控,是维持经济良性发展的有效手段,假设市场经济增长函数为 ,政府调控经济增长函数为 ,试证明在某一时刻市场增长价格与政府调控价格相同。
证明:
因为 连续,因此 为连续函数。
从而
表示 时刻市场经济增长函数 的值大于政府调控经济增长函数 的值
表示 时刻市场经济增长函数 的值小于政府调控经济增长函数 的值,其中a为常数,表示政府调控价格与市场价格的差值。
根据零点定理可知,则在区间 上至少存在一个点 ,使得 ,从而 ,即至少存在一个确定时刻 ,使得政府调控价格与市场价格相同,从而达到经济宏观调控的目的。
4. 零点定理求解一般步骤
通过实例的分析,得到零点定理求解不同背景的一般步骤:
第一步 作辅助函数:将定理中 用 替换,写出相对应的方程;
第二步 找函数异号值:在自变量的取值范围内找出两个异号的自变量值;
第二步 寻找“0”点位置:通过异号性找出“0”点位置。
文章引用
符繁强,陈云烁. “零点定理”在生活中的应用
The Application of “Zero Theorem” in Life[J]. 应用数学进展, 2021, 10(01): 62-65. https://doi.org/10.12677/AAM.2021.101007
参考文献
- 1. 余荣. 零点定理的应用[J]. 武汉工程大学学报, 2010(11): 108-110.
- 2. 孟广武. 连续函数零点定理的应用[J]. 聊城大学学报(自然科学版), 2013, 26(4): 1-5.
- 3. 陈海霞. 数学在生活中应用的典型案例[J]. 数学学习与研究: 教研版, 2008(7): 125.
- 4. 杨桂芹. 浅谈数学在生活中的应用[J]. 中国校外教育, 2007(5): 107.
- 5. 孙秀娟, 王新霞, 王春. 高等数学案例教学法[J]. 高师理科学刊, 2012, 32(3): 88-90.
- 6. 王芳芳, 王永静. 应用数学实例分析[J]. 新课程(下), 2016(1): 130-131.