Advances in Applied Mathematics
Vol.
12
No.
09
(
2023
), Article ID:
71885
,
8
pages
10.12677/AAM.2023.129377
具交叉扩散和弱Allee效应的反应扩散方程图灵斑图研究
郑加乐,郑锦楠,陈凯璇
广州大学数学与信息科学学院,广东 广州
收稿日期:2023年8月4日;录用日期:2023年9月1日;发布日期:2023年9月6日

摘要
本文提出了一类具有交叉扩散的反应扩散方程,用于研究一类具有弱Allee效应的捕食食饵反应扩散模型在交叉扩散驱动下的图灵斑图动力学现象。研究发现,交叉扩散是该模型产生图灵斑图必不可少的条件,如果没有交叉扩散,则模型不会发生图灵失稳。同时,通过选择不同参数,我们发现模型的斑图现象十分丰富,可以出现点斑图、点–线混合斑图、线斑图三种类型。
关键词
图灵斑图,交叉扩散,捕食食饵

Turing Pattern Study of Reaction Diffusion Equations with Cross Diffusion and Weak Allee Effect
Jiale Zheng, Jinnan Zheng, Kaixuan Chen
School of Mathematics and Information Science, Guangzhou University, Guangzhou Guangdong
Received: Aug. 4th, 2023; accepted: Sep. 1st, 2023; published: Sep. 6th, 2023

ABSTRACT
This article proposes a class of reaction diffusion equations with cross diffusion to study the Turing pattern dynamics of a predator-prey reaction diffusion model with weak Allee effect driven by cross diffusion. Research has found that cross diffusion is an essential condition for the model to generate Turing patterns. Without cross diffusion, the model will not experience Turing instability. At the same time, by selecting different parameters, we found that the pattern phenomenon of the model is very rich, which can appear in three types: spots pattern, spots-stripes mixed pattern and stripes pattern.
Keywords:Turing Pattern, Cross-Diffusion, Predator-Prey

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在自然界中,许多生物总是混杂在一起,它们之间的关系非常复杂,包括捕食、寄生、共存和竞争等,并将形成一个庞大而复杂的食物网。其中,捕食关系最为常见。如果一种生物以另一种为食,我们称前者为“掠食者”,后者为“猎物”。比如,蛇–鹰,斑马–狮子,虫–鸟等就是典型的捕食者与猎物关系。1926年,Lotka [1] 和Volterra [2] 提出了著名的Lotka-Volterra捕食–被捕食模型,该模型是微分方程理论在生物科学中应用的重要成果。尽管该模型本身比较简单,不适用于现实生活中的许多问题,但它促进了生物数学的发展。如今,许多学者 [3] [4] [5] [6] [7] 研究捕食和被捕食模型的相关问题,这些模型最初是从Lotka-Volterra模型慢慢演化而来的。正如数学家和生物学家所探索的,他们提出了两种功能性反应:猎物依赖和捕食者依赖,这可以用来更准确地描述捕食者和猎物之间的关系。在食饵依赖型中,Holling-II功能型反应 已被广泛研究。其中,张 [8] 研究了如下具有的第二类功能反应函数的捕食食饵模型:
(1)
其中, 分别代表食饵和捕食者的密度, 都是正参数,分别代表食饵的内禀增长率、环境最大容纳量、捕食者的攻击速率、消耗率、转化率、死亡率。张 [8] 研究该模型并将它分为四个参数区域:强Allee区、弱Allee区、无Allee区和灭绝区。其中,弱Allee区的参数条件满足:
(2)
然而,上面描述的ODE模型只反映了种群随时间的演化,但在现实世界中,有一个绝对不能忽视的因素——空间。例如,近年来,新型冠状病毒肆虐。由于病毒很容易通过空气传播,如果数学家和生物学家在研究病毒时只考虑时间因素,没有考虑病毒在空间传播造成的空间异位,那么研究所得到的结果就不太真实。同样,在动物世界中,总是存在着空间位置的变化,为了生存、为了捕食、为了逃避捕食、为了躲避自然灾害,等等,他们必须有空间上的扩散。因此,在研究问题时,最好考虑空间因素,在捕食–被捕食ODE模型中引入所谓的“扩散项”,使研究结果更加准确。这样所建立的方程称为反应扩散方程,近年来受到国内外学者的广泛关注。例如,Subrata Dey等 [9] 研究了一个具有广义捕食者和自由扩散的捕食者–食饵系统:Arancibia-Ibarra,Claudioet等 [10] 研究了一个扩散Holling-Tanner捕食者–食饵模型,为捕食者提供了一个替代的食物来源:Hu等 [11] 研究了一个强耦合的扩散捕食者–食饵系统:Tang和Song [12] 研究了一个具有群集行为和交叉扩散的捕食者–食饵模型:
(3)
这里, 。 表示自由扩散系数,它表示物种因自身原因的扩散速率, 代表交叉扩散系数,它代表物种因另一物种而交叉形成的扩散速率。因此,受到张 [8] 和Tang [12] 的启发,我们提出了如下的模型:
(4)
这里,我们将区域Ω限制至二维空间 : 是拉普拉斯算子: 指Neuman边界条件,代表着物种不会跑出这个边界: , 则代表着物种正的初值,符合现实意义。
本文中,我们将在第二部分简述ODE模型(1)的一些结论,并分析PDE模型(4)在弱Allee条件(2)下发生图灵失稳的条件,第三部分则是在这个图灵失稳条件下进行数值模拟,展现丰富的图灵斑图现象,第四部分对模型提出总结与展望。
2. 理论分析
2.1. ODE模型稳定性分析
为了方便讨论问题,我们定义如下的非线性函数
(5)
这里,
(6)
容易知道,当 时,我们有 , ,因而,我们知道 是一个经典的二次函数,在第一象限是先单调递增再单调递减, ,并且有且仅有一个正根p满足 ,因此, 在第一象限也仅有一个正根p。
由(5),我们可以将方程(1)简写成:
(7)
为了研究(7)的平衡点稳定性,我们必须深入研究非线性函数 的性态。对 求导得:
(8)
令 ,则有 ,因而, 有且仅有唯一的正根,记为
(9)
综上所述,我们知道函数 在 之间大于0,在 之间小于0,并且 在 之间单调递增,在 之间单调递减。诸如,当我们取 , , , ,则 , ,那么 的函数图像如图1所示。
由张 [8] 对于(7)的弱Allee部分的平衡点的分析,我们知道,模型(7)永远有两个边界平衡点: , 。而(7)的正平衡点 , , 只有在当 时才会存在。下面的定理揭示了正平衡点 的稳定性。
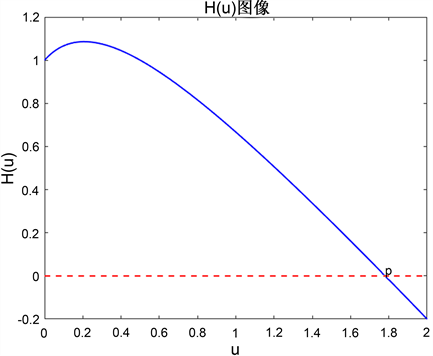
Figure 1. Example of image
图1. 图像示例
定理1.
1) 在 时是不稳定的,在 时是稳定的。
2) 当 时,模型(7)发生Hopf分岔。
证明:
1) 容易知道,模型(7)在 的雅可比矩阵为:
(10)
那么,J的特征方程为:
(11)
其中,T,D分别是J的迹和行列式,表达式为:
(12)
由上面对于 的分析,我们知道当 , , ;当 , , 可以立即得到结论。
2) 当 ,我们知道 ,并且横截条件为
(13)
由著名的Poincare-Andronov-Hopf分支定理,结论显然成立。
2.2. PDE模型稳定性分析
为了得到在 发生图灵失稳的参数条件,我们总是假定 在ODE模型(7)中总是存在并且稳定的,即下列条件总是成立的:
(14)
现在假设
(15)
是模型(4)在 的线性化系统的非常数解。这里, 且 也叫做波数, 是二维空间行向量, 是空间变量。则模型(4)的线性化系统的特征方程为:
(16)
这里,
(17)
(18)
这里:
(19)
容易知道,当 时, ,故而。因此,能够使得发生图灵失稳现象的只能是当对于适当的k,有 发生的情况。现记 并定义如下函数:
ℊ (20)
为了得到图灵失稳的条件,我们需要寻找恰当的 使得ℊ 在某些 上小于0,由于 (见(12)),通过对二元函数ℊ 结合图像分析,我们很容易知道当满足以下任一条件时,那么“ℊ 在某些 上小于0”:
(i) ;或(ii) , 且 (21)
综上所述,模型(4)发生图灵失稳的参数条件为:(14) & (21)。
现在假设交叉扩散 ,那么 , ,依据判别条件(21),我们知道,如果没有交叉扩散系数,则有 恒成立,换句话说,模型(4)将不会发生图灵失稳现象。因此,在该模型中,交叉扩散系数至关重要。
3. 数值模拟
现在,我们对模型(4)在条件(14) & (21)下进行数值模拟。通过如下的五点差分格式
(22)
可以实现对拉普拉斯算子做离散化,这里h指的是空间步长。再者,通过设置在正平衡点附近的随机小扰动作为初值。鉴于捕食者与食饵所形成的图灵斑图是一致的,因而我们仅展示食饵的斑图情况。以下三个例子中,我们用Matlab进行数值模拟,并将网格固定为50 × 50,空间步长为1,时间步长为0.01,演变时间为50,000。
例1:如果我们选择参数 , , , , , ,并且 满足条件(14)。至于扩散系数,我们选取 。此时,若选取 ,则 满足条件(21)的(i),此时,可以得到如下图2线斑图。我们可以看到,食饵在此时以线的形式分布着,并且是交叉纵横的。在线上,食饵的密度高。但在线外,食饵的密度低。
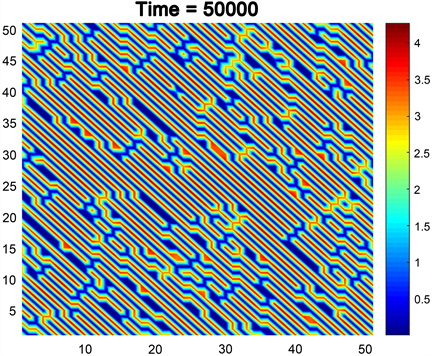
Figure 2. Stripes pattern
图2. 线斑图
例2.如果我们选择参数 , , , , , ,并且 满足条件(14)。至于扩散系数,我们选取 , , , ,此时, , , ,符合条件(21)的(ii)。此时,图灵斑图如图3所示。可以看到,当时间较大时,不同于例1的是,食饵不再以线形分布,而是聚集成了一个个的斑点,并且越靠近斑心中心,种群密度就越高,越远离斑心中心则密度越低。这种斑图称为“点斑图”。
例3.如果我们选择参数 , , , , , ,并且 满足条件(14)。至于扩散系数,我们选取 , , , ,此时, , , ,符合条件(21)的(ii)。此时,图灵斑图如图4所示。可以看到,当时间较大时,不同于例1,2的是,食饵不仅仅是单纯以圆点状或线型分布,而是圆点与线互相竞争,最终点、线共同存在。这叫作“点–线”混合斑图。
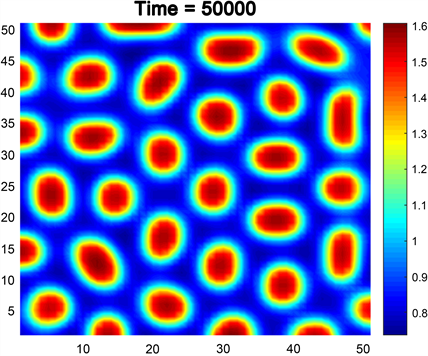
Figure 3. Spots pattern
图3. 点斑图
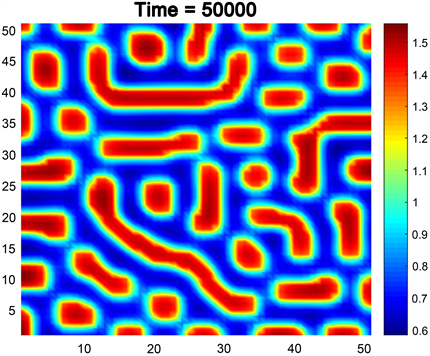
Figure 4. Mixed pattern
图4. 混合斑图
4. 总结展望
本文通过对一个具有交叉扩散和弱Allee效应的反应扩散方程捕食食饵模型进行研究,我们发现交叉扩散系数是产生图灵失稳必不可少的条件。同时。通过选取不同参数,可以生成丰富多彩的图灵斑图(Turing pattern),包括点斑图、线斑图和点–线混合斑图,这反映了在不同的参数条件下种群在空间上的分布情况,对种群生态学的认识、研究与防控是具有一定的意义的。
值得展望的是,本文只讨论了弱Allee效应情况下的斑图情况,但对于强Allee效应、无Allee效应的情况又有什么情况发生?有什么异同点?这是值得后续进行研究的。此外,如果参数选择得当,还可以出现螺旋波斑图等更加美丽的斑图现象,这同样也值得关注。
文章引用
郑加乐,郑锦楠,陈凯璇. 具交叉扩散和弱Allee效应的反应扩散方程图灵斑图研究
Turing Pattern Study of Reaction Diffusion Equations with Cross Diffusion and Weak Allee Effect[J]. 应用数学进展, 2023, 12(09): 3834-3841. https://doi.org/10.12677/AAM.2023.129377
参考文献
- 1. Lotka, A.J. (1925) Elements of Physical Biology. Williams and Wilkins, New Work.
- 2. Volterra, V. (1926) Variazionie fluttuazioni del numero dindividui in specie animali conviventi. Memorie Accad. d. L. Roma, 2, 31-113. https://zbmath.org/52.0450.06
- 3. Scaramangas, A. and Broom, M. (2022) Aposematic Signalling in Prey-Predator Systems: Determining Evolutionary Stability When Prey Populations Consist of a Single Species. Journal of Mathematical Biology, 85, Article No. 13. https://doi.org/10.1007/s00285-022-01762-y
- 4. Nadim, S.S., Samanta, S., Pal, N., et al. (2022) Impact of Preda-tor Signals on the Stability of a Predator-Prey System: A Z-Control Approach. Differential Equations and Dynamical Systems, 30, 451-467. https://doi.org/10.1007/s00285-022-01762-y
- 5. Shi, D.Y. and Zhang, S.H. (2022) Unconditional Superconver-gence of the Fully-Discrete Schemes for Nonlinearprey-Predator Model. Applied Numerical Mathematics, 172, 118-132. https://doi.org/10.1016/j.apnum.2021.10.002
- 6. Qi, H.K., Meng, X.Z., Hayat, T. and Hobiny, A. (2022) Station-ary Distribution of a Stochastic Predator-Prey Model with Hunting Cooperation. Applied Mathematics Letters, 124, 107662. https://doi.org/10.1016/j.aml.2021.107662
- 7. Lu, C. (2022) Dynamical Analysis and Numerical Simula-tions on a Crowley-Martin Predator-Prey Model in Stochastic Environment. Applied Mathematics and Computation, 413, 126641. https://doi.org/10.1016/j.amc.2021.126641
- 8. 张晓漩. 食饵受额外捕食影响的捕食-食饵模型的动力学[D]: [硕士学位论文]. 广州: 广州大学, 2022. https://doi.org/10.27040/d.cnki.ggzdu.2022.000458
- 9. Dey, S., Banerjee, M. and Ghorai, S. (2022) Analytical Detection of Stationary Turing Pattern in a Predator-Prey System with Generalist Predator. Mathematical Modelling of Natural Phenomena, 17, Article No. 33. https://doi.org/10.1051/mmnp/2022032
- 10. Arancibia-Ibarra, C., Bode, M., Flores, J., Pettet, G. and van Heijster, P. (2021) Turing Patterns in a Diffusive Holling-Tanner Predator-Prey Model with an Alternative Food Source for the Predator. Communications in Nonlinear Science and Numerical Simulation, 99, 105802. https://doi.org/10.1016/j.cnsns.2021.105802
- 11. Hu, G.P. and Feng, Z.S. (2020) Turing Instability and Pattern Formation in a Strongly Coupled Diffusive Predator-Prey System. International Journal of Bifurcation and Chaos, 30, 2030020. https://doi.org/10.1142/S0218127420300207
- 12. Tang, X.S. and Song, Y.L. (2015) Cross-Diffusion Induced Spatiotemporal Patterns in a Predator-Prey Model with Herd Behavior. Nonlinear Analysis: Real World Applica-tions, 24, 36-49. https://doi.org/10.1016/j.nonrwa.2014.12.006