International Journal of Mechanics Research
Vol.
08
No.
01
(
2019
), Article ID:
29272
,
11
pages
10.12677/IJM.2019.81007
Free Vibration Analysis of Rectangular Thin Plates Based on Spectral Method
Zhongkai Zhao1, Junhua Zhang1, Yanqi Liu2
1College of Mechanical Engineering, Beijing Information and Science Technology University, Beijing
2Beijing Municipal Institute of Labor Protection, Beijing

Received: Feb. 21st, 2019; accepted: Mar. 7th, 2019; published: Mar. 15th, 2019

ABSTRACT
A Chebyshev spectral method without both stiffness and mass matrices is proposed. Free vibrations of rectangular thin plates with clamped boundaries are researched by Chebyshev spectral method. Based on the partial differential equations of thin plates for free vibrations, the equations of eigen frequencies are educed by separating variables. Relationship between frequencies and physical parameters of materials is established. Referring to Chebyshev spectral method, high order derivative matrix is obtained which is a power operation of first order derivative matrix. The eigen frequency matrix equation of free vibration of thin plates is derived, but there is no stiffness matrix and no mass matrix. An example of clamped rectangular thin plate is solving by two methods. Compared with finite element method, efficiency and convergence of spectral method are verified. Comparing results by two methods, the frequencies and modes of the plate are basically consistent.
Keywords:Spectral Method, Free Vibration, Chebyshev Polynomials, Rectangular Thin Plates
基于谱方法的矩形薄板自由振动分析
赵中凯1,张君华1,刘彦琦2
1北京信息科技大学,机电工程学院,北京
2北京市劳动保护科学研究所,北京

收稿日期:2019年2月21日;录用日期:2019年3月7日;发布日期:2019年3月15日

摘 要
提出了一种无刚度矩阵及无质量矩阵的切比雪夫谱方法,基于该方法研究了四边固支矩形薄板的自由振动特性。根据薄板自由振动的偏微分方程,采用分离变量法推导了薄板自由振动的特征频率方程,建立了薄板各物理参数与自由振动频率之间的关系式。基于切比雪夫谱方法,构造出满足四边固支矩形薄板自由振动微分方程的高阶求导矩阵,得到了薄板自由振动的特征频率矩阵方程,该方程不含刚度矩阵和质量矩阵。通过算例和有限元方法比较,验证了切比雪夫谱方法的高效性与收敛性。对比两种方法的计算结果,算例中薄板的频率变化规律以及各阶振型变化规律基本一致。
关键词 :谱方法,自由振动,切比雪夫多项式,矩形薄板

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
弹性矩形薄板是工程中常见的结构形式,如国际空间站的太阳能电池帆板 [1] ,电子设备中的芯片,高速铁路中的轨道板 [2] 等,弹性矩形薄板的自由振动特性受到了各国学者的广泛关注,并且提出了相关的模型和计算方法。Ritz [3] 基于变分原理,假设薄板的形函数为三角函数与双曲函数的乘积,分析了自由边界条件下方形薄板的横向自由振动,得到了自由边界条件下方形薄板横向自由振动的特征值及节线图。Mindlin [4] 考虑了转动惯量和剪切变形,导出了各向同性弹性板的应力应变关系、运动微分方程以及能量函数。Gorman [5] 提出了求解四边固支矩形薄板自由振动解析解的叠加方法,该方法将振型函数表示为两个函数的乘积,并将振型函数分为双对称、双反对称、对称反对称三种形式,计算过程比较复杂。钟阳 [6] 从四边固支矩形薄板自由振动的基本方程出发,在哈密顿体系中使用辛几何方法得到了四边固支矩形薄板自由振动的精确解。Liew [7] 提出了pb-2瑞利里兹方法,该方法以边界函数和正交多项式构造出里兹试函数。Zhou和Cheung [8] 在pb-2瑞利里兹方法的基础上提出了切比雪夫里兹方法,分析了矩形板的三维振动,该方法以一组边界函数与切比雪夫多项式的乘积作为里兹试函数。陈林 [9] 等基于改进的傅里叶级数法研究了任意边界条件下矩形薄板的振动特性。薄板自由振动的控制方程为四阶椭圆型偏微分方程,上述方法一般都需要假设满足位移边界的位移试函数,根据变分原理得到薄板的特征频率方程。
近年来,一些新的理论和方法也得到了发展。Silling [10] 提出了一套非局部连续力学体系——近场动力学理论。同时,有关谱方法的研究也逐渐增多 [11] - [17] 。Orszag等根据不同的权函数对谱方法进行了分类,系统地总结了谱方法数值稳定性、收敛性的分析理论。Canuto等在前人研究基础上阐明了谱方法在流体力学应用中的关键内容,包括谱逼近的正交多项式、二维映射方法等。Shen等应用谱方法研究了高阶微分方程的边值问题。Shen等将谱方法与有限元方法结合,采用谱元方法对薄壁梁前4阶自由振动的频率和振型进行了分析。Trefethen提出了一种切比雪夫谱方法,该方法采用切比雪夫插值点构造了任意区间上任意连续函数的一阶求导矩阵。
从目前国内外的研究现状来看,采用切比雪夫谱方法研究板壳振动的文献不多。本文在Trefethen的研究基础上,利用一阶求导矩阵构造出满足四边固支矩形薄板自由振动微分方程的高阶求导矩阵,得到了四边固支矩形薄板自由振动的特征频率矩阵方程。与传统的Ritz法、Galerkin法等不同的是,由切比雪夫谱方法得到的特征频率矩阵方程不含有刚度矩阵和质量矩阵。通过算例和有限元方法比较,验证了切比雪夫谱方法的正确性。
2. 位移方程和边界条件
分析如图1所示弹性矩形薄板的横向自由振动问题,一般采用基尔霍夫假定,忽略剪切变形和转动惯量对薄板弯曲变形的影响,薄板横向自由振动的位移方程可以写成式(1) [18] :
Figure 1. Rectangular plate
图1. 矩形薄板
 (1)
(1)
(1)式中: 为薄板的抗弯刚度,E为薄板材料的弹性模量,
为薄板的抗弯刚度,E为薄板材料的弹性模量, 为薄板材料的泊松比,
为薄板材料的泊松比, 为薄板材料的密度,h为薄板的厚度。双调和算子的运算满足式(2):
为薄板材料的密度,h为薄板的厚度。双调和算子的运算满足式(2):
 (2)
(2)
假设薄板在时域做简谐运动,将时间变量与空间变量分离,则横向自由振动位移w可以写成式(3):
 (3)
(3)
将(3)式带入(1)式,得到特征频率方程式(4):
 (4)
(4)
(4)式中: 为波数,
为波数, 为薄板的自由振动频率。对于四边固支边界,薄板在边界上不发生横向位移,也不产生由位移变化引起的转角。因此,四边固支薄板的边界关系满足式(5)。根据文献 [14] 的研究,薄板的固支边界条件为微分方程的第一类边界条件和第二类边界条件的组合。
为薄板的自由振动频率。对于四边固支边界,薄板在边界上不发生横向位移,也不产生由位移变化引起的转角。因此,四边固支薄板的边界关系满足式(5)。根据文献 [14] 的研究,薄板的固支边界条件为微分方程的第一类边界条件和第二类边界条件的组合。
 (5)
(5)
3. 切比雪夫谱方法
切比雪夫多项式是以俄罗斯数学家Pafnuty Lvovich Chebyshev命名的一系列多项式序列。切比雪夫多项式是一类完备的正交多项式,在数值计算中切比雪夫多项式的收敛性和数值稳定性优于一般的多项式,如泰勒级数 [19] 。第一类切比雪夫多项式的表达式如式(6)所示:
 (6)
(6)
(6)式中:n为非负整数。第一类切比雪夫多项式存在交错点组,使得 ,在数值分析中被称为切比雪夫插值点,是在区间[−1,1]选取的N + 1个不同的点,切比雪夫插值点的定义如式(7)所示:
,在数值分析中被称为切比雪夫插值点,是在区间[−1,1]选取的N + 1个不同的点,切比雪夫插值点的定义如式(7)所示:
 (7)
(7)

Figure 2. Distribution of Chebyshev points (N = 8)
图2. N = 8时切比雪夫插值点的分布
当N = 8时,切比雪夫插值点的分布如图2所示。对于任意区间 ,切比雪夫插值点满足式(8)的映射关系;同理,对于任意矩形区域
,切比雪夫插值点满足式(8)的映射关系;同理,对于任意矩形区域 ,
,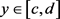 ,切比雪夫插值点满足式(9)的映射关系:
,切比雪夫插值点满足式(9)的映射关系:
 (8)
(8)
 (9)
(9)
根据文献 [18] 所提出的切比雪夫谱方法,区间[−1,1]上的1阶切比雪夫谱求导矩阵 满足式(10):
满足式(10):
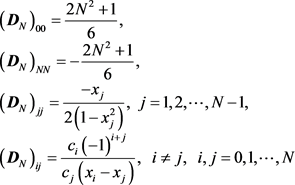 (10)
(10)
(10)式中:i、j分别代表1阶切比雪夫谱求导矩阵中第i + 1行、第j + 1列, 满足式(11):
满足式(11):
 (11)
(11)
采用切比雪夫谱方法求解高阶微分方程时,高阶切比雪夫谱求导矩阵可以表达为1阶切比雪夫谱求导矩阵的高次幂,如式(12)所示:
 (12)
(12)
将对应的各阶切比雪夫谱求导矩阵带入特征频率方程(4),可以得到如下的特征频率矩阵方程:
 (13)
(13)
(13)式中: 代表克罗内克积 [20] 。
代表克罗内克积 [20] 。
4. 数值算例与结果分析
4.1. 算例
算例为一四边固支方形薄板,如图3所示。边长为L = 2 m,弹性模量E = 2.10 × 109 Pa,薄板厚度h = 0.01 m,泊松比ν = 0.3,薄板的密度ρ = 7800 kg/m3。

Figure 3. Finite element model
图3. 有限元模型
4.2. 频率分析
有限元模型是在ANSYS 15.0中建立的,采用shell181单元,方形网格边长为0.01 m,网格数量40,000,节点数量40,401。在切比雪夫谱方法中,切比雪夫插值点数取25,求解算法在MATLAB R2017b中实现,矩阵规模25 × 25。四边固支方形薄板横向自由振动频率的计算结果如表1和图4所示。
分别采用切比雪夫谱方法和有限元方法计算了算例的前25阶频率。由表1可知,随着频率的增大,切比雪夫谱方法与有限元方法计算结果之间的误差越来越大,最大值出现在25阶频率,但是最大误差只有0.31%。同时在前25阶频率中,出现了6对重复的频率值,分别为2阶和3阶、7阶和8阶、9阶和10阶、14阶和15阶、18阶和19阶、23阶和24阶。与有限元方法所需的网格数量相比,切比雪夫谱方法选取的切比雪夫插值点个数很少,矩阵规模远远小于有限元方法,计算机内存占用更少,计算效率更高。
在上述研究的基础上,根据1~25阶频率的特点,选取了两组频率,分别得到了两组频率值随切比雪夫插值点数变化的规律。如图4所示,第一组为9阶和10阶,频率值相同;第二组为24和25阶,频率
Table 1. Frequencies and errors calculated by spectral method and FEM
表1. 谱方法和有限元方法计算的频率及误差
值不同。由图4可知,当插值点数大于12时,9阶和10阶频率值快速收敛,基本不再变化;当插值点数大于14时,24阶和25阶频率值快速收敛,基本不再变化。计算结果表明,采用切比雪夫谱方法研究算例的前25阶频率时,采用15~25个切比雪夫插值点可以保证计算结果的收敛性。
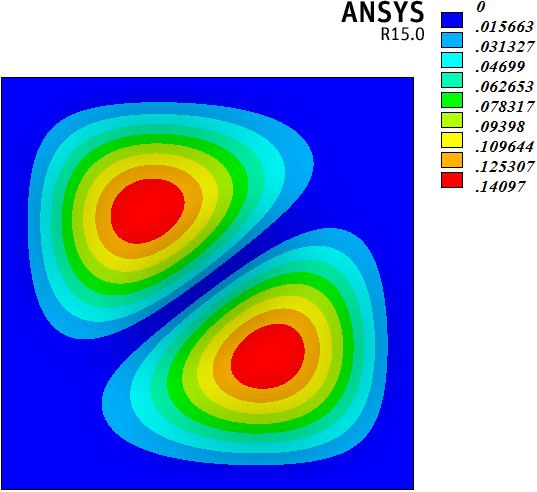
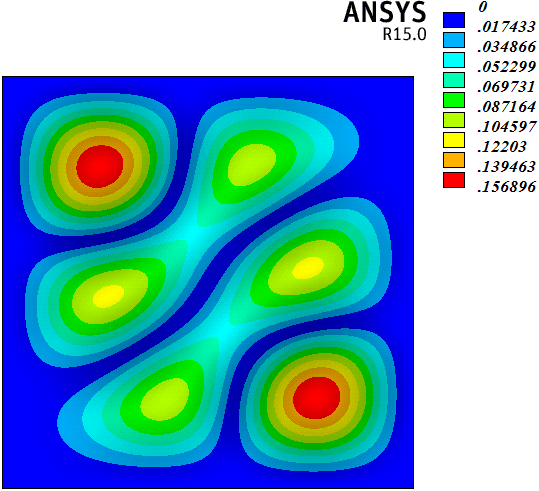
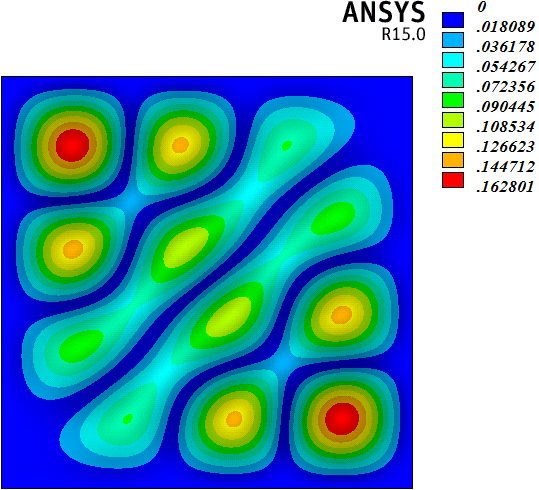
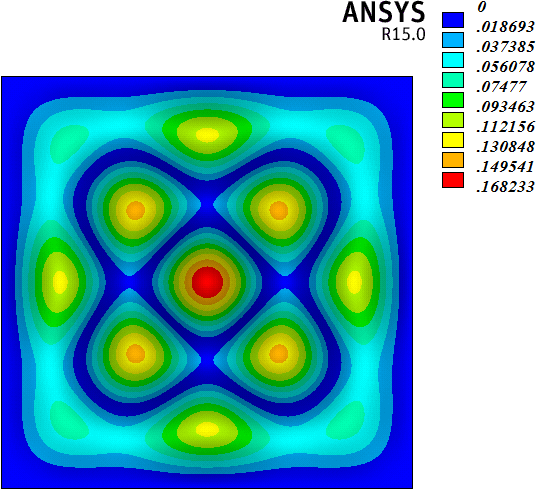
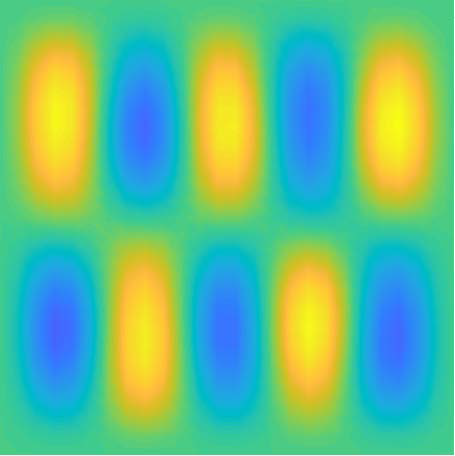
4.3. 振型分析
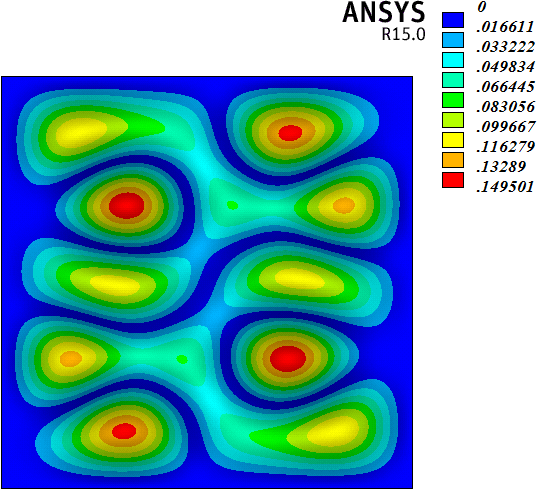
在频率分析的基础上,采用切比雪夫谱方法和有限元方法,研究了算例前25阶频率对应的振型。如图5(1)~图5(25)所示,各子图左侧为切比雪夫谱方法的计算结果,右侧为有限元方法的计算结果。算例1~25阶振型表现出以下规律:1) 切比雪夫谱方法和有限元方法计算的1~25阶振型结果基本规律一致,但不完全相同。两种方法计算的1~7、11~13、16、17、20~22、25阶振型基本相同,8~10、14、15、18、19、23、24振型存在一定差别。2) 差别振型来自重复频率值对应的振型。7阶和8阶、9阶和10阶、14阶和15阶、18阶和19阶、23阶和24阶振型都是重复频率值对应的振型,而且重复频率值对应的振型都是中心对称图形(包括2阶和3阶频率值对应的图形)。采用切比雪夫谱方法和有限元方法计算振型,最明显的差别存在于8阶振型。8阶和7阶振型对应的频率值相同,两种方法计算7阶振型的结果一致,但是两种方法计算得到的8阶振型却不同。这种现象也存在于18阶和19阶振型的计算结果中。实际上,7阶和8阶、18和19阶两对重复频率值对应的振型若采用有限元方法计算,结果是一致的,只是振型图绕中心点旋转了90度。但是7阶和8阶、18和19阶两对重复频率值对应的振型若采用切比雪夫谱方法计算,结果是不一致的。综上所述,在计算四边固支矩形薄板振型时,采用切比雪夫谱方法和有限元方法出现了一些不同的结果,有待进一步研究。

Figure 4. The relationship between frequencies and the number of interpolation points
图4. 频率与插值点数的关系

 (1)
(1)

 (2)
(2)

 (3)
(3)

 (4)
(4)

 (5)
(5)

 (6)
(6)

 (7)
(7)

 (8)
(8)

 (9)
(9)

 (10)
(10)

 (11)
(11)

 (12)
(12)

 (13)
(13)

 (14)
(14)

 (15)
(15)

 (16)
(16)

 (17)
(17)
 (18)
(18)
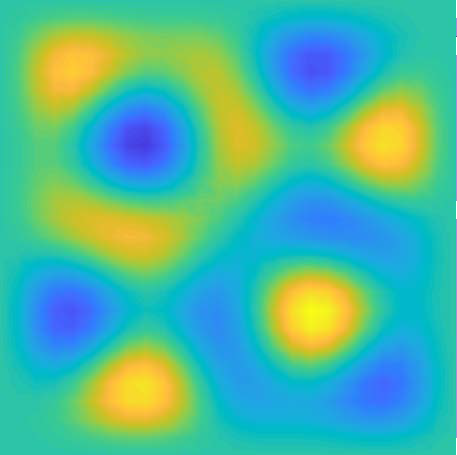
 (19)
(19)

 (20)
(20)

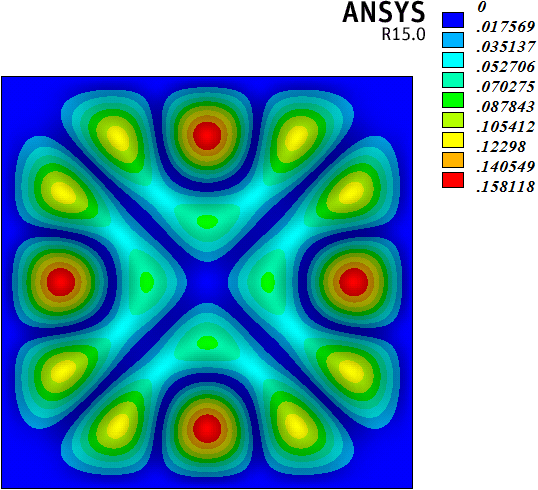 (21)
(21)

 (22)
(22)

 (23)
(23)

 (24)
(24)

 (25)
(25)
Figure 5. Graph of modes
图5. 振型图
5. 结论
本文基于切比雪夫谱方法分析了四边固支矩形薄板的自由振动特性。基于薄板自由振动的位移方程,采用分离变量法推导了薄板自由振动的特征频率方程,建立了薄板各物理参数与自由振动频率之间的关系式。建立了任意区间、任意矩形区域与[−1, 1]区间内切比雪夫插值点的映射关系,构造出满足四边固支矩形薄板自由振动微分方程的高阶求导矩阵,得到了薄板自由振动的特征频率矩阵方程,该方程不含刚度矩阵和质量矩阵。算例薄板前25阶自由振动频率的计算结果表明,切比雪夫谱方法选取25个插值点的计算结果与有限元的计算结果相比,两者最大误差仅有0.31%,切比雪夫谱方法在计算9阶和10阶、24阶和25阶频率时,选取15~25个插值点,计算结果趋于稳定,收敛速度很快。因此本文提出的切比雪夫谱方法具有选取插值点少、收敛速度快、计算精度高的特点。在分析算例薄板的振型时,发现有限元方法与切比雪夫谱方法的计算结果存在某些差别,有待进一步研究。此外,基于切比雪夫谱方法的中厚板、各向异性材料板、不规则形状板以及其他边界条件下板的自由振动特性分析,有待深入研究。
基金项目
国家自然科学基金(11472057),北京信息科技大学“勤信拔尖人才”培育计划项目(QXTCPB201701),北京市自然科学基金(1182010)。
文章引用
赵中凯,张君华,刘彦琦. 基于谱方法的矩形薄板自由振动分析
Free Vibration Analysis of Rectangular Thin Plates Based on Spectral Method[J]. 力学研究, 2019, 08(01): 54-64. https://doi.org/10.12677/IJM.2019.81007
参考文献
- 1. 李东旭. 挠性航天器结构动力学[M]. 北京: 科学出版社, 2010.
- 2. 翟婉明. 车辆—轨道耦和动力学[M]. 第四版. 北京: 科学出版社, 2015.
- 3. Ritz, W. (1909) Theorie der Transversalschwingungen einer quadratischen platte mit freien randern. Annalen der Physik, 333, 737-786. https://doi.org/10.1002/andp.19093330403
- 4. Mindlin, R.D. (1951) Influence of Rotatory Inertia and Shear on Flexural Motion of Isotropic Elastic Plate. Journal of Applied Mechanics, 18, 31-38.
- 5. Gorman, D.J. (1982) Free Vibration Analysis of Rectangular Plates. Elsevier, New York.
- 6. 钟阳, 李锐, 田斌. 四边固支矩形薄板自由振动的哈密顿解析解[J]. 应用力学学报, 2011, 28(4): 323-327.
- 7. Liew, K.M. and Wang, C.M. (1993) pb-2 Rayleigh-Ritz Method for General Plate Analysis. Engineering Structure, 15, 55-60. https://doi.org/10.1016/0141-0296(93)90017-X
- 8. Cheung, Y.K. and Zhou, D. (2002) Three-Dimensional Vibration Analysis of Cantilevered and Completely Free Isosceles Triangular Plates. International Journal of Solid and Structure, 39, 673-687. https://doi.org/10.1016/S0020-7683(01)00196-2
- 9. 陈林, 肖伟, 刘见华, 等. 基于改进傅立叶级数的矩形薄板振动特性分析[J]. 噪声与振动控制, 2018, 38(5): 21-26.
- 10. Silling, S.A. (2000) Reformulation of Elasticity Theory for Discontinuities and Long-Range Forces. Journal of the Mechanics and Physics of Solids, 48, 175-209. https://doi.org/10.1016/S0022-5096(99)00029-0
- 11. Orszag, S.A. (1969) Numerical Methods for the Simulation of Turbulence. Physics of Fluids, 12, 250-257.
- 12. Gottlieb, D. and Orszag, S.A. (1977) Numerical Analysis of Spectral Method: Theory and Applications. Capital City Press, Montpelier. https://doi.org/10.1137/1.9781611970425
- 13. Canuto, C., Hussaini, M.Y., Quarteroni, A. and Zang, T.A. (1988) Spectral Method in Fluid Dynamics. Springer, Berlin. https://doi.org/10.1007/978-3-642-84108-8
- 14. Shen, J., Tang, T. and Wang, L.L. (2011) Spectral Methods: Algorithms, Analysis and Applications. Springer, Berlin. https://doi.org/10.1007/978-3-540-71041-7
- 15. Chen, S. and Shen, J. (2018) Enriched Spectral Methods and Applications to Problems with Weakly Singular Solutions. Journal of Scientific Computing, 77, 1468-1489. https://doi.org/10.1007/s10915-018-0862-z
- 16. Shen, Y.P., Zhu, Z.J., Wang, S.L. and Wang, G. (2019) Dynamic Analysis of Tapered Thin-Walled Beams Using Spectral Finite Element Method. Shock and Vibration, 2019, Article ID 2174209. https://doi.org/10.1155/2019/2174209
- 17. Trefethen, L.N. (1996) Finite Difference and Spectral Method for Ordinary and Partial Differential Equations. Cornell University, Ithaca, New York.
- 18. 刑誉峰, 刘波. 板壳自由振动的精确解[M]. 北京: 科学出版社, 2015.
- 19. Fox, L. and Parker, I.B. (1968) Chebyshev Polynomials in Numerical Analysis. Oxford University Press, Oxford.
- 20. Steeb, W. and Hardy, Y. (2006) Problems and Solutions in Introductory and Advanced Matrix Calculus. World Scientific Publishing Company, Singapore. https://doi.org/10.1142/6202
