Pure Mathematics
Vol.4 No.04(2014), Article
ID:13888,6
pages
DOI:10.12677/PM.2014.44022
The Gerber-Shiu Discounted Penalty Function for the Risk Model with Phase-Type Inter Claim Times
School of Mathematics and Computer Science, Shanxi Normal University, Linfen
Email: xiaojuxia2426@126.com
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jun. 12th, 2014; revised: Jul. 10th, 2014; accepted: Jul. 17th, 2014
ABSTRACT
Research in the phase-type distribution has an important influence for the research of other distributions on the positive real axis. It considers the risk model with the phase-type inter-claim times and for constant interest, it first derives the integral-differential equation satisfied by the Gerber-Shiu discounted penalty function. Then through a series of deriving, it obtains the volterra integral equation in a form of matrix. It gets a method of solving the Gerber-Shiu expected penalty function.
Keywords
Phase-Type Inter-Claim Times, Constant, Integral Function, Differential Equation, Volterra

带常利率的时间间隔为相位的Gerber-Shiu折现罚金函数
肖菊霞
山西师范大学数学与计算机科学学院,临汾
Email: xiaojuxia2426@126.com
收稿日期:2014年6月12日;修回日期:2014年7月10日;录用日期:2014年7月17日

摘 要
相位分布的研究在研究正半轴的其他分布中起着重要作用。考虑带常利率的时间间隔为相位分布的更新风险模型。首先推导出Gerber-Shiu期望折现罚金函数满足的积分微分方程,然后经过一系列的推导过程得到Volterra形式的矩阵积分方程,从而得到Gerber-Shiu期望折现罚金函数的一种解法。
关键词
时间间隔为相位分布,常利率,积分方程,微分方程,Volterra

1. 引言
带常利率的更新风险模型,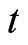 时刻资产余额
时刻资产余额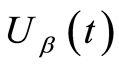 的微分方程形式为
的微分方程形式为
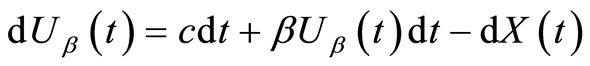 ,
,
其中常数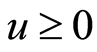 表示初始准备金,常数
表示初始准备金,常数 表示保费率,常数
表示保费率,常数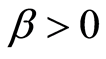 表示常利息力。
表示常利息力。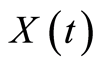 表示
表示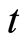 时刻为止的总索赔额,更新过程
时刻为止的总索赔额,更新过程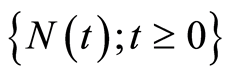 表示
表示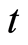 时刻为止的总索赔次数;索赔额
时刻为止的总索赔次数;索赔额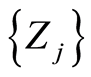 是分布为
是分布为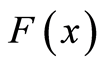 ,密度为
,密度为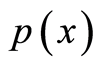 的独立同分布随机变量;
的独立同分布随机变量;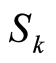 表示第
表示第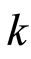 次索赔发生时刻,其中
次索赔发生时刻,其中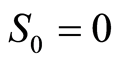 ;索赔时间间隔
;索赔时间间隔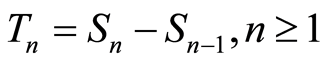 是独立同分布的正随机变量,其分布函数
是独立同分布的正随机变量,其分布函数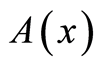 ,密度函数
,密度函数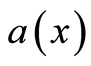 。则
。则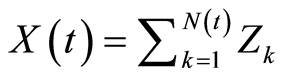 。
。
当初始余额为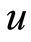 时,破产时刻
时,破产时刻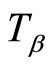 定义为:
定义为:
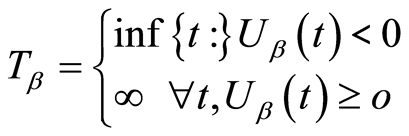
若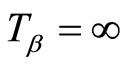 ,则表示破产没有发生;若有破产发生,则破产前瞬间资产余额为
,则表示破产没有发生;若有破产发生,则破产前瞬间资产余额为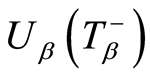 ,破产时赤字为
,破产时赤字为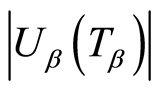 ,期望折现函数是破产前瞬间资产余额和破产时赤字的期望折现,当初始余额为
,期望折现函数是破产前瞬间资产余额和破产时赤字的期望折现,当初始余额为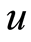 时,定义为:
时,定义为:

其中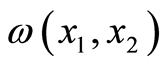 是破产前瞬间资产余额和破产时赤字的非负罚金函数,折现因子
是破产前瞬间资产余额和破产时赤字的非负罚金函数,折现因子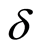 是非负参数,
是非负参数,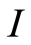 是示性函数。
是示性函数。
相位分布是在风险理论中最常见的分布之一,近年来人们越来越关注时间间隔为为相位分布的Sparre Andersen模型。例如[Albrecher and Boxma] (2005)通过Laplace-Stieltjes变换分析折现罚金函数,[Dickson and Drekic] (2004), [Jiandong Ren] (2008)[1] 考虑了研究了破产前瞬间资产余额和破产时赤字的联合分布函数,又如[Mogens Bladt] (2005)[2] 研究了相位分布的应用。
对Gerber-Shiu折现罚金函数的研究是破产理论主要研究的问题之一。对此问题的研究始于[Gerber and Shiu] (1998)[3] ; [Dickson and Hipp] (1998), [Lin] (2003)研究了时间间隔为Erlang (2), [Rong Wu, Yuhua Lu, and Ying Fang] (2007)[4] 研究了时间间隔为相位分布。
常利息力更新风险模型也是现代风险理论研究的重要方面, 许多人都做过这方面的工作。例如[Sundt and Teugels] (1997), [Yang and Zhang] (1997), [Cai] (2002)[5] , [Cardoso and Waters] (2003)。
本文考虑带常利率的时间间隔为相位分布的更新风险模型。首先推导出Gerber-Shiu期望折现罚金函数满足的积分微分方程,然后经过一系列的推导过程得到Volterra形式的矩阵积分方程,从而得到Gerber-Shiu期望折现罚金函数的一种解法。
2. 相位分布简介
假定索赔时间间隔的分布 是参数为
是参数为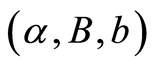 的相位分布,连续时间马氏链
的相位分布,连续时间马氏链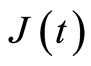 有
有 个暂态
个暂态 和一个吸收态
和一个吸收态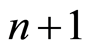 。其中
。其中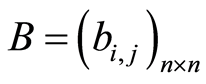 ,
,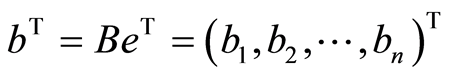 ,
,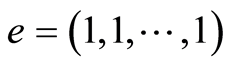 ,
,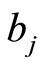 ,
,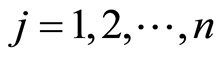 是从暂态
是从暂态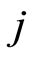 跳到吸收态的密度,
跳到吸收态的密度,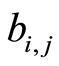 ,
,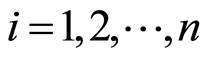 。
。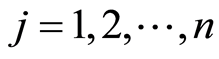 是从暂态
是从暂态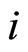 跳到暂态
跳到暂态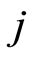 的密度,
的密度,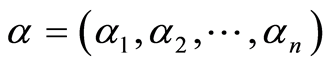 是初始分布概率,其中
是初始分布概率,其中 ,
,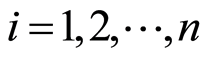 ,
, 。
。
对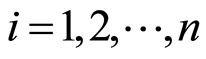 ,
,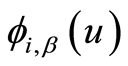 是初值为
是初值为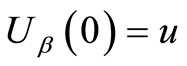 ,初始状态
,初始状态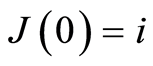 的期望罚金折现函数,定义为:
的期望罚金折现函数,定义为:
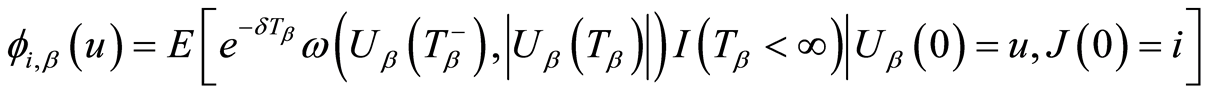 (1)
(1)
若记
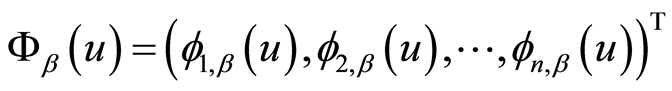 (2)
(2)
则期望折现罚金函数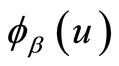 可由下式给出:
可由下式给出:
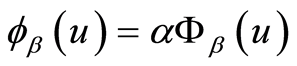 (3)
(3)
3. 主要结论
定理2.1 对任意的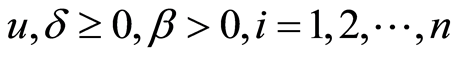

证明:考虑在足够小的时间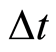 内,由相位分布的性质,在此时间段内最多发生一次状态改变(暂态之间变化)或发生一次索赔,而且状态改变与索赔不可能同时发生,故
内,由相位分布的性质,在此时间段内最多发生一次状态改变(暂态之间变化)或发生一次索赔,而且状态改变与索赔不可能同时发生,故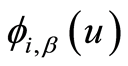 可在下面三种情况下取得1)在时间
可在下面三种情况下取得1)在时间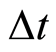 内没有发生索赔及状态改变;2)在时间
内没有发生索赔及状态改变;2)在时间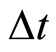 内没有发生索赔但发生状态改变;3)在时间
内没有发生索赔但发生状态改变;3)在时间 内发生
内发生
一次索赔,索赔后可能导致破产也可能没有破产,当索赔额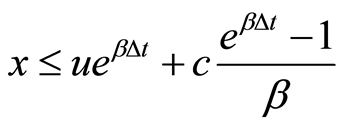 时,表示没有破产,当
时,表示没有破产,当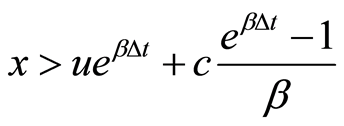 时,表示破产发生。
时,表示破产发生。
由以上及(1)式可知:
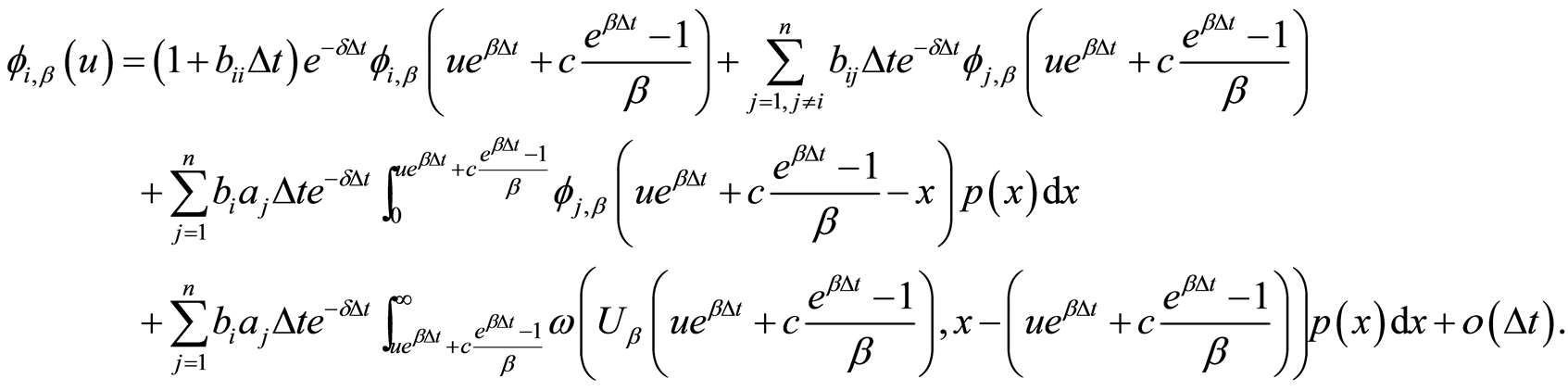 (4)
(4)
因为
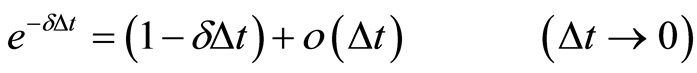
所以(4)式为
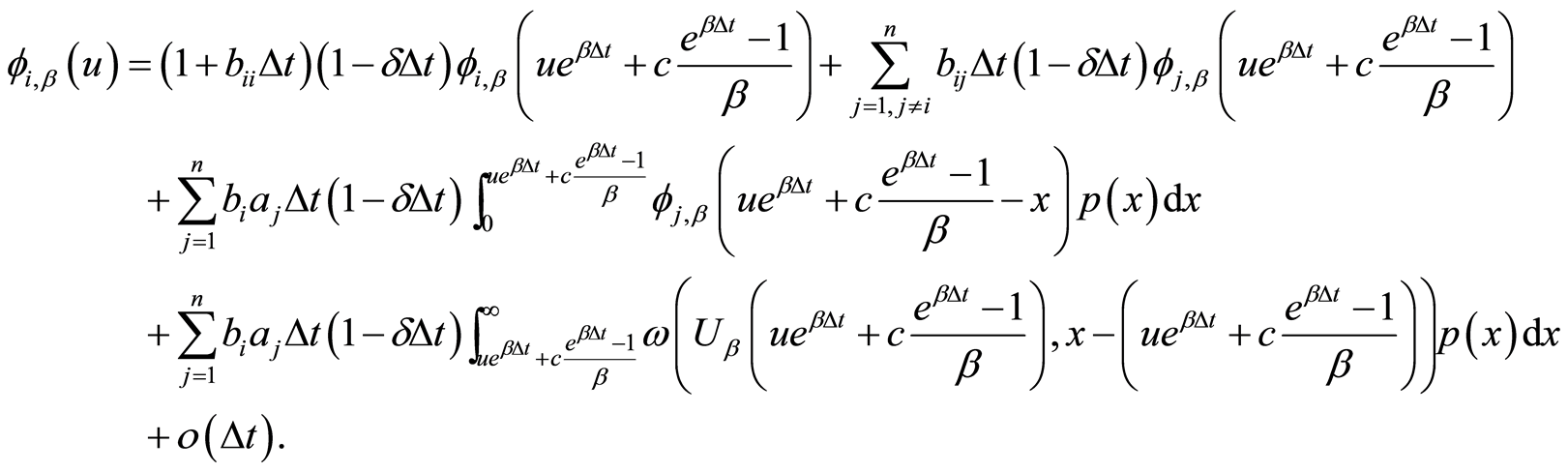 (5)
(5)
移项整理(5)且等式两端同除 得:
得:
 (6)
(6)
在(6)中,令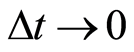 ,且由
,且由
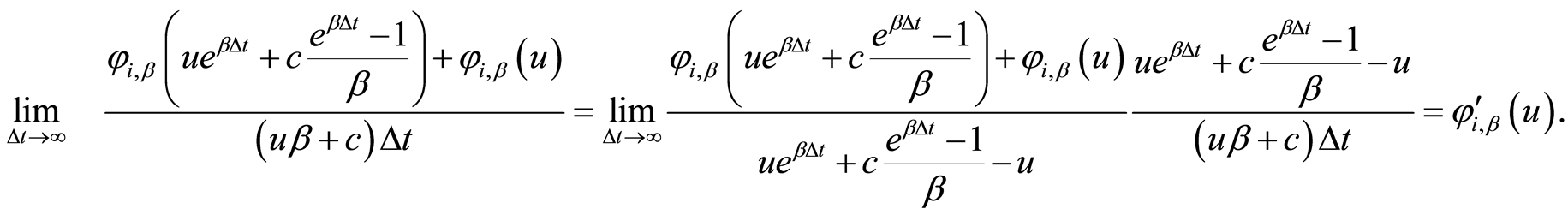
可得:
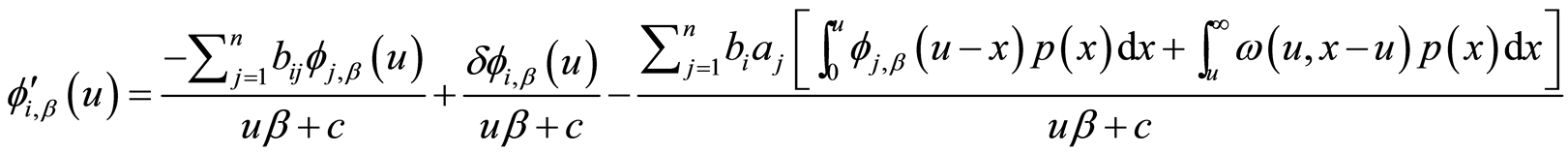
推论2.1 对任意的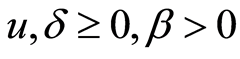
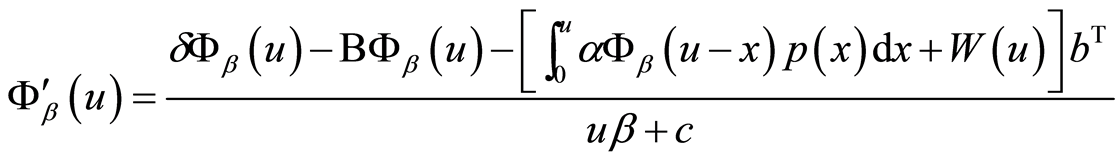 (7)
(7)
其中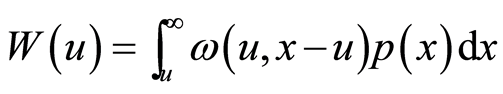 。
。
证明:由(2)(4)及相位初始分布的性质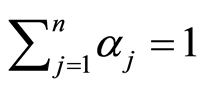 直接推出。
直接推出。
定理2.2 对任意的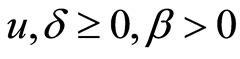
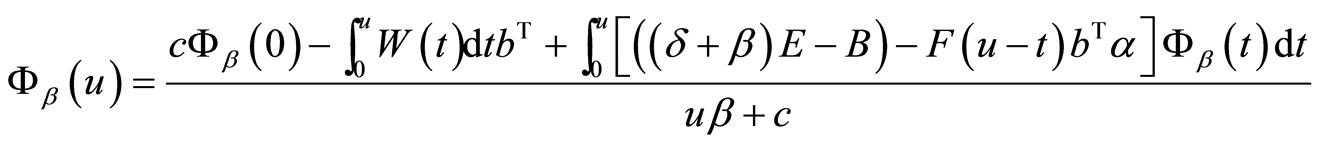 (8)
(8)
其中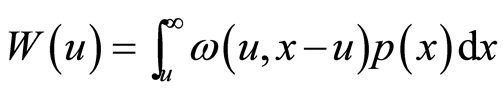 。
。
证明:(7)式两边同乘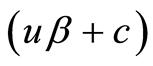 ,得到
,得到
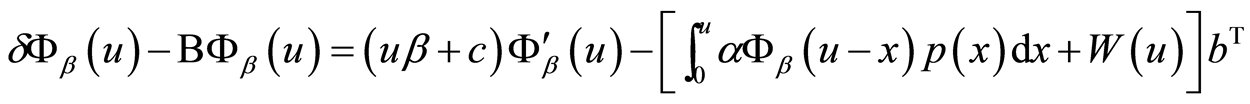
整理得
 (9)
(9)
用 替换
替换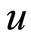 (9)式变为
(9)式变为
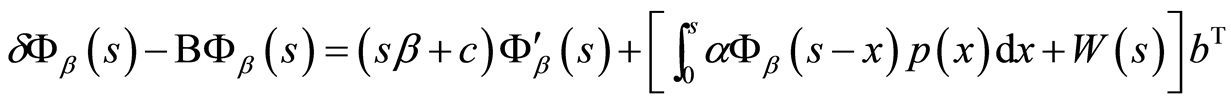 (10)
(10)
(10)式两端对变量s作积分,有

若记E为n阶单位矩阵,由分部积分法及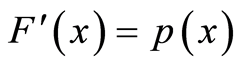 ,得
,得
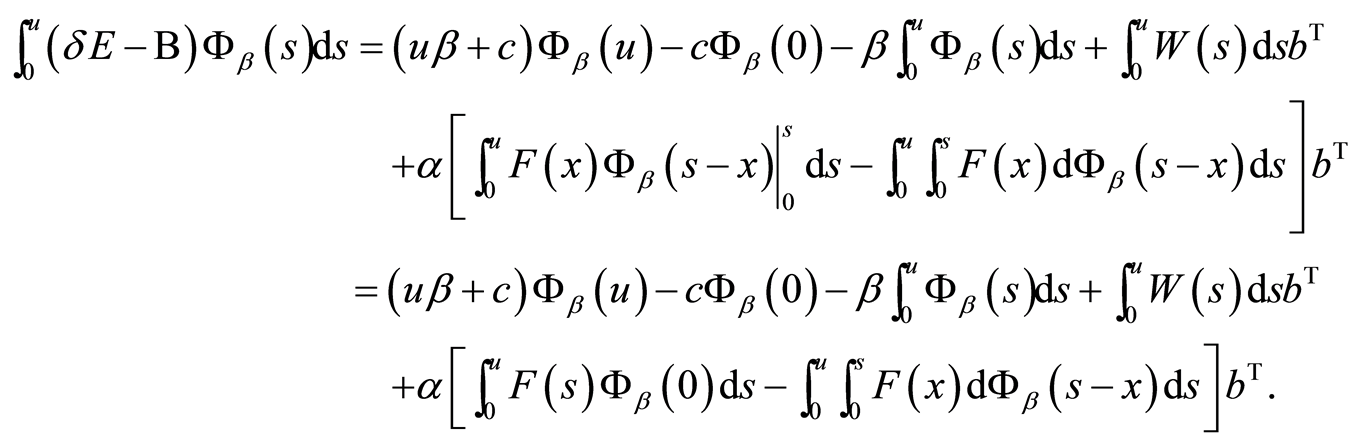 (11)
(11)
而
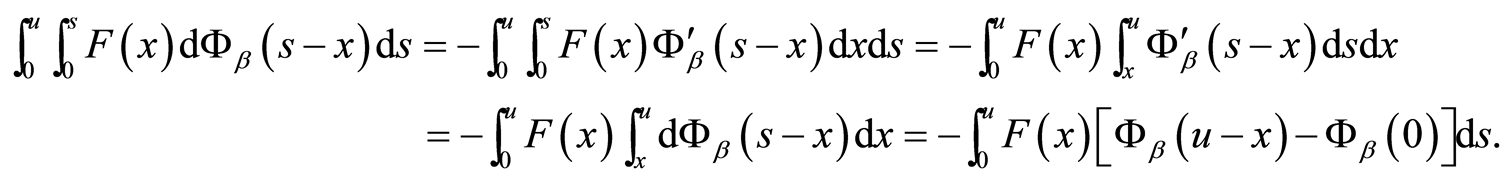
故而(11)式为
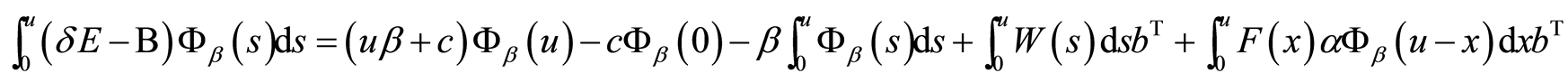
故而
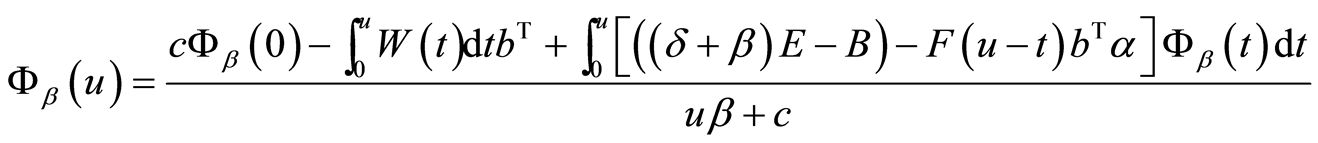
引理2.1
若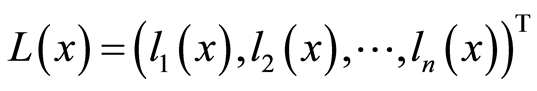 是向量函数,且
是向量函数,且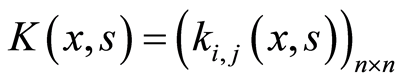 是Volterra核矩阵,即
是Volterra核矩阵,即
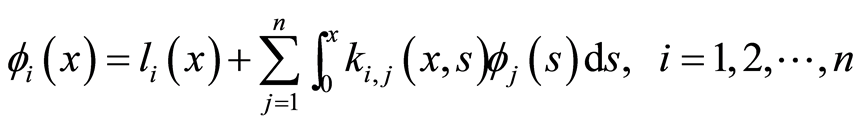
其中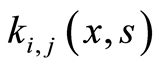 是
是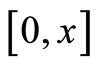 上的
上的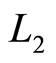 可积函数,则对任意的
可积函数,则对任意的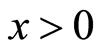 ,
,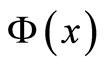 的解可以表示为:
的解可以表示为:

其中
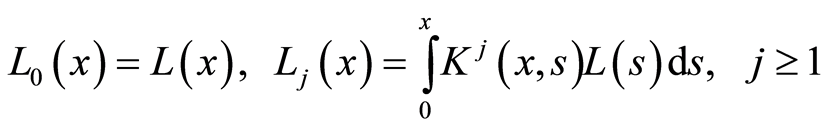
 是迭核,按方阵的乘积处理。
是迭核,按方阵的乘积处理。
注:引自参考文献[6] 。
定理2.3 对任意的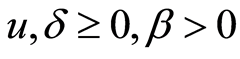
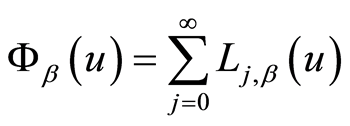 (12)
(12)
其中
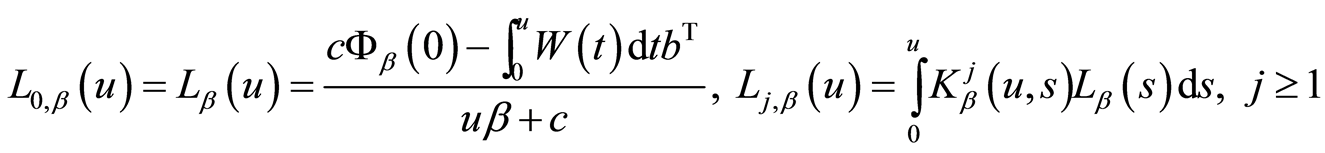
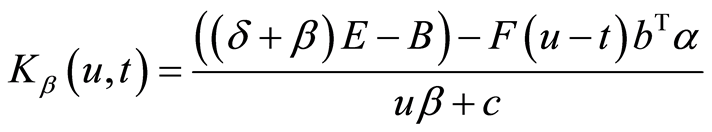
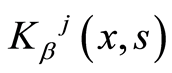 以方阵的乘积处理,
以方阵的乘积处理,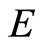 为
为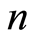 阶单位阵。
阶单位阵。
证明:(8)式为Volterra积分方程组形式
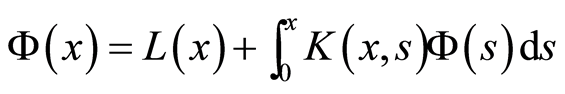
由于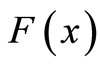 可微,故
可微,故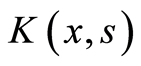 是
是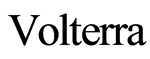
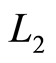 核矩阵,从而由引理2.1可得结论。
核矩阵,从而由引理2.1可得结论。
4. 结论与建议
由(12)可知,只需求出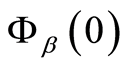 便可得出
便可得出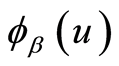 ,再由
,再由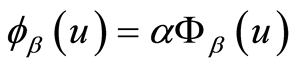 可求出期望惩罚函数
可求出期望惩罚函数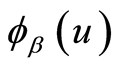 。
。
在定理2.2中令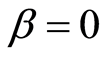 ,可得Volterra积分方程组形式
,可得Volterra积分方程组形式

在定理2.3中取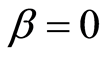 ,则有
,则有
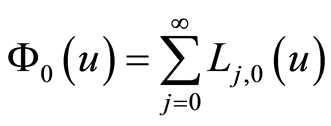
其中
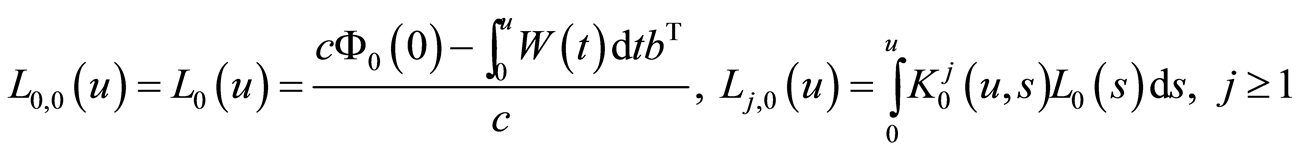
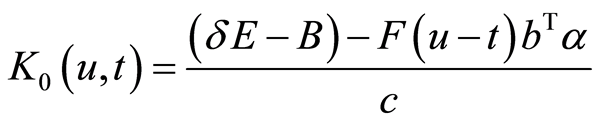
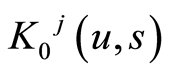 以方阵的乘积处理,
以方阵的乘积处理,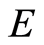 为
为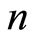 阶单位阵。
阶单位阵。
由以上推导可知,只要求出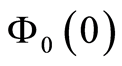 ,就可求出
,就可求出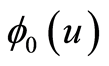 ,进而可求出
,进而可求出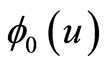 。
。
参考文献 (References)
- Ren, J.D. (2008) The discounted joint distribution of surplus prior to ruin and the deficit at ruin in a sparre andersen model. North American Actuarial Journal, 11, 128-136.
- Bladt, M. (2005) A review on phase-type distributions and their use in risk theory. Astin Bulletin, 35, 145-161.
- Gerber, H.U. and Shiu, E.S.W. (1998) On the time value of ruin. North American Actuarial Journal, 2, 48-72.
- Wu, R., Lu, Y.H. and Fang, Y. (2007) On the Gerber-Shiu discounted penalty function for the ordinary renewal risk model with constant interest. North American Actuarial Journal, 11, 135.
- Cai, J. and Dickson, D.C.M. (2002) On the expected discounted penalty function at ruin of a surplus process with interest. Insurance: Mathematics and Economics, 30, 389-404.
- 《现代应用数学手册》编委会 (2006) 现代应用数学手册, 分析与方程卷. 清华大学出版社, 北京, 921-963.