Pure Mathematics
Vol.05 No.02(2015), Article ID:14936,6
pages
10.12677/PM.2015.52011
A New Construction for Inverse Semigroups
Shanshan Liu, Junying Guo, Xiaojiang Guo
College of Mathematics and Information Science, Jiangxi Normal University, Nanchang Jiangxi
Email: liushanshan199008@126.com, 651945171@qq.com, xjguo@jxnu.edu.cn
Received: Feb. 26th, 2015; accepted: Mar. 8th, 2015; published: Mar. 12th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Thenotion of FC-system is introduced. In this note, a new construction for inverse semigroups is established in terms of Munn semigroups and Clifford semigroups.
Keywords:Fundamental Inverse Semigroup, Clifford Semigroup, Inverse Semigroup
逆半群的一新构造
刘姗姗,郭俊颖,郭小江
江西师范大学数学与信息科学学院,江西 南昌
Email: liushanshan199008@126.com, 651945171@qq.com, xjguo@jxnu.edu.cn
收稿日期:2015年2月26日;录用日期:2015年3月8日;发布日期:2015年3月12日

摘 要
本文定义FC-系统的概念。从这一概念出发,利用Munn半群和Clifford半群建立了逆半群的一新结构。
关键词 :基本逆半群,Clifford半群,逆半群

1. 引言
逆半群是每个元素都只有一个逆元的正则半群。等价地,正则半群是逆半群当且仅当其幂等元集构成交换子半群。这类半群是离群最近的半群类之一,具有许多“群类似”性质,在半群理论研究中具有重要地位,也有非常丰富的研究成果(见[1] [2] )。
逆半群有两类重要子类:一类是Clifford半群。所谓Clifford半群是具有中心幂等元的正则半群。这类半群可以表示为一些群的半格。
另一类是基本逆半群(fundanmental inverse semigroup)。令 为逆半群,
为逆半群, 为
为 的幂等元集。
的幂等元集。 上的同余
上的同余 称为幂等元分离同余,如果
称为幂等元分离同余,如果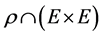 是
是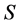 上的恒等映射。我们用H,L,R,D,J记通常的Green-关系。众所周知,
上的恒等映射。我们用H,L,R,D,J记通常的Green-关系。众所周知, 是
是 上的幂等元分离同余当且仅当
上的幂等元分离同余当且仅当 。记
。记 为
为 上的最大幂等元分离同余。逆半群称为基本逆半群,如果其最大幂等元分离同余为恒等映射。更有意思的是,
上的最大幂等元分离同余。逆半群称为基本逆半群,如果其最大幂等元分离同余为恒等映射。更有意思的是, 是基本逆半群。这说明,任一逆半群都是以基本逆半群作为同态像。特别地,Munn指出:一个半群是基本逆半群当且仅当它同构于某个Munn半群
是基本逆半群。这说明,任一逆半群都是以基本逆半群作为同态像。特别地,Munn指出:一个半群是基本逆半群当且仅当它同构于某个Munn半群 的全子逆半群(可见,[3] )。
的全子逆半群(可见,[3] )。
Clifford半群和基本逆半群都具有简明结构。能否从基本逆半群(Munn半群)出发构造逆半群?这是一个非常自然的问题。受到文献[4] [5] 鼓励,本文将给出逆半群基于Munn逆半群和Clifford半群的一种构造方法。
2. 定理
令 为逆半群,记
为逆半群,记 为
为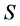 的幂等元集。若
的幂等元集。若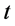 为
为 的元,则我们用
的元,则我们用 记
记 的逆元。设
的逆元。设
 :半格;
:半格;
 :以半格
:以半格 为幂等元集的基本逆半群;
为幂等元集的基本逆半群;
 :以半格
:以半格 为幂等元集的Clifford半群;
为幂等元集的Clifford半群;
进一步,设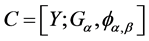 是Clifford半群
是Clifford半群 分解成群
分解成群 的半格分解。记
的半格分解。记 为
为 到自身的半群同态半群。定义
到自身的半群同态半群。定义

其中 ,且
,且
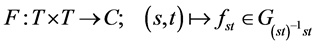
定义2.1:五元组 称为
称为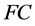 -系统,如果
-系统,如果
(I1) 对于任意 ,有
,有 ;
;
(I2) 对于任意 ,有
,有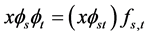 ;
;
(I3) 对于任意 ;
;
(I4) 对于任意 ;
;
(I5) 对于任意 
任给 -系统
-系统 ,构作集合
,构作集合

在集合 上,定义
上,定义

注意到, ,易知,
,易知, ,于是
,于是 ,从而
,从而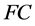 关于运算
关于运算 封闭。进而,
封闭。进而, 为逆半群。
为逆半群。
下面是本文的主要结果。
定理2.2:令 为
为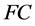 -系统,则
-系统,则 是逆半群。反过来,任一逆半群均可以这样构作。
是逆半群。反过来,任一逆半群均可以这样构作。
3. 定理证明
本节我们给出定理2.2的证明。
引理3.1:令 为
为 -系统,则
-系统,则 是逆半群。
是逆半群。
证明:对于 ,我们有
,我们有

于是 为半群。
为半群。
若 ,则
,则 。反之,若
。反之,若 为幂等元,则
为幂等元,则 ,于是
,于是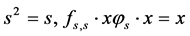 。由前一等式,可知
。由前一等式,可知 ,再结合后一等式,
,再结合后一等式, ,从而
,从而 。故
。故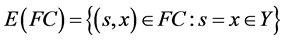 。通常验算,可知
。通常验算,可知 为半格。
为半格。
最后,证明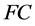 为正则半群。这可由下面的计算得到:
为正则半群。这可由下面的计算得到:
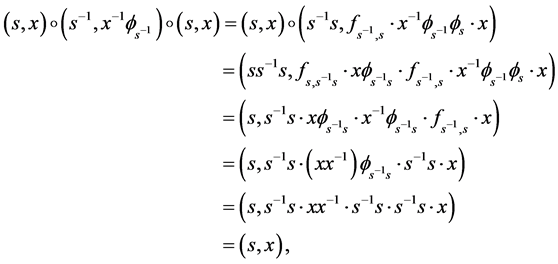
为方便记,以下总假设 是以
是以 为幂等元半格的逆半群,
为幂等元半格的逆半群, 为
为 上的最大幂等元分离同余。记
上的最大幂等元分离同余。记 。
。
引理3.2:(1)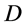 是
是 的以
的以 为幂等元集的Clifford子半群。
为幂等元集的Clifford子半群。
(2) 对于任意的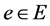 ,
,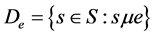 是以
是以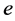 为单位元的
为单位元的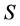 的子群。
的子群。
(3) 是
是 的半格分解。
的半格分解。
证明:由Lellament引理,知正则半群上的所有同态都是幂等元提升的,于是 为
为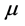 的核,即
的核,即
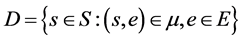 ,而
,而 为半格,从而
为半格,从而 是以
是以 为幂等元集的
为幂等元集的 的子半群。
的子半群。
令 ,则存在
,则存在 ,使得
,使得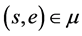 ,于是
,于是 ,即
,即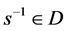 ,从而
,从而 为正则半群。
为正则半群。
因此 为逆半群。而
为逆半群。而 ,则
,则 ,进而
,进而 为群并(union of groups)。
为群并(union of groups)。
但可以表示一些子群并的逆半群是Clifford半群,故 为Clifford半群。
为Clifford半群。
对于 ,由于
,由于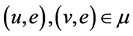 ,有
,有 ,于是
,于是 ;类似地,
;类似地, 。由上
。由上
一段的证明,知 ,从而
,从而 是以
是以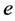 为单位元的子群。
为单位元的子群。
注意到,若 ,则
,则 ,于是
,于是 。故
。故 是Clifford半群
是Clifford半群 的半格分解。
的半格分解。
记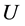 为
为 关于同余
关于同余 分类的代表元集。由于
分类的代表元集。由于 为幂等元分离同余,所以幂等元所在
为幂等元分离同余,所以幂等元所在 -类仅含一个元素,故
-类仅含一个元素,故 。在
。在 上,定义如下运算:
上,定义如下运算:

其中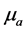 表示
表示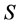 的包含
的包含 的
的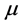 -类。易知,
-类。易知, 为半群,且同构于
为半群,且同构于 ,于是
,于是 是以
是以 为幂等元集的基本逆半群。
为幂等元集的基本逆半群。
引理3.3:对于任意的 ,存在惟一
,存在惟一 使得
使得 且
且 。
。
证明:据 的定义,有
的定义,有 使得
使得 。显然,
。显然,

据 为幂等元分离同余,
为幂等元分离同余, 且
且 ,于是
,于是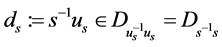 。进而
。进而
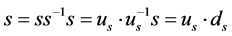
现假设 满足
满足 的条件。因为
的条件。因为 ,所以
,所以 ,而
,而 是代表元集,于是
是代表元集,于是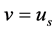 。注意到,
。注意到, 。从而
。从而 。这样,
。这样, 的惟一性获证。
的惟一性获证。
对于 ,由引理3.3,知
,由引理3.3,知 。由于
。由于 ,我们知,
,我们知, ,但
,但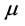 为幂等元分离同余,于是
为幂等元分离同余,于是 。规定
。规定

另一方面,对于 ,我们有
,我们有 ,再据引理3.3,有
,再据引理3.3,有 。定义
。定义

显然,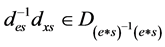 。而
。而 ,我们有
,我们有

这意味着, 。
。
引理3.4: 是
是 的自同态。
的自同态。
证明:注意到,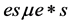 。我们有
。我们有 ,但
,但 ,于是
,于是 。令
。令 。据
。据 的定义,知
的定义,知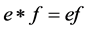 ,进而
,进而
 (1)
(1)
而

且 ,利用等式(1),我们有
,利用等式(1),我们有
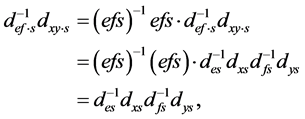
即 。从而
。从而 为半群同态。
为半群同态。
定义映射
引理3.5:五元组 是
是 -系统。
-系统。
证明:仅需证明, 满足条件(I1)~(I5)。令
满足条件(I1)~(I5)。令 。记
。记 。
。
据引理3.4的证明, ,进而
,进而

但 ,再利用引理3.3,有
,再利用引理3.3,有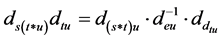 ,即
,即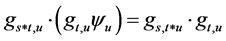 。这意味着,(I1)满足。
。这意味着,(I1)满足。
现设 ,记
,记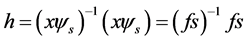 ,则
,则
 (2)
(2)
但

且 ,于是
,于是

即(I2)成立。
对于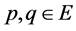 ,由定义,有
,由定义,有 ,显然
,显然 ,再据引理3.3,我们有
,再据引理3.3,我们有 ,从而
,从而 。我们证明了(I3)。
。我们证明了(I3)。
注意到, 。因为
。因为 为Clifford半群,所以
为Clifford半群,所以 ,且
,且 ,从而由引理3.3,知
,从而由引理3.3,知 。而由(I3),有
。而由(I3),有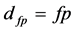 ,进而
,进而 。故
。故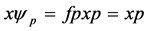 ,这样条件(I4)得证。
,这样条件(I4)得证。
最后,由 ,利用引理3.3,有
,利用引理3.3,有 ,即
,即 。从而完成证明。
。从而完成证明。
定义
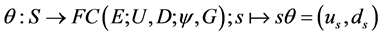
由引理3.3, 是单射。为证明定理2.2,仅需证明:
是单射。为证明定理2.2,仅需证明: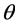 是半群同构。
是半群同构。
引理3.6: 是半群同构。
是半群同构。
证明:令 ,由引理3.3,
,由引理3.3, ,进而
,进而

再结合

利用引理3.3,有 ,于是
,于是

从而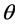 是半群同态。
是半群同态。
对于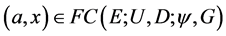 ,则
,则 。由引理3.3,有
。由引理3.3,有 ,进而
,进而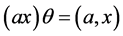 ,于是
,于是 为满射。从而
为满射。从而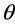 为半群同态。
为半群同态。
基金项目
国家自然科学基金(11361027),江西省自然科学基金和江西省教育厅科研基金资助项目。
文章引用
刘姗姗,郭俊颖,郭小江, (2015) 逆半群的一新构造
A New Construction for Inverse Semigroups. 理论数学,02,73-79. doi: 10.12677/PM.2015.52011
参考文献 (References)
- 1. Guo, X.J., Ren, C.C. and Shum, K.P. (2007) Dual wreath product structure of right C-rpp semigroups. Algebra Collo-quium, 14, 285-294.
- 2. Guo, X.J., Zhao, M. and Shum, K.P. (2008) Wreath product structure of left C-rpp semi-groups. Algebra Colloquium, 15, 101-108.
- 3. Howie, J.M. (1976) An introduction to semigroup theory. Academic Press, London.
- 4. Lawson, M.V. (1998) Inverse semigroups. World Scientific, Singapore, New Jersey, Hong Kong.
- 5. Petrich, M. (1984) Inverse semigroups. John Wiley & Sons, Inc., New York.