Pure Mathematics
Vol.06 No.05(2016), Article ID:18624,8
pages
10.12677/PM.2016.65060
Gradient Estimates for Quasilinear Elliptic p-Laplacean Equations
Moqin Wang
College of Science, Shanghai University, Shanghai

Received: Sep. 9th, 2016; accepted: Sep. 23rd, 2016; published: Sep. 28th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper we obtain the pointwise gradient estimates via the non-linear Wolff potentials for weak solutions of the non-homogeneous quasilinear elliptic p-Laplacean equations with measure data.
Keywords:p-Laplacean, Quasilinear, Elliptic, Wolff Potential, Gradient Estimate

拟线性p-调和型椭圆方程的梯度估计
王墨琴
上海大学理学院,上海

收稿日期:2016年9月9日;录用日期:2016年9月23日;发布日期:2016年9月28日

摘 要
本文我们利用非线性Wolff位势来研究右端项含测度的非齐次拟线性p-调和型椭圆方程弱解的点态梯度估计。
关键词 :p-调和型,拟线性,椭圆,Wolff位势,梯度估计

1. 引言
本文我们主要考虑下述非齐次拟线性p-调和型椭圆方程
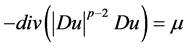 。 (1.1)
。 (1.1)
这里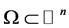 为有界开区域且
为有界开区域且 为Borel测度。
为Borel测度。
1983年,Wolff在文献 [1] 中提出了经典非线性Wolff位势。后来,Kilpeläinen,Malý [2] [3] ,Trudinger,Wang [4] 和Korte,Kuusi [5] 用不同的方法研究了拟线性椭圆方程(1.1)弱解的逐点估计
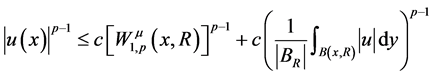 。
。
这里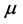 的非线性Wolff位势
的非线性Wolff位势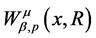 的定义如下:
的定义如下:
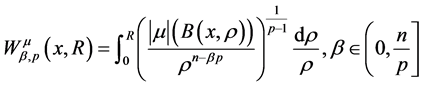 且
且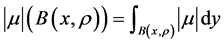 。
。
最近,Duzaar,Kuusi和Mingione在 [6] - [9] 中借助非线性Wolff位势和线性Riesz位势给出了拟线性椭圆方程(1.1)及其一般情形的弱解的逐点梯度估计。本文我们主要采用非线性Wolff位势来研究非齐次p-Laplacean方程(1.1)弱解的梯度估计,我们将结合文 [6] - [9] 的证明方法给出一个新证明。
首先,我们给出弱解的定义。若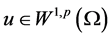 为方程(1.1)的弱解,则对任意
为方程(1.1)的弱解,则对任意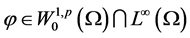 ,有
,有
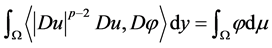 。
。
现在我们来阐述本文的主要结论。
定理1.1. 设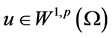 是方程(1.1)的弱解,
是方程(1.1)的弱解, ,
,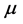 为Borel测度,且
为Borel测度,且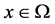 是
是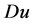 的一个Lebesgue点,
的一个Lebesgue点,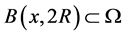 。那么存在
。那么存在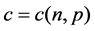 ,有如下梯度估计
,有如下梯度估计
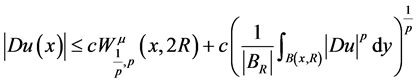 。 (1.2)
。 (1.2)
2. 主要结论的证明
我们记
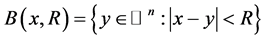 。
。
简记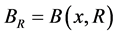 。对具有正测度的集合
。对具有正测度的集合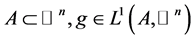 ,记积分平均
,记积分平均
 。
。
引入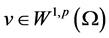 为下述参考方程的弱解
为下述参考方程的弱解
 。 (2.1)
。 (2.1)
现在我们给出齐次p-Laplacean椭圆方程(2.1)弱解的一个经典的估计(参见文献 [10] - [14] )。
定理2.1. 设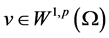 是(2.1)的弱解,则存在
是(2.1)的弱解,则存在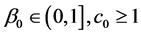 ,它们都依赖于
,它们都依赖于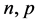 ,有如下估计
,有如下估计
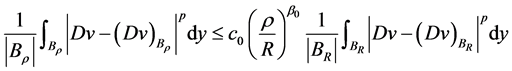 。 (2.2)
。 (2.2)
其中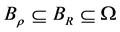 为同心球。
为同心球。
现在考虑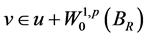 是如下Dirichlet问题的弱解
是如下Dirichlet问题的弱解
 (2.3)
(2.3)
那么,我们可以得到下面的比较引理。
引理2.2. 设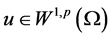 是方程(1.1)的弱解,
是方程(1.1)的弱解,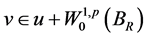 是方程(2.3)的弱解,则存在
是方程(2.3)的弱解,则存在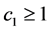 依赖于
依赖于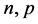 ,当
,当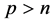 时,有估计
时,有估计
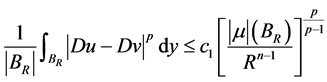 。 (2.4)
。 (2.4)
证明:我们可以通过逼近理论(见 [15] - [17] )只研究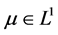 的情形。通过基本的尺度变换
的情形。通过基本的尺度变换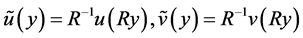 且
且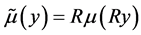
另外,通过归一化变换
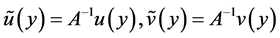 且
且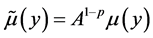 。
。
这里
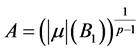 。(2.5)
。(2.5)
我们不妨假设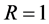 且
且 。故我们只需证明
。故我们只需证明
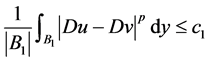 。 (2.6)
。 (2.6)
首先,由弱解的定义可得
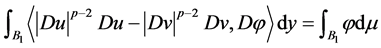 , (2.7)
, (2.7)
对任意 ,任意
,任意 和
和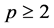 ,我们回顾以下基本不等式
,我们回顾以下基本不等式
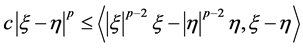 。 (2.8)
。 (2.8)
因为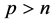 且
且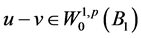 ,那么由Sobolev嵌入定理可得
,那么由Sobolev嵌入定理可得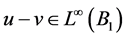 。那么取检验函数
。那么取检验函数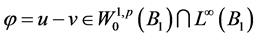 ,由(2.7)式,(2.8)式,Sobolev嵌入定理以及
,由(2.7)式,(2.8)式,Sobolev嵌入定理以及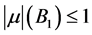 ,可知
,可知
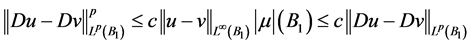 。
。
故,可得(2.6)式,所以结论得证。
下面我们记
 。
。
令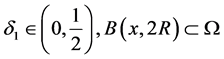 。定义
。定义
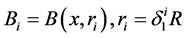 , (2.9)
, (2.9)
其中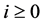 为整数。我们选取
为整数。我们选取
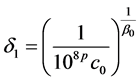 。 (2.10)
。 (2.10)
这里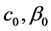 如定理2.1中的定义。
如定理2.1中的定义。
考虑 是下述Dirichlet问题的弱解
是下述Dirichlet问题的弱解
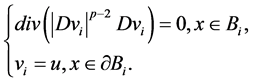 (2.11)
(2.11)
下面我们给出一个迭代引理。
引理2.3. 设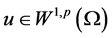 是方程(1.1)的弱解,
是方程(1.1)的弱解,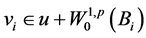 是方程(2.11)的弱解,则有下式成立
是方程(2.11)的弱解,则有下式成立
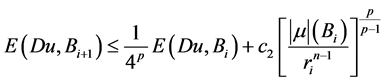 。
。
这里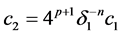 。
。
证明:由定理2.1中的(2.2)式和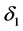 的定义式(2.10)式,可知
的定义式(2.10)式,可知
 。
。
再由引理2.2的(2.4)式和Hölder不等式,有
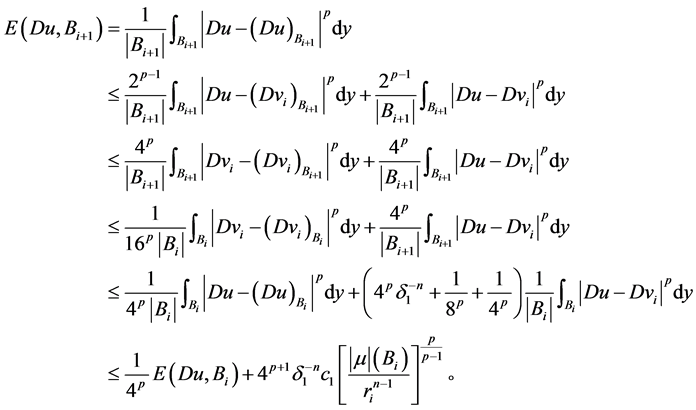
引理得证。
下面我们完成定理1.1的证明。
证明:第一步. 设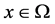 是
是 的一个Lebesgue点,
的一个Lebesgue点,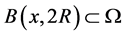 ,以下我们考虑的球都是以
,以下我们考虑的球都是以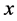 为球心的。我们选取
为球心的。我们选取
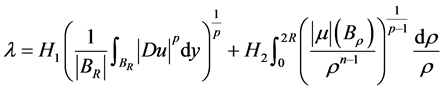 , (2.12)
, (2.12)
其中
 且
且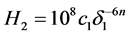 。 (2.13)
。 (2.13)
要证明定理1.1的结论,只需证明
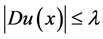 。 (2.14)
。 (2.14)
我们定义
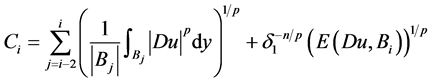 。 (2.15)
。 (2.15)
其中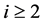 为整数。对
为整数。对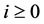 我们有
我们有
 , (2.16)
, (2.16)
由 的选取,可知对
的选取,可知对 有下式成立
有下式成立
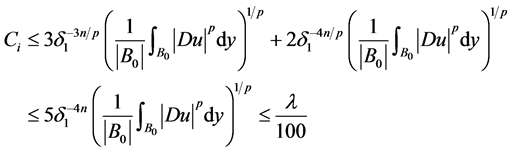 (2.17)
(2.17)
又因为
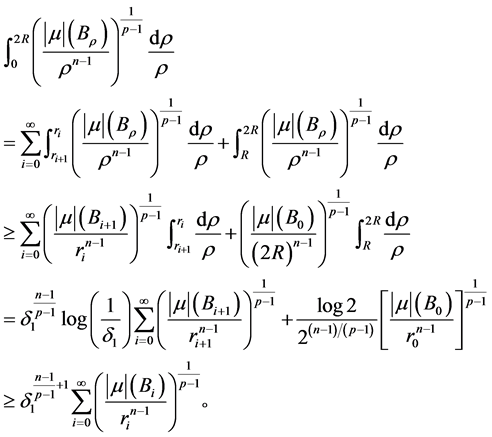 (2.18)
(2.18)
所以,由(2.12)式和(2.13)式的 ,可知
,可知
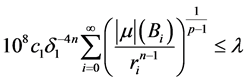 , (2.19)
, (2.19)
且
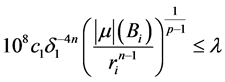 。 (2.20)
。 (2.20)
第二步. 由(2.17)式,不失一般性,我们可假设存在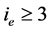 ,使得
,使得
 且
且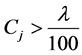 ,
,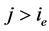 。 (2.21)
。 (2.21)
否则,对递增序列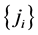 (任意
(任意 ),都有
),都有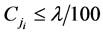 。由于
。由于 是
是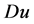 的一个Lebesgue点,则有
的一个Lebesgue点,则有
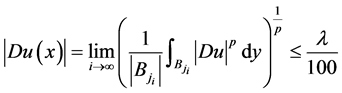 。
。
故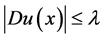 ,结论得证。
,结论得证。
第三步. 下面我们在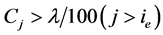 情况下继续定理1.1的证明。简记
情况下继续定理1.1的证明。简记
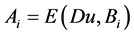 且
且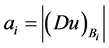 。
。
由(2.15)式和(2.21)式,可知
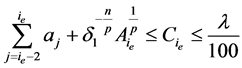 。 (2.22)
。 (2.22)
现在,我们用归纳法证明:当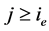 时,有下式成立
时,有下式成立
 。 (2.23)
。 (2.23)
即假设当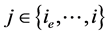 时,(2.23)式成立,证明
时,(2.23)式成立,证明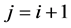 时,(2.23)式仍成立。首先,由引理2.3可知
时,(2.23)式仍成立。首先,由引理2.3可知
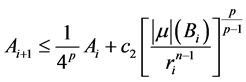 ,
,
即
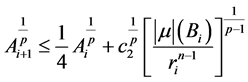 。 (2.24)
。 (2.24)
结合(2.20)式和(2.23)式,有
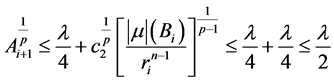 。 (2.25)
。 (2.25)
进一步,由(2.24)式对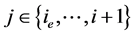 求和,可得
求和,可得
 ,
,
因此
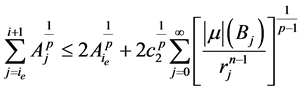 。 (2.26)
。 (2.26)
另一方面,又因为
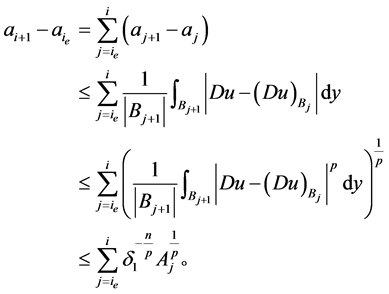
结合(2.19)式,(2.22)式和(2.26)式,可得
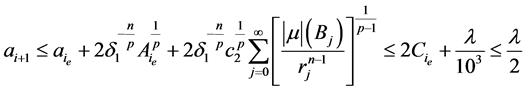 。
。
所以,由(2.25)式和上式,即有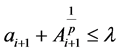 成立。综上所述,对任意
成立。综上所述,对任意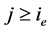 ,(2.23)式成立。最后,由于
,(2.23)式成立。最后,由于 是
是 的Lebesgue点,故
的Lebesgue点,故
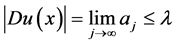 。
。
从而我们完成了定理1.1的证明。
文章引用
王墨琴. 拟线性p-调和型椭圆方程的梯度估计
Gradient Estimates for Quasilinear Elliptic p-Laplacean Equations[J]. 理论数学, 2016, 06(05): 441-448. http://dx.doi.org/10.12677/PM.2016.65060
参考文献 (References)
- 1. Hedberg, L. and Wolff, T. (1983) Thin Sets in Nonlinear Potential Theory. Annales de l’institut. Fourier, 33, 161-187. http://dx.doi.org/10.5802/aif.944
- 2. Kilpeläinen, T. and Malý, J. (1992) Degenerate Elliptic Equations with Measure Data and Nonlinear Potentials. Annali della Scuola Normale Superiore di Pisa Classe di Scienze (IV), 19, 591-613.
- 3. Kilpeläinen, T. and Malý, J. (1994) The Wiener Test and Potential Estimates for Quasilinear Elliptic Equations. Acta Mathematica, 172, 137-161. http://dx.doi.org/10.1007/BF02392793
- 4. Trudinger, N. and Wang, X. (2002) On the Weak Continuity of Elliptic Operators and Applications to Potential Theory. American Journal of Mathematics, 124, 369-410. http://dx.doi.org/10.1353/ajm.2002.0012
- 5. Korte, R. and Kuusi, T. (2010) A Note on the Wolff Potential Estimate for Solutions to Elliptic Equations Involving Measures. Advances in Calculus of Variations, 3, 99-113. http://dx.doi.org/10.1515/acv.2010.005
- 6. Duzaar, F. and Mingione, G. (2011) Gradient Estimates via Non-Linear Potentials. American Journal of Mathematics, 133, 1093-1149. http://dx.doi.org/10.1353/ajm.2011.0023
- 7. Duzaar, F. and Mingione, G. (2010) Gradient Estimates via Linear and Nonlinear Potentials. Journal of Functional Analysis, 259, 2961-2998. http://dx.doi.org/10.1016/j.jfa.2010.08.006
- 8. Mingione, G. (2011) Gradient Potential Estimates. Journal of the European Mathematical Society, 13, 459-486. http://dx.doi.org/10.4171/jems/258
- 9. Kuusi, T. and Mingione, G. (2013) Linear Potentials in Nonlinear Potential Theory. Archive for Rational Mechanics and Analysis, 207, 215-246. http://dx.doi.org/10.1007/s00205-012-0562-z
- 10. Lieberman, M. (1991) The Natural Generalization of the Natural Conditions of Ladyzhenskaya and Urall’tseva for Elliptic Equations. Communications in Partial Differential Equations, 16, 311-361. http://dx.doi.org/10.1080/03605309108820761
- 11. Fan, X. (2007) Global C^(1,α) Regularity for Variable Exponent Elliptic Equations in Divergence Form. Journal of Differential Equations, 235, 397-417. http://dx.doi.org/10.1016/j.jde.2007.01.008
- 12. Kinnunen, J. and Zhou, S. (1999) A Local Estimate for Nonlinear Equations with Discontinuous Coefficients. Communications in Partial Differential Equations, 24, 2043-2068. http://dx.doi.org/10.1080/03605309908821494
- 13. DiBenedetto, E. and Manfredi, J. (1993) On the Higher Integrability of the Gradient of Weak Solutions of Certain Degenerate Elliptic Systems. American Journal of Mathematics, 115, 1107-1134. http://dx.doi.org/10.2307/2375066
- 14. Manfredi, J. (1984) Regularity for Minima of Functionals with p-Growth. Journal of Differential Equations, 76, 203- 212. http://dx.doi.org/10.1016/0022-0396(88)90070-8
- 15. Boccardo, L. and Gallouët, T. (1989) Nonlinear Elliptic and Parabolic Equations Involving Measure Data. Journal of Functional Analysis, 87, 149-169. http://dx.doi.org/10.1016/0022-1236(89)90005-0
- 16. Boccardo, L. and Gallouët, T. (1992) Nonlinear Elliptic Equations with Right-Hand Side Measures. Communications in Partial Differential Equations, 17, 641-655. http://dx.doi.org/10.1080/03605309208820857
- 17. Mingione, G. (2007) The Calderón-Zygmund Theory for Elliptic Problems with Measure Data. Annali della Scuola Normale Superiore di Pisa Classe di Scienze (V), 6, 195-261.