Pure Mathematics
Vol.
09
No.
04
(
2019
), Article ID:
31026
,
6
pages
10.12677/PM.2019.94071
PSL(2,2n) and Simple 3-(2n + 1,2ld + 1,λ) Designs Where l Is Odd, d|(2n − 1) and d ≥ 3
Lele Wei, Weixia Li*
School of Mathematics and Statistics, Qingdao University, Qingdao Shandong

Received: Jun. 4th, 2019; accepted: Jun. 14th, 2019; published: Jun. 27th, 2019

ABSTRACT
Let be the projective line. Let l be an odd integer. The integer d satisfies and d ≥ 3. In this paper, we determined the parameter set of simple 3-designs from PSL(2,2n) with block size 2ld + 1 where the stabilizer of the initial block contains order d element of PSL(2,2n) and calculated the number of the orbits which form the simple 3-design with that parameter set. By using the orbits of PSL(2,2n) on the X, the results show that the number of the orbits is which forms the simple design.
Keywords:Simple t-Designs, Projective Special Linear Group, Automorphism Group

PSL(2,2n)与单纯3-(2n + 1,2ld + 1,λ)设计(l为奇数,d|(2n − 1)且d ≥ 3)
魏乐乐,李伟霞*
青岛大学数学与统计学院,山东 青岛

收稿日期:2019年6月4日;录用日期:2019年6月14日;发布日期:2019年6月27日

摘 要
令 是射影直线。设l为奇数,d为满足 且d ≥ 3的正整数。本文确定了以PSL(2,2n)为自同构群,区组长度为2ld + 1,初始区组的稳定子群中含有d阶元的单纯3-设计的参数,并计算了构成这一参数的轨道的条数。利用PSL(2,2n)在X上作用的轨道,得到如下结论:这类单纯3-设计的参数为 ,构成这一设计的轨道的条数为 。
关键词 :单纯t-设计,射影特殊线性群,自同构群

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1.1. 研究背景
参数为 的一个设计,简称t-设计,定义为符合以下条件的一对符号 :
1) X是一个v-集合;
2) 是X的一组k-子集;
3) X的任意给定的t-子集都恰好含于 的 个成员之中。
X的元素称为点, 的成员称为区组。若一个 设计不包含重复的区组,则称这个设计为单纯的。在本文中我们只考虑单纯t-设计。
令
,则对于任意的
,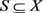 ,
。
称为S的轨道,
称为S的稳定子群,且
。
的一个自同构是指具有下述性质的X的置换g:如果
,则
。G是
的自同构群当且仅当区组集
是G作用下X的k-子集的轨道的并。
,
。
称为S的轨道,
称为S的稳定子群,且
。
的一个自同构是指具有下述性质的X的置换g:如果
,则
。G是
的自同构群当且仅当区组集
是G作用下X的k-子集的轨道的并。
令q为素数幂,
为射影直线。对任意的
,定义
, ,
,
。所有行列式为非零平方元的线性分式的集合构成线性分式群
,它同构于
。即
,
,
。所有行列式为非零平方元的线性分式的集合构成线性分式群
,它同构于
。即
.
设
,其中p为素数。利用
为设计的自同构群来研究t-设计是一个可行的方法。特别的,文献 [1] 已完整解决了以
为自同构群,区组长度为k的3-设计的存在性问题,其中
。文献 [2] [3] [4] [5] 完整讨论了以
为自同构群,区组长度为k (
)的单纯3-设计的存在性问题。文献 [6] [7] 介绍了以
为自同构群,区组长度为d和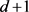 的单纯3-设计的有关结果,这里
。文献 [8] - [13] 找到了一些
时的t-设计存在的例子。
的单纯3-设计的有关结果,这里
。文献 [8] - [13] 找到了一些
时的t-设计存在的例子。
注意到当 时,对于任意的区组长度k总满足 。又 在X上的作用是精确3重传递的,故任意不相交的k-子集的轨道的并可构成单纯 设计,其中 为正整数。
本文只考虑
的情形。用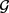 表示
,用
表示
,用
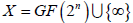 表示射影直线。总假设l为奇数,d为满足
且
的整数。利用
在X上作用的轨道,确定了以
为自同构群,区组长度为
,初始区组的稳定子群中含有d阶元的单纯3-设计的参数,并计算了满足这一参数的轨道的条数。得到了如下结果:
表示射影直线。总假设l为奇数,d为满足
且
的整数。利用
在X上作用的轨道,确定了以
为自同构群,区组长度为
,初始区组的稳定子群中含有d阶元的单纯3-设计的参数,并计算了满足这一参数的轨道的条数。得到了如下结果:
定理:令B为 中一个d阶元的2l个d圈及其一个不动点所构成的X的 -子集,则 构成一个 设计。构成这一设计的轨道的条数为 。
1.2. 预备知识
引理1 [14] :设 ,g的阶为h且 ,则g有a个不动点和 个h圈。其中当 时, ;当 时, ;当 时, 。
注:由引理1易知若B为X的一个k-子集, 当且仅当B由g的q个h圈和r个不动点构成,其中 , 。
引理2 [14] : 的一个非平凡子群必为下列之一:
1)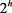 阶初等Abel群,其中
;
阶初等Abel群,其中
;
2) d阶循环群,其中 ;
3) 二面体群 ,其中 ;
4) 阶的初等Abel群和d阶循环群的半直积,其中 ;
5) ,其中 ;
6) 交错群 。
引理3 [6] :类型(4)的子群不可能是2d阶的。
引理4 [14] :所有二面体群 在 中共轭。
以下总假设 且 , 为 中的一个d阶元, , , ,m为任意正整数,l为任意奇数。
引理5 [6] : 为一个二面体群 。
引理6 [7] :若S为一个 -子集,则无二面体群 包含在 中。
由引理6易得下面的推论。
推论1:若S为一个 -子集,则无二面体群 包含在 中。
证明:若存在一个二面体群 ,由引理4及引理5知存在 ,使得 。由引理1知 由 的m个d圈和1个不动点构成,则 中恰包含0和 中的一个元素。又因为 ,由此推得若 必有 ,产生矛盾。证毕。
引理7 [6] :若S为X的k-子集,则 是一个单纯 设计,其中 。
2 定理的证明
引理8:令B为 中一个d阶元的2l个d圈及其一个不动点所构成的X的 -子集,则 构成一个 设计。
证明:由于 中有d阶元,由引理2知 不为类型(1)。由推论1知 不为类型(3)。进一步的 不为类型(5),否则存在一个二面体群 包含在 中,与推论1矛盾。又类型(6)是类型(4)的一种情形,综上述 只能为类型(2)或类型(4)的子群。可设 ,其中h为非负整数。由引理7知 为整数,又l是奇数,故 或1。再由引理3知 。故 构成一个 设计。
推论2:令S为X的 -子集,若 中有d阶元,则 为d阶循环群。
引理9:设S是X的 -子集,若 中有d阶元,则轨道 中包含形如 的区组。其中 为 中的一个d阶元, ( )。
引理10:若 是一个 设计,则轨道 中包含m个形如 的区组。其中 为 中的一个d阶元, ( )。
证明:设S为轨道 中的一个区组。由引理7得 ,即d阶循环群。由引理9可设
.
若
与S位于同一条轨道,则存在 中的一个线性分式 ,使得 。设 , 。由于 且 ,从而 。又 ,由此可得 。即 。对于 ,若 ,则对任意的 ,有 。即
.
由上述等式知存在 ,使得
.
故只能 , 且 。即 。可令 ,其中 。因此
.
又 ,令 ,从而 或 ,其中 。下分两种情况讨论:
1) 若 ,从而 。
2) 若 ,不失一般性,可令 ,从而
.
故对于 1 ≤ k ≤ m−1,必存在 。即
.
令 Math_207#,其中 ,则上述 。综上述若 当且仅当 Math_212#。
下证 互不相同。由此说明 中包含m个形如 的区组。对于任意的 ,若 ,则 ,即 。从而 ,即
.
这是不可能的。
引理11:构成 设计的轨道的条数为 。
证明:设l为奇数,
为
中的一个d阶元,
(
)。令
,易得
中元素的个数为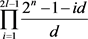 。再由引理10可得构成
设计的轨道条数为
。
。再由引理10可得构成
设计的轨道条数为
。
定理:令B为 中一个d阶元的2l个d圈及其一个不动点所构成的X的 -子集,则 构成一个 设计。构成这一设计的轨道的条数为 。
证明:利用引理8和引理11可以得到定理。
推论3:令B为 中一个d阶元的2l个d圈及其一个不动点所构成的X的 -子集,则对于任意的正整数t,其中 ,可构造出单纯 设计。
致谢
衷心感谢导师李伟霞在本文写作过程中的悉心指导!
文章引用
魏乐乐,李伟霞. PSL(2,2n)与单纯3-(2n + 1,2ld + 1,λ)设计(l为奇数,d|(2n - 1)且d ≥ 3)
PSL(2,2n) and Simple 3-(2n + 1,2ld + 1,λ) Designs Where l Is Odd, d|(2n - 1) and d ≥ 3[J]. 理论数学, 2019, 09(04): 540-545. https://doi.org/10.12677/PM.2019.94071
参考文献
- 1. Cameron, P.J., Maimani, H.R., Omidi, G.R. and Tayfeh-Rezaie, B. (2006) 3-Designs from . Discrete Mathematics, 306, 3063-3073.
https://doi.org/10.1016/j.disc.2005.06.041 - 2. Keranen, M.S. and Kreher, D.L. (2004) 3-Designs of with Block Sizes 4 and 5. Journal of Combinarorial Designs, 12, 103-111.
https://doi.org/10.1002/jcd.10068 - 3. Li, W. and Shen, H. (2008) Simple 3-Designs of with Block Size 6. Discrete Mathematics, 308, 3061-3072.
https://doi.org/10.1016/j.disc.2007.08.030 - 4. Li, W. and Shen, H. (2010) Simple 3-Designs of with Block Size 7. Journal of Combinarorial Designs, 16, 1-17.
https://doi.org/10.1002/jcd.20141 - 5. Gong, L.Z. and Fan, G.B. (2018) Simple 3-Designs of with Block Size 8. Utilitas Mathematica, 106, 3-9.
- 6. 李伟霞. 区组长度为 因子的单纯3-设计[J]. 上海交通大学学报, 2007, 41(5): 845-847.
- 7. Li, W. and Shen, H. (2011) Simple 3-Designs with Block Sizes from Where . Journal of Combinarorial Designs, 51, 235-241.
- 8. Bierbrauer, J. (1993) A Family of 4-Designs with Block Size 9. Discrete Mathematics, 138, 113-117.
https://doi.org/10.1016/0012-365X(94)00192-L - 9. 刘伟俊, 谭琼华, 龚罗中. 旗传递 设计[J]. 江苏大学学报, 2010, 31(5): 612-615.
- 10. 刘伟俊, 姚蹈, 陈静. 一般射影线性群 与 设计[J]. 数学理论与应用, 2010, 30(1): 123-128.
- 11. 陈静, 陈暑波, 刘伟俊. 二维射影线性群与区传递 设计[J]. 中国科学, 2010, 40(11): 1045-1054.
- 12. 唐剑雄, 陈静, 刘伟俊, 等. 二维射影线性群与区传递 设计[J]. 数学进展, 2012, 41(5): 547-553.
- 13. 杨冠, 刘伟俊. 射影线性群区传递作用于 设计[J]. 浙江大学学报, 2013, 40(5): 489-491.
- 14. Dickson, L.E. (1958) Linear Groups with an Introduction to the Galois Field Theory. Dover Publications, New York, 260-287.
NOTES
*通讯作者。