Pure Mathematics
Vol.
09
No.
05
(
2019
), Article ID:
31403
,
10
pages
10.12677/PM.2019.95081
Discussion on a Class of Number Theory Equations Containing Generalized Euler’s Totient Function
Lu Cai, Changxin Lai, Yanhua Yang
College of Mathematics and Computer Science, Aba Teachers University, Wenchuan Sichuan
Email: 1538249856@qq.com
Received: Jul. 10th, 2019; accepted: Jul. 18th, 2019; published: Jul. 25th, 2019

ABSTRACT
Let
be generalized Euler function, where n and e are positive integers. Using elementary methods, the solvability of equations
,
, and
related to generalized Euler’s totient function is studied and discussed. Based on the properties of generalized Euler’s totient function and Euler’s totient function, the partial solution of the equation is obtained by the discussion of classification and segmentation.
Keywords:Generalized Euler Function, Euler Function, Equation, Positive Integer Solution
对一类包含广义欧拉函数的数论方程的讨论
蔡 璐,赖常鑫,杨燕华
阿坝师范学院数学与计算机科学学院,四川 汶川
Email: 1538249856@qq.com
收稿日期:2019年7月10日;录用日期:2019年7月18日;发布日期:2019年7月25日

摘 要
令
为广义欧拉函数,其中n与e都是正整数。利用初等方法,研究讨论了与广义欧拉函数有关的数论方程
, 以及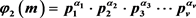 的可解性。基于广义欧拉函数的性质,利用初等数论的一些结论以及分类、分段的讨论方式,获得以上方程的正整数解的相关结论。
的可解性。基于广义欧拉函数的性质,利用初等数论的一些结论以及分类、分段的讨论方式,获得以上方程的正整数解的相关结论。
关键词 :广义欧拉函数,欧拉函数,方程,正整数解

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言与主要结论
Euler函数φ(n)是数论中非常重要而有意义的一类函数,定义为
中与n互素的个数。为了将Lehmer同余式从模素数的平方推广到模任意整数的平方,蔡天新 [1] 等对广义Euler函数的作出了如下定义。
定义:广义欧拉函数φe(n)
(1.1)
即序列
中与n互素的数的个数。显然,当e = 1时,广义欧拉函数φe(n)就是欧拉函数φ(n)。
当e = 2时,由广义欧拉函数定义,容易验证,
,,对
,有
(1.2)
关于Euler函数φ(n)以及广义Euler函数φe(n)的性质以及与广义Euler函数相关的数论方程的研究非常活跃。文献 [2] [3] 对广义Euler函数的性质有一定的研究。同时,对于包含广义Euler函数的方程也有所讨论,如文献 [4] - [14] 对包含广义Euler函数φe(n)以及ω(n)和Ω(n)的方程的可解性;文献 [15] [16] [17] [18]
讨论了形如
方程的可解性;文献 [19] [20] 对包含Euler函数和广义Euler函数的方程的正整数解进行了研究;文献 [21] - [28] 给出了形如
, 这种形式的方程的可解性。
本文将研究更一般的方程,即方程
(1.3)
(1.4)
以及
(1.5)
的可解性,其中
是给定的素数。求出了一些方程的全部解,并获得了一些一般性的结论。本文的主要结论是:
定理1:方程(1.3)的所有非负整数解(m, x, y) (表1所示)为

Table 1. All nonnegative integer solutions of Equation (1.3) (m, x, y)
表1. 方程(1.3)的所有非负整数解(m, x, y)
定理2:方程(1.4)的所有非负整数解(m, x, y) (表2和表3所示)为
1) 若
时,
,有

Table 2. In the case of p = 2, q > 5, the nonnegative integer solutions of Equation (1.4) (m, x, y)
表2. 在p = 2,q > 5的情况下,方程(1.4)的非负整数解(m, x, y)
2) 若
,,即
,有

Table 3. In the case of p, q ≥ 5, the nonnegative integer solutions of Equation (1.4) (m, x, y)
表3. 在p,q ≥ 5的情况下,方程(1.4)的非负整数解(m, x, y)
定理3:方程(1.5)的解(m, x, y)满足
1)
,当
(
)时,
,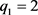 ,
(
),且
(
)。
,
(
),且
(
)。
2)
,必有
,,,其中
,则
,且
, 。
2. 方程φ2(m) = 2x3y的解
本节讨论方程(1.3)的解,由于
,
故令
其中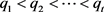 且均为质数,则
且均为质数,则
(2.1)
2.1. 情况1:t = 1
当
时,有
(2.2)
情况1.1:当
时,可得
, (
),故
, 。
情况1.2:当
时, 。
。
情况1.2.1:当
时,
,可得
(
),
(
),故
, 。
情况1.2.2:当
时,
,可得
(
),
(
),故
, 。
2.2. 情况2:t = 2
当
时,有
(2.3)
情况2.1:当
时,有
,可得
,, (
;
)。故
, 。
情况2.2:当
, 时,有
。
情况2.2.1:当
, (
,且为质数)时,
,可得
(
),
(
),
(
),故
, 。
情况2.2.2:当
, (
,且为质数)时,
,可得
(
),
(
),
(
),故
, 。
情况2.3:当 ,
时,有
。
,
时,有
。
当
, 时,
,可得
(
),
(
),
(
)。故
, 。
2.3. 情况3:当t ≥ 3时,有
(2.4)
情况3.1:当
(
)时,有
可得,
, (
),故
, 。
情况3.2:当
, (
)时,有
。
情况3.2.1:当
, (
且为质数,
)时
,则可得
, (
),故
, 。
情况3.2.2:当
, (
且为质数,
)时,
,可得
, (
),故
,,, 。
情况3.3:当
,, (
)时,有
。
情况3.3.1:当
,, (
且为质数,
)时,
,可得
, (
),故
,,当
时,
。
于是定理1得证。
3. 方程
的解
本节将在定理1:
的解的情况的基础上,对更一般的情况来作进一步的讨论,即
(其中p,q为质数,且)。当
, 时,与定理1相同,下面,我们讨论
,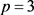 不同时成立的情况。
不同时成立的情况。
3.1. 情况A
,,,则
(3.1)
同样地,我们设
其中
且均为质数。
情况1:t = 1当
时,
。
情况1.1:当
时,
, (
),故
, (当
时,
;
时,
)。
情况1.2:当 时,
。
时,
。
情况1.2.1:当
时,
,可得
(
),
(
),故
, 。
情况1.2.2:当
时,
,可得
(
),
(
),故
, 。
情况2:t = 2当
时,
。
情况2.1:当
时,有
,可得
,, (
;
),故
, 。
情况2.2:当
, 时,有
。
情况2.2.1:当
(
,且为质数)时,
,可得
(
),
(
),
(
),故
, 。
情况2.2.2:当
时,(
,且为质数)
,可得
(
),
(
),
( ),故
, 。
),故
, 。
情况2.3:当
, 时,有
,此时必定有
,则有
(
),
(
),
(
),故
, 。
情况2.4:当
, 时,有
。
当
, 时,
,可得
(
),
(
),
(
),故
, 。
情况3:t = 3当t = 3时,
。
情况3.1:当
时,有
,可得
, (
),
, (
)
当 时,必有
且
,故
, 。
时,必有
且
,故
, 。
情况3.2:当
, 时,有
。
情况3.2.1:当
时,
,可得
(
)。
(
),
, (
),
当
时,必有
且
,故
, 。
情况3.2.2:当
时,(
,且为质数)
,可得
(
),
(
)当
时,必有
,, (
),
且
,故
, 。
情况3.3:当
,, 时,有
,可得
(
),
(
),
(
),
(
)且 ,故
, 。
,故
, 。
情况3.4:当
, 时,有
。
则
,可得
(
),
(
),
(
),
(
)且
,故
, 。
情况3.5:当
,, 时,有
。
则
, (
,且为质数)时,
,可得,
(
),
(
),
(
)当
时,必有
, (
)当
时,必有
且
,故
, 。
情况4:
时,
。
情况4.1:当
(
)时,有
可得
, (
),故
, 。
情况4.2:当
, (
)时,有
。
情况4.2.1:当
, (
且为质数,
)时,
,可得
, (
),故
, 。
情况4.2.2:当
(
且为质数,
)时,
,可得
, (
),当
时,
,故
, 。
情况4.3:当
, (
)时,有
。
当
(
且为质数,
)时,
,可得
, (
),当
时,
,故
, 。
情况4.4:当
,, (
)时,有
。
情况4.4.1:当
,, (
且为质数,
)时,
,可得
, (
),故
, 。其中
, 不能同时取。
3.2. 情况B
由于当
时,必有
,与定理1相同,故下面讨论
, 时的情况
当
, 时,
,,则
(3.2)
情况1:t = 1:当
时,
情况1.1:当
时,
, (
),故
, (当
时,
;
时,
)。
情况1.2:当
时,
。通过分析易知
,则
或者
。
情况1.2.1:当
时,
,可得
, (
),此时只有在
下有解。
(
),故
, 。
情况1.2.2:当
时,
,可得
(
),
(
),故
, 。
情况2:t = 2当
时,
。
情况2.1:当
时,有
,由于
,易知
, 方程不成立,无解。
情况2.2:当
, 时,有
,无解。
情况2.3:当
, 时,有
,无解。
情况2.4:当
, 时,有
,无解。
情况3:t ≥ 3当
时,
,无解。
于是定理2得证。
4. 方程
的解
本节将在前面两个定理的基础上,延申到更加一般的情况:即
(令
且均为质数),由分析知,必有
。则
(
)。由
,其中
且均为质数,则可得,
(4.1)
其中必有
,因为当
时,方程(4.1)无解。
4.1. 情况1
当
时,
(令
)
情况1.1.1:当
时,由
,可得
, (其中
),
,,, 。
情况1.1.2:当
时,由
,易知
,,可得
,, (其中
,且不包含
这一素数),
,,
(
)
之后也为0。
4.2. 情况2
当
时,
(令
)
情况2.1.1:当
时,由
,可得
,,,,, 。
情况2.1.2:当
, 时,有
,当
时,
,可得
(
),
,,,,其中
, (
)
之后也为0。
情况2.1.3:当
, 时,由
,易知
,可得
,,,,,, (
)
之后也为0,
(
)
之后也为0。
4.3. 情况3
当
时,
。
情况3.1.1:当
时,由
,可得
,,,, 。
情况2.1.2:当
, 时,有
,当
时,
,可得
(
),
,,,, (
),
之后也为0。
情况2.1.3:当
,, 时,由
,易知
,,可得
(
),
,,,, (
)
之后也为0。
(
)
之后也为0。
情况2.1.4:当
,,, 时,由
,易知
,可得
(
),
,,,, (
),
之后也为0。
(
),
之后也为0。
(
)
之后也为0。
由此可得,当
时,
。
将以上讨论概括为以下两个情况:
情况1:
,当
(
)时,
,, (
),且
(
)。
情况2:
,必有
,,,其中
,则
,且
, 。
于是定理3得证。
致谢
作者衷心感谢阿坝师范学院杨仕椿教授的悉心指导与无私教诲!
基金项目
全国大学生创新训练项目(201810646012),阿坝师范学院教学科研项目(201805087, 20170203, 20171510, 20171515)。
文章引用
蔡 璐,赖常鑫,杨燕华. 对一类包含广义欧拉函数的数论方程的讨论
Discussion on a Class of Number Theory Equations Containing Generalized Euler’s Totient Function[J]. 理论数学, 2019, 09(05): 611-620. https://doi.org/10.12677/PM.2019.95081
参考文献
- 1. Cai, T.X., Fu, X.D. and Zhou, X. (2007) A Congruence Involving the Quotients of Euler and Its Applications (II). Acta Arithmetica, 130, 203-214.
https://doi.org/10.4064/aa130-3-1
- 2. Cai, T.X., Shen, Z.Y. and Hu, M.J. (2013) On the Parity of the General-ized Euler Function. Advances in Mathematics, 42, 505-510.
- 3. Shen, Z.Y., Cai, T.X. and Hu, M.J. (2016) On the Parity of the Generalized Euler Function (II). Advances in Mathematics, 45, 509-519.
- 4. 俞洪玲, 沈忠燕. 与广义欧拉函数有关的方程[J]. 浙江外国语学院学报, 2012(3): 91-97.
- 5. 金明艳, 沈忠燕. 方程φ2(n) = 2Ω(n)和φ2(φ2(n)) = 2Ω(n)的可解性[J]. 浙江外国语学院学报, 2013(4): 47-52.
- 6. 张四保, 陈佳宏, 杨燕妮. 一个包含广义Euler函数φ3(n)方程的解[J]. 科技通报, 2019, 35(3): 7-10.
- 7. 张四保. 与广义Euler函数有关的一方程的解[J]. 科技通报, 2018, 34(8): 1-5+9.
- 8. 张四保. 广义Euler函数方程φ6(n) = 2ω(n)的解[J]. 西南师范大学学报(自然科学版), 2018, 43(2): 36-41.
- 9. 张四保. 数论函数方程φ(φ(n)) = 2ω(n)3ω(n)的奇数解[J]. 西南师范大学学报(自然科学版), 2017, 42(2): 1-4.
- 10. 张四保. 包含Euler函数φ(n)与函数Ω(n)方程的解[J]. 山西大学学报(自然科学版), 2017, 40(2): 225-228.
- 11. 多布杰. 关于数论函数方程φ(φ(n)) = 2ω(n)的可解性问题研究[J]. 西藏大学学报(自然科学版), 2012, 27(1): 102-106.
- 12. 张四保. 与三个数论函数有关的两个方程的解[J]. 数学的实践与认识, 2018, 48(10): 296-300.
- 13. 陈斌, 吉宇锋. 关于一类包含Euler函数方程的解[J]. 河南科学, 2009, 27(12): 1500-1501.
- 14. 陈国慧. 一个包含Euler函数的方程[J]. 纯粹数学与应用数学, 2007(4): 439-445+457.
- 15. 王蓉, 廖群英. 方程 的可解性[J]. 纯粹数学与应用数学, 2016, 32(5): 481-494.
- 16. 王容. 一类广义欧拉函数及相关方程[D]: [硕士学位论文]. 成都: 四川师范大学, 2018.
- 17. 王容, 廖群英. 关于广义欧拉函数φ5(n)[J]. 四川师范大学学报(自然科学版), 2018, 41(4): 445-449.
- 18. 王容, 罗文力, 廖群英. 方程φ3(n) = d/n的可解性[J]. 成都信息工程大学学报, 2017, 32(1): 95-101.
- 19. 张四保. Euler函数φ(n)与广义Euler函数φ2(n)混合的两个方程[J]. 北华大学学报(自然科学版), 2019, 20(1): 8-14.
- 20. 张四保, 官春梅, 杨燕妮. 广义Euler函数φ2(n)与Euler函数φ(n)混合的一方程[J]. 数学的实践与认识, 2018, 48(9): 265-268.
- 21. 张四保. 数论函数方程φ(xy) = kφ(x)φ(y)的正整数解[J]. 黑龙江大学自然科学学报, 2017, 34(2): 181-185.
- 22. 杨张媛, 赵西卿, 白继文. 一个包含Euler函数的方程[J]. 贵州师范大学学报(自然科学版), 2018, 36(4): 80-88.
- 23. 白继文, 赵西卿. 与Euler函数有关的一个方程的正整数解[J]. 延安大学学报(自然科学版), 2017, 36(2): 5-7.
- 24. 郭瑞, 赵西卿. 一类包含Euler函数方程的正整数解[J]. 江汉大学学报(自然科学版), 2016, 44(5): 411-421.
- 25. 鲁伟阳, 高丽, 王曦浛. 有关Euler函数φ(n)的方程的可解性问题[J]. 江西科学, 2016, 34(1): 15-16+23.
- 26. 张四保, 杜先存. 一个包含Euler函数方程的正整数解[J]. 华中师范大学学报(自然科学版), 2015, 49(4): 497-501.
- 27. 高丽, 张佳凡. Euler函数方程φ(xy) = 11(φ(x)+φ(y))的正整数解[J]. 云南师范大学学报(自然科学版), 2017, 37(5): 13-19.
- 28. 王曦浛, 高丽, 鲁伟阳. 一个包含Euler函数方程的正整数解[J]. 贵州大学学报(自然科学版), 2016, 33(4): 25-29.


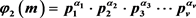 的可解性。基于广义欧拉函数的性质,利用初等数论的一些结论以及分类、分段的讨论方式,获得以上方程的正整数解的相关结论。
的可解性。基于广义欧拉函数的性质,利用初等数论的一些结论以及分类、分段的讨论方式,获得以上方程的正整数解的相关结论。


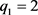 ,
(
),且
(
)。
,
(
),且
(
)。 且均为质数,则
且均为质数,则 。
。 ,
时,有
。
,
时,有
。 不同时成立的情况。
不同时成立的情况。 时,
。
时,
。 ),故
, 。
),故
, 。 时,必有
且
,故
, 。
时,必有
且
,故
, 。 ,故
, 。
,故
, 。