Pure Mathematics
Vol.
10
No.
02
(
2020
), Article ID:
34231
,
4
pages
10.12677/PM.2020.102015
Periodicity of Entire Functions Concerning Difference
Bingmao Deng1, Shiwen Yang2
1School of Financial Mathematics and Statics, Guangdong University of Finance, Guangzhou Guangdong
2Institute of Mathematics, South China Agricultural University, Guangzhou Guangdong

Received: Jan. 24th, 2020; accepted: Feb. 12th, 2020; published: Feb. 19th, 2020

ABSTRACT
This paper studied the periodicity of entire functions with its difference, and proved: Let be a transcendental entire function of finite order, and d be a Picard exceptional value of . If is a periodic function, then is also a periodic function.
Keywords:Entire Function, Picard Exceptional Value, Periodic Function

与差分相关的整函数周期性问题
邓炳茂1,杨世伟2
1广东金融学院,金融数学与统计学院,广东 广州
2华南农业大学,应用数学研究所,广东 广州

收稿日期:2020年1月24日;录用日期:2020年2月12日;发布日期:2020年2月19日

摘 要
本文主要研究了有穷级整函数与差分相关的周期性问题,主要证明了:如果 是有穷级超越整函数,d是
的一个Picard例外值,如果
是有穷级超越整函数,d是
的一个Picard例外值,如果
 是周期函数,则
也是周期函数。
是周期函数,则
也是周期函数。
关键词 :整函数,Picard例外值,周期函数

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言及主要结果
假设读者熟悉亚纯函数Nevanlinna值分布理论的基本内容及相关标准符号(见参考文献 [1] [2] [3])。特别的, 表示整函数f的级,当 时,称f为有穷级整函数。
设 是复平面上的整函数,定义其差分算子为
是复平面上的整函数,定义其差分算子为
,.
2018年,王琼、扈培础 [4] 研究了杨重俊提出的如下猜想:
猜想1:如果
是超越整函数,对某个正整数k,如果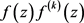 是周期函数,则
也是周期函数。
是周期函数,则
也是周期函数。
王琼、扈培础 [4] 证明了以下特殊情形,猜想1是正确的,他们证明了:
定理1:如果 是超越整函数,对某个正整数k,如果
是周期函数,则
是超越整函数,对某个正整数k,如果
是周期函数,则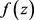 也是周期
也是周期
函数。
注1:显然 ,即定理1说明猜想1当 时是正确的。
2019年,刘凯等人 [5] 研究了在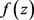 有非零Picard例外值的情形,猜想1是正确的。
有非零Picard例外值的情形,猜想1是正确的。
定理2:如果 是超越整函数, 是 的一个Picard例外值,对某个正整数k,如果 是周期函数,则 也是周期函数。
对于定理2,要求 ,自然会问,当 时,定理2结论是否成立?本文研究了该问题,证明了以下结论。
定理3:如果
是有穷级超越整函数,0是
的一个Picard例外值,对某个正整数k,如果 是以c为周期的函数,则
是以c为周期的函数,则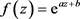 ,其中
是两个常数,并且
,即
是以
,其中
是两个常数,并且
,即
是以
2c周期的周期函数。
另外,我们将定理2中的导数替换成差分,证明了如下结论。
定理4:如果 是有穷级超越整函数,d是
是有穷级超越整函数,d是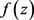 的一个Picard例外值,如果
是周期函数,则
也是周期函数。
的一个Picard例外值,如果
是周期函数,则
也是周期函数。
2. 一些引理
引理2.1 ( [6])设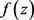 是一个有穷级亚纯函数,c是非零常数,则有
是一个有穷级亚纯函数,c是非零常数,则有
 .
.
引理2.2 ( [2])设
除
之外是非常值亚纯函数,并且满足 ,和存在一个常数
,对任意的,
时,均有
,和存在一个常数
,对任意的,
时,均有
,  ,
,
,
,
其中 是测度有穷的集合。
则 。
3. 定理3的证明
由0是
的Picard例外值,且
是有穷级超越整函数,因此存在非常数多项式
,使得
,显然
。经简单计算,可得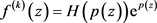 ,其中
,其中 是关于
是关于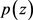 的微分多项式。显然
,否则
,得
是一个次数不超过
的多项式,这与
是超越整函数矛盾。引理2.1可得
,
的微分多项式。显然
,否则
,得
是一个次数不超过
的多项式,这与
是超越整函数矛盾。引理2.1可得
, 。
。
另外,因为 是周期函数,不妨设其周期为c,则有
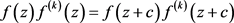 .(1)
.(1)
将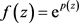 ,
,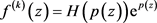 代入(1)式,可得
代入(1)式,可得
.
从而有
.
当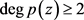 时,
.
时,
.
,
矛盾。
所以
,令
,其中
. 则
,,代入(1)式,可得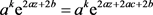 ,所以
,即得
,所以
,即得 。
。
定理3证明完毕。
4. 定理4的证明
由d是
 的Picard例外值,且
的Picard例外值,且 是有穷级超越整函数,因此存在非常数多项式
,使得
,显然
。经简单计算,可得
,若
,则显然
是以c为周期的周期函数,以下考虑
的情形。
是有穷级超越整函数,因此存在非常数多项式
,使得
,显然
。经简单计算,可得
,若
,则显然
是以c为周期的周期函数,以下考虑
的情形。
另一方面,因为 是周期函数,不访设其周期为 ,则有
.(2)
将 , 代入(2)式,
当 时,有
. (3)
可断言:
, (4)
 . (5)
. (5)
若不然,由(3)式及引理2.1,引理2.2,可得
.
矛盾。
令 ,,。
情形1。
。则
,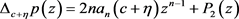 。其中
。其中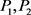 是次数不超过
是次数不超过 的多项式。可知
均是次数为
的多项式。由(5)式及引理2.2,可得
,或者
,或者
,矛盾。
的多项式。可知
均是次数为
的多项式。由(5)式及引理2.2,可得
,或者
,或者
,矛盾。
情形2。
。则
, ,
,代入(5)式,可得
,
,代入(5)式,可得
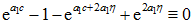 ,即
解方程,有
,或
。即
是以c或
为周期的周期函数。进一步的,若
,结合(4)式,可得
,即
解方程,有
,或
。即
是以c或
为周期的周期函数。进一步的,若
,结合(4)式,可得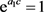 ,或
,即
是以c或
为周期的周期函数。
,或
,即
是以c或
为周期的周期函数。
当 时,有
. (6)
与上述讨论类似,可得 是以c或 为周期的周期函数。
定理4证明完毕。
基金项目
国家自然科学基金青年资助项目(11901119, 11701188);广东教育厅科研项目(2017KTECX130)。
文章引用
邓炳茂,杨世伟. 与差分相关的整函数周期性问题
Periodicity of Entire Functions Concerning Difference[J]. 理论数学, 2020, 10(02): 96-99. https://doi.org/10.12677/PM.2020.102015
参考文献
- 1. 杨乐. 值分布及其新研究[M]. 北京: 科学出版社, 1982: 5-13.
- 2. Yang, C.C. and Yi, H.X. (2003) Uniqueness Theory of Meromorphic Functions. Science Press, Beijing, 1-13.https://doi.org/10.1007/978-94-017-3626-8_1
- 3. Hayman, W.K. (1964) Mermorphic Functions. Clarendon Press, Oxford, 4-10.
- 4. 王琼, 扈培础. 关于整函数零点和周期性的研究[J]. 数学物理学报, 2018, 38(2): 209-204.
- 5. Liu, K. and Yu, P.Y. (2019) A Note on the Periodicity of Entire Functions. Bulletin of the Australian Mathematical Society, 100, 290-296. https://doi.org/10.1017/S0004972719000030
- 6. Chiang, Y.M. and Feng, S.J. (2008) On the Nevanlinna Characteristic of f(z+η) and Difference Equations in the Complex Plane. The Ramanujan Journal, 16, 105-129. https://doi.org/10.1007/s11139-007-9101-1