Pure Mathematics
Vol.
10
No.
04
(
2020
), Article ID:
35067
,
11
pages
10.12677/PM.2020.104039
The Generalized Tracial Rank of C*-Algebra
Chenchen Liu
School of Mathematical Sciences, Ocean University of China, Qingdao Shandong
Received: Mar. 21st, 2020; accepted: Apr. 9th, 2020; published: Apr. 16th, 2020

ABSTRACT
In this paper, the properties of generalized tracial rank are studied. We prove equivalence of generalized tracial rank and weak generalized tracial rank, and also prove that generalized tracial rank is closed with respect to direct sum, and unital subalgebra. Finally, the generalized tracial rank of the ideal of compact operators on a Hilbert module is given.
Keywords:Tracial Rank, Generalized Tracial Rank, Weak Generalized Tracial Rank

C*-代数的广义迹秩
刘晨晨
中国海洋大学数学科学学院,山东 青岛
收稿日期:2020年3月21日;录用日期:2020年4月9日;发布日期:2020年4月16日

摘 要
本文研究广义迹秩的性质,证明了广义迹秩与弱广义迹秩的等价性,给出了广义迹秩对直和、有单位元子代数的封闭性等性质,并研究了Hilbert模上紧算子理想的广义迹秩。
关键词 :迹秩,广义迹秩,弱广义迹秩

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
2001年林华新教授因核C*-代数分类的需要 [1] 首次提出迹秩的概念。迹秩类似于拓扑空间的维数,是非交换代数的一种拓扑秩。它是C*-代数同构的不变量,在C*-代数分类研究中起着重要的作用。
广义迹秩是起源于S. Eilers,T. A. Loring和G. K. Pedersen定义一维非交换CW复形,林华新等人在此基础上定义了广义迹秩 [2],它是迹秩概念的推广,是C*-代数分类的又一重要不变量。本文研究了广义迹秩关于直和、商、遗传子代数以及归纳极限等的性质,并证明了
。
2. 预备知识
在此先列出本文用到的记号与定义。
设A是C*-代数。
(1) 记
是A中的正元集和投射集。
(2) 记
是A的单位化。
(3) 若存在一列投射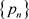 是A的近似单位,则称A是
-unital的。
是A的近似单位,则称A是
-unital的。
(4) 设
,定义函数
为
(5) 令
,若存部分等距
满足对任意的
,有
,,其中
是a的值投影,且
,则记
。
设E是C*-代数A上的Hilbert C*-模。
(1) 对任意的
,对任意的
,定义
。
(2) 令
,称
中的元素为E上的紧算子。
(3) 令D为E的子集,如果D中元素的有限A-线性组合构成的子模在E中稠密,则称D是E的生成集。如果E有有限或可数生成集,则称E是可数生成的。
(4) 记
,则
是Hilbert A-模。
3. 主要结果
定义3.1. A是unital的C*-代数,若对于任意
,,任意有限集
包含非零正元a,任意
,存在C*-子代数
以及投射
, 满足:
(1) 任给
, ;
(2) 任给
, ;
(3)
,。
则称
。
当A是non-unital的C*-代数时,若
,则称
。
注3.2. 若X是有限维紧的Hausdorff空间则
亦为有限维空间,所以
,因此
。
定理3.3. 设
是unital C*-代数,若
,则
。
证明. 任意
,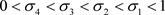 ,
以及任意有限集
,其中
,
以及任意有限集
,其中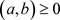 ,所以
。令
,,则由
知对上述
, 分别存在
,
,所以
。令
,,则由
知对上述
, 分别存在
,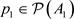 ,
, ,
满足:
,
满足:
(1) 任给
,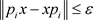 ;
;
(2) 任给
, ;
(3)
, ;
(4)
,。
令
,下证
。
因为存在有限维代数
, 及同态
, 使得
及有限维代数
, 及同态
, 使得
。
令
, 则
,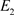 是有限维代数,
,,是
, 从
到
的同态且
,则
是有限维代数,
,,是
, 从
到
的同态且
,则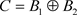 ,且
,所以
,且
,所以
(1) 任给
, ;
(2) 因为存在
,
使得
所以
所以
(任给
)。
(3)
综上得
。
□
注3.4. 设
是任意有限个C*-代数,若对于任意i,
,则
。特殊的,当A是unital C*-代数时,因为
,所以
当且仅当
。
定理3.5. 令A是unital C*-代数,若任意
,任意有限集
,存在unital C*-子代数
满足
且
,,则
。
特殊的,对
,其中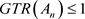 ,则
。
,则
。
证明. 任意
,,,任意有限集
,其中
。令
,则由 [3] 引理2.8知存在
, 满足引理2.8不妨设
,对于
由条件知存在unital C*-子代数
, 且
,所以对于任意i,存在
使
,存在
,使
。令
,则由
知对上述
, 以及
存在
,,, 满足:
(1) 任给
, ;
(2) 任给
,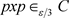 ;
;
(3)
,,
所以
(1') 任意
,
(2') 因为对于任意的i,存在
使得
,则
同理因为存在
,满足
,所以
因此任给
,。
因为
,所以
,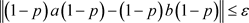 ,且因为
,
,且因为
,
所以由 [3] 引理2.8知
综上得
。
□
定义3.6. 设A是unital C*-代数,若对于任意
,,任意有限集
包含非零正元a,存在C*-子代数
以及投射
, 满足:
(1) 任给
, ;
(2) 任给
,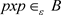 ;
;
(3)
,
则称
。
当A是non-unital的C*-代数时,若
则称
。
引理3.7. 设A为C*-代数,若
,则对任意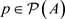 有
。
有
。
证明. 任意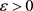 ,
,令
,
,
,令
,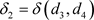 ,
,令
,
,
,令
,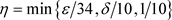 。
。
对于任意有限集
,且
,令
,对于上述
, 以及
由
知存在C*-子代数
,,, 满足:
(1) 任给
, ;
(2) 任给
, ;
(3)
,
由此得
同理 。
。
由 [4] 引理2.5.5知存在投射
, 满足
,。由(2)知存在
,,所以由 [4] 引理2.5.4知存在
,使
。则由 [4] 引理2.5.1知存在
满足
且
。
令
,则由 [3] 知
,且
满足:
(1') 任给
),
;
(2') 任给
),
;
(3')
,
所以 。
。
□
定理3.8. 设A是unital C*-代数,则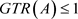 当且仅当
。
当且仅当
。
证明. 设
,则对于任意
,,,以及任意有限集
,其中
,则由
定义知当
时结论成立。下对n运用数学归纳法,假设
时结论成立,下证
时结论成立。
取
满足
,由则由 [3] 引理2.9知存在
,, 满足引理2.9,令
,则由归纳假设知存在C*-子代数
,, 满足:
(1) 任给
, ;
(2) 任给
,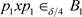 ;
;
(3)
,。
由引理3.7只对于C*-代数
,有限集
存在C*-子代数
,, 满足:
(1') 任给
, ;
(2') 任给
, ;
(3')
。
令
,,则由定理1的证明知
,且
,经过简单的计算可知
(a) 任给
, ;
(b) 任给
, ;
(c)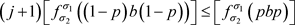 。
。
由(3')知
,又因为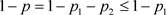 ,所以
,则由 [5] 定理3.3知
,所以
综上得
。
,所以
,则由 [5] 定理3.3知
,所以
综上得
。
□
附注3.9. 由引理3.7和定理3.8知若
,B是A的单位遗传子代数,则
。特殊的,对于A的单位理想I有
。
定理3.10. 设A是unital C*-代数,则
当且仅当任意
,。
证明. 若
,由于
,所以由注3.9知
。
若
,则任意
,,以及任意有限集
且存在
,。设
是
的标准正交基,不妨认为
,取
满足
,设
以及任意取定
,令
,则存在C*-代数
,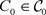 ,
,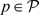 ,
,满足:
,
,满足:
(1) 任给
, ;
(2) 任给
, ;
(3)
。
由(3)知
。
令
,,则
,且
(1') 任给
, ;
(2') 任给
, ;
(3')
,。
令
,则由(3')知存在部分等距元
,满足
,,又因为我们将
看做
,所以
是A的单位遗传子代数。令
,则由引理3.7知存在C*-子代数
, 以及投射
且
满足:
(1') 任给
, ;
(2') 任给
, ;
(3')
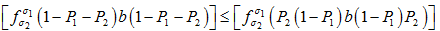 。
。
令
,易证
,,当
足够小时,对上述
,有
(a) 任给
, ;
(b) 任给
, ;
(c)
。
综上可得
。
□
推论3.11. 设A是unital C*代数,
,则对于任意的AF-代数B,有
。
证明. 由定理3.10知对于任意n有
,又因为存在正整数列
使
是
的归纳极限,所以由定理3.5知
。
□
引理3.12. 设A是unital的C*-代数,D是在A中稠密的自伴子代数,若对于任意的
,任意的
,任意有限子集
,,且
,存在非零投射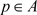 及A的C*-子代数
,且
,满足以下条件:
及A的C*-子代数
,且
,满足以下条件:
(1) 任给
, ;
(2) 任给
, ;
(3)
。
则
。
证明. 首先证明
。因为D是A的稠密自伴子代数,所以对于任给
存在
使得
。由
上的函数演算知
,即
,再用一次
上的函数演算可知
,且
,所以由
的任意性知
。
任给
,任意的有限集
,,且
。取
使得
,由 [3] 引理2.8知,存在
, 满足引理2.8的条件,令
,不妨设
且
,由于
,所以对于上述
,分别存在
,使得
又因为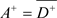 ,所以存在
,使得
且
。令
,由于D满足题设条件,所以对于
及上述
存在A的C*-子代数
以及非零投射
满足下列条件:
,所以存在
,使得
且
。令
,由于D满足题设条件,所以对于
及上述
存在A的C*-子代数
以及非零投射
满足下列条件:
(1) 任给
, ;
(2) 任给
, ;
(3)
。
所以对于任意的i,
(1')
.
(2') 因为对于任意的i,存在
,使
,,所以
同理
。故
,任意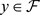 。
。
(3') 因为
,所以
,。
因此由 [4] 引理2.8知
即
因此
。
引理3.13. 设A为unital C*-代数,
,。设
,若存在
使得
,,则
其中
,。
证明. 因为
□
引理3.14. 设A为unital C*-代数,
,则
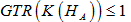 。
。
证明. 任意取定m,定义
上的投射
则
,所以
,因此可以将
看作是
的C*-子代数。
下面证明
。设I为
自身上的恒等算子,则
,且
为
的稠密自伴子代数。
对于任意
,,取 满足
,由 [3] 引理2.8知存在
, 满足引理2.8的条件,不妨设
。
满足
,由 [3] 引理2.8知存在
, 满足引理2.8的条件,不妨设
。
任意有限集
。其中
,,,,,,。
不妨设
,,,,,则
,,, 在范数拓扑下收敛。
令
,,。
且对于任意
,对每个
分别存在
,, 使得
当 时有,
时有,
令
设
则由引理3.13知
,。
不妨设
,若不然因为
,则由
上的函数演算知
,由此得
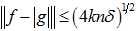 ,且因为
是
的C*-子代数知
,因此用
代替g即可。令
,则
为
的有限子集。
,且因为
是
的C*-子代数知
,因此用
代替g即可。令
,则
为
的有限子集。
因为
有单位元,所以
,因此
,所以对
以及上述
,,存在
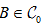 ,,,使
。
,,,使
。
满足:
(1) 任给
, ;
(2) 任给
, ;
(3)
。
则对任意
,任给
有
(1')
(2') 因为
,所以存在
使
,。则
同理因为
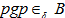 所以存在
使
,则
所以存在
使
,则
所以
,。
(3') 因为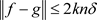 ,所以有
,所以有
所以由 [3] 引理2.8知
所以
由上述证明知
, 满足引理3.12的条件,所以可得
。
□
引理3.15. 设A是unital C*-代数,
,B是A的
-unital遗传C*-子代数则有
。
证明. 设
是B的一列近似单位,其中
。
对任意的
,有限集
,不妨设
,其中
。
选取
满足
,则由 [3] 引理2.8知存在
, 满足引理2.8的条件,不妨设
。
由于
是B的近似单位,所以对于
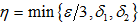 存在N使
存在N使
由B是A的遗传子代数易证
亦为A的unital遗传子代数。所以
。
对于
。由于
,所以对上述
,, 存在
,,,。
满足:
(1) 任给
, ;
(2) 任给
, ;
(3)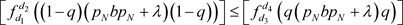 。
。
则
(1')
(2') 由(2)知对任给i,存在
使
则
(3') 由于
,所以
,所以
所以由 [3] 引理2.8知
所以
,即
。
□
定理3.16 设A为C*-代数,
,E是HAM。若
是
-unital的紧算子理想,则
。
证明. 因为
,且
,所以不妨设A是unital的。
因为
是
-unital的紧算子理想,所以E是可数生成的HAM。则由 [6] 定理15.4.6知
,所以
是
的遗传子代数。若
(1)
是unital紧算子理想,则由引理3.9以及定理3.14知
。
(2)
是
-unital的紧算子理想,则由引理
。
文章引用
刘晨晨. C*-代数的广义迹秩
The Generalized Tracial Rank of C*-Algebra[J]. 理论数学, 2020, 10(04): 307-317. https://doi.org/10.12677/PM.2020.104039
参考文献
- 1. Lin, H. (2001) The Tracial Topological Rank of C*-Algebras. Proceedings of the London Mathematical Society, 83, 199-234. https://doi.org/10.1112/plms/83.1.199
- 2. Gong, G., Lin, H. and Niu, Z. (2019) A Classification of Finite Simple Amenable Z-Stable C*-Algebras, I: C*-Algebras with Generalized Tracial Rank One. arXiv:1909.13382 [math.OA]
- 3. Hu, S., Lin, H. and Xue, Y. (2004) The Tracial Topological Rank of Extensions of C*-Algebras. Mathematica Scandinavica, 94, 125-147. https://doi.org/10.7146/math.scand.a-14433
- 4. Lin, H. (2001) An Introduction to the Classification of Amenable C*-Algebras. World Scientific, Singapore: https://doi.org/10.1142/4751
- 5. 魏常果, 王利广. 遗传子代数与正元的比较[J]. 中国科学: A辑, 2009(10): 1261-1266.
- 6. Wegge-Olsen, N. (1993) K-Theory and C*-Algebras. Oxford University Press, Oxford, New York, Tokyo.






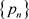 是A的近似单位,则称A是
-unital的。
是A的近似单位,则称A是
-unital的。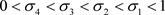 ,
以及任意有限集
,其中
,
以及任意有限集
,其中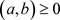 ,所以
。令
,,则由
知对上述
, 分别存在
,
,所以
。令
,,则由
知对上述
, 分别存在
,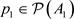 ,
, ,
满足:
,
满足: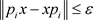 ;
;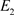 是有限维代数,
,,是
, 从
到
的同态且
,则
是有限维代数,
,,是
, 从
到
的同态且
,则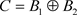 ,且
,所以
,且
,所以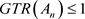 ,则
。
,则
。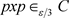 ;
;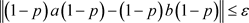 ,且因为
,
,且因为
,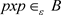 ;
;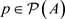 有
。
有
。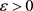 ,
,令
,
,
,令
,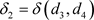 ,
,令
,
,
,令
,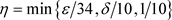 。
。 。
。 。
。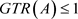 当且仅当
。
当且仅当
。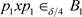 ;
;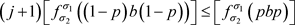 。
。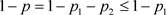 ,所以
,则由 [5] 定理3.3知
,所以
综上得
。
,所以
,则由 [5] 定理3.3知
,所以
综上得
。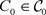 ,
,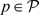 ,
,满足:
,
,满足: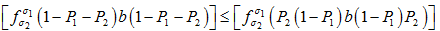 。
。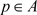 及A的C*-子代数
,且
,满足以下条件:
及A的C*-子代数
,且
,满足以下条件: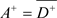 ,所以存在
,使得
且
。令
,由于D满足题设条件,所以对于
及上述
存在A的C*-子代数
以及非零投射
满足下列条件:
,所以存在
,使得
且
。令
,由于D满足题设条件,所以对于
及上述
存在A的C*-子代数
以及非零投射
满足下列条件: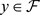 。
。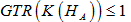 。
。 满足
,由 [3] 引理2.8知存在
, 满足引理2.8的条件,不妨设
。
满足
,由 [3] 引理2.8知存在
, 满足引理2.8的条件,不妨设
。 时有,
时有,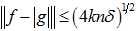 ,且因为
是
的C*-子代数知
,因此用
代替g即可。令
,则
为
的有限子集。
,且因为
是
的C*-子代数知
,因此用
代替g即可。令
,则
为
的有限子集。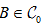 ,,,使
。
,,,使
。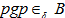 所以存在
使
,则
所以存在
使
,则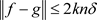 ,所以有
,所以有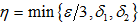 存在N使
存在N使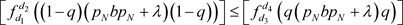 。
。