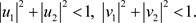Pure Mathematics
Vol.
13
No.
08
(
2023
), Article ID:
70315
,
9
pages
10.12677/PM.2023.138234
一类无界域的陆启铿问题
刘健,钟雨玲,胡琼方,杨尧,谢兵,冯志明*
乐山师范学院数理学院,四川 乐山
收稿日期:2023年6月29日;录用日期:2023年7月31日;发布日期:2023年8月7日

摘要
陆启铿问题指的是一个域D是否是陆启铿域,陆启铿域是对所有的
,Bergman核
都不等于零的域。本文讨论了一类无界域
的陆启铿问题。
关键词
Bergman核,陆启铿问题

Lu Qi-Keng’s Problem on Some Unbounded Domains
Jian Liu, Yuling Zhong, Qiongfang Hu, Yao Yang, Bing Xie, Zhiming Feng*
School of Mathematics and Physics, Leshan Normal University, Leshan Sichuan
Received: Jun. 29th, 2023; accepted: Jul. 31st, 2023; published: Aug. 7th, 2023

ABSTRACT
The Lu Qi-keng problem refers to whether a domain D is a Lu Qi-keng domain. The Lu Qi-keng domain is a domain where all
, and its Bergman kernel
are not equal to zero. In this paper, we investigate the Lu Qi-Keng problem for unbounded domains
.
Keywords:Bergman Kernels, Lu Qi-Keng Problem

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
假定
中的域,定义D上平方可积解析函数空间
这里
,
表示D上解析函数全体,
表示Lebesgue测度。如果
,记空间
的标准正交基为
,称
为域D的Bergman核,Bergman核在 中具有再生性,即对任意
,有
中具有再生性,即对任意
,有
对于包含原点的Reinhardt域D,D上解析函数有以下幂级数表示:
这里
,
,
。并且
是
的标准正交基,因此 [1]
Bergman核在多复变函数论和复几何中起着重要的作用,虽然
中的有界域都存在Bergman核,但其表达式一般没有显示公式,用显式公式计算Bergman核函数是多复变函数论的一个重要研究方向,用Bergman核的显示表达式,可以研究域的陆启铿问题,所谓陆启铿问题指的是一个域是否是陆启铿域,陆启铿域是对所有的
,Bergman核
都不等于零的域,如果一个域是陆启铿域,则它的表示域存在 [2] 。关于Bergman核的计算,可参考综述文献 [3] [4] ,有界域的陆启铿问题研究可参考综述文献 [5] ,近期这方面的研究可参考 [6] [7] [8] [9] 等。在 [7] 和 [9] 中研究了一类无界域——Fock-Bargmann-Hartogs域
的陆启铿问题,本文我们研究另一类无界域(定义见(2.1))的Bergman核的计算,并研究其陆启铿问题。
2. 主要结果
定理2.1. 令
,
(2.1)
则域D的Bergman核为
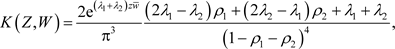 (2.2)
(2.2)
其中
由定理2.1,我们得到以下结论。
定理2.2. 在定理2.1的假设下,则域D的Bergman核
在
上有零点的充要条件是
。
3. 定理2.1的证明
证明. 记
这里
,
表示D上解析函数全体,
表示Lebesgue测度。对于包含原点的Reinhardt域D上的全纯函数f,在D上有幂级数展开式(见 [1] )
这里
容易直接证明
是Reinhardt域上的一组规范正交系,可以证明它是完备的。因而有
其中
直接计算得

上面用到
以及

这里用到

所以当
时
这里
。
由于
于是有
记
这里
根据
得
因此
证毕
4. 定理2.2的证明
为了研究定理2.1中域D的陆启铿问题,我们先给出以下结论。
定理4.1. 在定理2.1的条件下,以下结论成立:
(i) 如果
,那么
(4.1)
(ii) 如果
和
,则存在
,使得
和
。
证明. (i) 由于
同样得
其中
于是由不等式
得
再根据
得
同样得
(ii) 令
,则
,并且
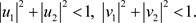
如果
和
至少有一个为零,则结论成立。以下假定
,并证明关于
的不等式组
(4.2)
有解。
令
,则上面不等式组(4.2)等价于
进一步化简得
于是不等式组(4.2)有解等价于不等式组
有解。容易验证当
时,
是它的解。证毕
现在给出定理2.2的证明。
定理2.2的证明。(i) 当
时,有
因
所以
(ii) 当
时,有
由此得
(iii) 当
时,如果
,根据(2.2)有
(4.3)
令
,则
根据
得不等式组
(4.4)
关于
有解。
记
则
的解为
的解为
(iii-1) 当
时,令
的解为
的解为
此时不等式
的解为
不等式
的解为
这表明不等式组(4.4)有解
当
时,有
,根据定理4.1得
在
内有解。
(iii-2) 当
时,如果不等式组(4.4)有解,则
不可能是(4.4)的解,这是因为
于是解
满足以下条件
(4.5)
这里
由(4.5)可知
这等价于
进一步化简得
这和条件
矛盾。因此在
时,对一切
,Bergman核
。证毕
致谢
大学生创新创业训练计划项目(No: S202210649222)。
文章引用
刘 健,钟雨玲,胡琼方,杨 尧,谢 兵,冯志明. 一类无界域的陆启铿问题
Lu Qi-Keng’s Problem on Some Unbounded Domains[J]. 理论数学, 2023, 13(08): 2275-2283. https://doi.org/10.12677/PM.2023.138234
参考文献
- 1. 史济怀. 多复变函数论基础[M]. 北京: 高等教育出版社, 2014.
- 2. 陆启铿. 关于常曲率的Kähler流形[J]. 数学学报, 1966, 16(2): 269-281.
- 3. 殷慰萍. 有界域的Bergman核函数显示表示的最新进展[J]. 数学进展, 2002, 31(4): 295-312.
- 4. 殷慰萍. 华罗庚域研究的综述[J]. 数学进展, 2007, 36(2): 129-152.
- 5. 殷慰萍. 中有界域的Bergman核函数的零点问题[J]. 数学进展, 2008, 37(1): 1-14.
- 6. Zhang, L. and Yin, W. (2009) Lu Qi-Keng’s Problem on Some Complex Ellipsoids. Journal of Mathematical Analysis and Applications, 357, 364-370. https://doi.org/10.1016/j.jmaa.2009.04.018
- 7. Yamamori, A. (2013) The Bergman Kernel of the Fock-Bargmann-Hartogs Domain and the Polylogarithm Function. Complex Variables and Elliptic Equations, 58, 783-793. https://doi.org/10.1080/17476933.2011.620098
- 8. Hao, Y.H. and Wang, A. (2015) The Bergman Kernels of Generalized Bergman-Hartogs Domains. Journal of Mathematical Analysis and Applications, 429, 326-336. https://doi.org/10.1016/j.jmaa.2015.04.023
- 9. Dai, J. and Li, Y. (2022) The Bergman Kernel and Projection on the Fock-Bargmann-Hartogs Domain. Complex Variables and Elliptic Equations, 67, 34-48. https://doi.org/10.1080/17476933.2020.1816982
NOTES
*通讯作者。






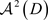 中具有再生性,即对任意
,有
中具有再生性,即对任意
,有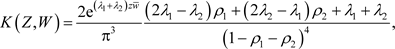 (2.2)
(2.2)