ABSTRACT

Starting from the simple Schmidt orthogonalization in mathematics, the coordinate transformation in physics is taken as the key point, and the concept of tensor is introduced simply without losing mathematical rigor and physical significance, and the operation of tensor is introduced. The purpose is to reduce the difficulty of tensor teaching in senior and graduate students of physics department.

Keywords:Tensor, Schmidt Orthogonalization, Coordinate System Transformation

张量概念的一种简单引入

李恩辉¹，宿非凡²

¹中国人民大学附属中学，北京

²中国科学院物理研究所，北京

收稿日期：2019年10月30日；录用日期：2019年11月15日；发布日期：2019年11月22日

摘 要

从数学上简单的施密特正交化出发，把物理上的坐标变换作为重点，既不失数学严谨又不失物理意义地简单引入张量的概念并对张量的运算做了一些介绍。旨在降低目前物理系高年级和研究生中张量教学的难度。

关键词 :张量，施密特正交化，坐标系变换

Copyright © 2019 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 前言

在自然界中，严格的说我们的物理量大多数都是张量。在初等物理中最为常见的是零阶张量——标量和一阶张量——矢量。而在高等物理中仅仅有标量和矢量的概念是远远不够的，例如在研究各向异性的电介质极化，相对论电动力学和量子场论一般理论时应用标量和矢量都不能正确描述理论体系的物理实际特征，所以引入高阶张量势在必行 [1]。

2. 施密特正交化与张量概念的引入

在目前我国高校物理系各个专业的本科高年级和研究生教学中，张量这部分知识有一些教学版本，但是从学生的角度来看，对物理专业学生仍需要一个数学意义明显，物理意义突出的简单教案，本文就在这方面做出一些努力，试图用较小的篇幅向物理系需要将张量当做学习高等物理工具的同学介绍清楚张量的基本概念和物理上的意义。力图帮助同学们扫清在学习中遇到的数学困难，使得量子场论，相对论量子力学等高等物理课程的教学达到更好的效果。

从张量的物理意义上来看，某个张量除了自身数学上的基本概念之外还应该包含坐标变换的规律以显示其物理意义。以下从最熟悉的直线坐标系的一阶张量入手，扩展到一般的曲线坐标系，最后从一般曲线坐标系的施密特正交化自然地导出张量的严格定义。

先来讨论直线坐标系的一阶张量，对于最简单的直线坐标系而言，任意三个线性无关的矢量 $e_1$ 、 $e_2$ 、 $e_3$ 都可以作为基矢量，需注意对于普遍的情况它们不一定正交也不一定归一。所以，为了方便地研究物理问题不妨定义另一组线性无关的矢量 $e^1$ 、 $e^2$ 、 $e^3$ 使之与基矢量 $e_1$ 、 $e_2$ 、 $e_3$ 分别对应正交归一，这组基矢量称为原基矢量的共轭基矢量。

在基本的线性代数理论中，施密特正交化的方法是构造这种矢量的标准方法，故定义：

$e^1=\frac{e_2\times e_3}{e_1\cdot \left(e_2\times e_3\right)}$

$e^2=\frac{e_3\times e_1}{e_1\cdot \left(e_2\times e_3\right)}$

$e^3=\frac{e_1\times e_2}{e_1\cdot \left(e_2\times e_3\right)}$

不难验证如此定义使得： $e^i\cdot e_j={\delta }_j^i=\{\begin{array}{l}1\left(i=j\right)\\ 0\left(i\ne j\right)\end{array}$

这样一来就称矢量 $e^1$ 、 $e^2$ 、 $e^3$ 分别为基矢量 $e_1$ 、 $e_2$ 、 $e_3$ 的共轭基矢量。可见，由于 $e_1$ 、 $e_2$ 、 $e_3$ 不一定正交归一，其共轭基矢量 $e^1$ 、 $e^2$ 、 $e^3$ 也不一定正交归一。在常见的笛卡尔直角坐标系中 $e_1$ 、 $e_2$ 、 $e_3$ 正交归一，此时由上面的定义式可知 $e^1$ 、 $e^2$ 、 $e^3$ 分别与 $e_1$ 、 $e_2$ 、 $e_3$ 大小相等方向相同。所以，在一般的笛卡尔直角坐标系中我们不做任何区分。

从数学上知道，任何一个矢量都可以表示成为分量的形式，即可以表示成为：

$k=a{e}_1+b{e}_2+c{e}_3$ (1)

根据定义 $e^i\cdot e_j={\delta }_j^i$，可以得到：

$k\cdot e^1=a{e}^1\cdot e_1=a$

$k\cdot e^2=b{e}^2\cdot e_2=b$

$k\cdot e^3=c{e}^3\cdot e_3=c$

所以得到：

$k=\left(k\cdot e^1\right)e_1+\left(k\cdot e^2\right)e_2+\left(k\cdot e^3\right)e_3$

$\Rightarrow$ $k=k^1{e}_1+k^2{e}_2+k^3{e}_3$ (2)

根据爱因斯坦求和约定上式可以表达为：

$k=k^i{e}_i$ (3)

其中 $k^i$ 定义为矢量 $k$ 的协变分量。在下面可以看到协变分量的具体定义。

同样地也可以得到： $k=k^j{e}_j$，也就是说任何一个矢量 $k$ 在坐标系中可以分别用其基矢量和其共轭矢量表示。

既然在同一个坐标系中矢量可以用基矢量和共轭基矢量来表示，很自然的就要将其拓展到不同的坐标系之下。为了清晰的展示不同的矢量在坐标变换下的规律以下分别讨论基矢量和共轭基矢量的坐标变换关系。

利用定义 $e^i\cdot e_j={\delta }_j^i$ 可以很快地得到不同坐标系之间的关系式：

${e^{\prime }}_i=\left({e^{\prime }}_i\cdot e^j\right)e_j={\beta }_i^j{e}_j$ (4)

${x^{\prime }}_i=\left(x_j{e}^j\right)\cdot {e^{\prime }}_i=\left({e^{\prime }}_i\cdot e^j\right)x_j={\beta }_i^j{x}_j$ (5)

(其中 ${\beta }_i^j={e^{\prime }}_i\cdot e^j$ )

其共轭矢量满足：

${e^{\prime }}^i=\left({e^{\prime }}_i\cdot e_j\right)e^j={\left({\beta }^{-1}\right)}_j^i{e}^j$ (6)

${x^{\prime }}^i=\left(x^j{e}_j\right)\cdot {e^{\prime }}^i=\left({e^{\prime }}^i\cdot e_j\right)x^j={\left({\beta }^{-1}\right)}_j^i{x}^j$ (7)

可见分量 $x_i$ 在坐标变换下与基矢量 $e_i$ 一样服从协变变换规律，所以称其为“协变分量”；而分量 $x^i$ 在坐标变换中与基矢量 $e^i$ 一样服从逆变变换规律，故称其为“逆变分量”。

至此，我们讨论了一般的直线坐标系中的基矢量与共轭基矢量所满足的一些规律。更加一般地，在曲线坐标系中以三维空间为例，任何一个矢量在曲线坐标系都可以记为：

$r=r\left(y^1,y^2,y^3\right)=y^i{\epsilon }_i$

在熟悉的笛卡尔坐标系中有：

$r=r\left(y^1,y^2,y^3\right)=x^i{e}_i$

在笛卡尔坐标系的 $r$ 处，矢量的无穷小增量可以记为：

$\text{d}r=\frac{\partial r}{\partial y^i}\text{d}{y}^i=\left(\frac{\partial x^j}{\partial y^i}{e}_j\right)\text{d}{y}^i$

故可将基矢量 ${\epsilon }_i$ 和其共轭基矢量 ${\epsilon }^i$ 选为：

${\epsilon }_i=\frac{\partial r}{\partial y^i}=\frac{\partial x^j}{\partial y^i}{e}_j$ (8)

${\epsilon }^i=\nabla y^i=\frac{\partial y^i}{\partial x^j}{e}_j$ (9)

可以验证上式满足：

${\epsilon }_i\cdot {\epsilon }^k=\frac{\partial x^j}{\partial y^i}{e}_j\cdot \frac{\partial y^k}{\partial x^l}{e}_l=\frac{\partial x^j}{\partial y^i}\frac{\partial y^k}{\partial x^l}{e}_j\cdot e_l=\frac{\partial x^j}{\partial y^i}\frac{\partial y^k}{\partial x^l}{\delta }_{jl}=\frac{\partial x^j}{\partial y^i}\frac{\partial y^k}{\partial x^j}={\delta }_i^k$

即： ${\epsilon }_i\cdot {\epsilon }^j={\delta }_i^k$，即二者正交归一，符合初始定义。

对于一般的曲线坐标系来说，基矢量 ${\epsilon }_i$ 和共轭基矢量 ${\epsilon }^i$ 都是 $x_i$ 的函数，不同的点的基矢量和共轭基矢量的大小、方向都有可能不相同，量纲一般也不同，这时必须考虑基矢量对坐标的微商的非零贡献。这时通常选取与前面相同的自然基： [2]

${\epsilon }_i=\frac{\partial r}{\partial y^i}$，${\epsilon }^i=\frac{\partial r}{\partial y_i}$ (10)

对于不同的坐标系，应该分别作相应的计算。详细的计算例子参见相关文献 [3] [4]。

在做好了上述的准备之后，就可以来讨论张量的普遍定义。在物理中常见的张量有如下几种。

1) 零阶张量：零阶张量有 $n^0=1$ 个元素且其数值与坐标变换无关，即： ${\varphi }^{\prime }=\varphi$。例如基础物理中的时间t，其不随坐标变换而发生变化。

2) 一阶张量：一阶张量有 $n^1=n$ 个元素，在坐标变换下分为一阶协变张量与一阶逆变张量

协变张量： ${T^{\prime }}_i=\frac{\partial y^j}{\partial {y^{\prime }}^i}{T}_j={\beta }_i^j{T}_j$

逆变张量： ${T^{\prime }}^i=\frac{\partial {y^{\prime }}^i}{\partial y^j}{T}^j={\left({\beta }^{-1}\right)}_j^i{T}^j$

例如位移 $s$，力 $F$ 等物理量。其在坐标变换下只保有原来的分量个数，这在数学上表示为其只有 $n^1=n$ 个元素。

3) 二阶张量：二阶张量有 $n^2$ 个元素，在坐标变换下分为二阶协变张量，二阶逆变张量与二阶混合张量。

协变张量： ${T^{\prime }}_{ij}=\frac{\partial y^k}{\partial {y^{\prime }}^i}\frac{\partial y^l}{\partial {y^{\prime }}^j}{T}_{kl}={\beta }_i^k{\beta }_l^j{T}_{kl}$

逆变张量： ${T^{\prime }}^{ij}=\frac{\partial {y^{\prime }}^i}{\partial y^k}\frac{\partial {y^{\prime }}^j}{\partial y^l}{T}^{kl}={\left({\beta }^{-1}\right)}_k^i{\left({\beta }^{-1}\right)}_l^j{T}^{kl}$

混合张量： $\{\begin{array}{l}{T^{\prime }}_j^i=\frac{\partial {y^{\prime }}^i}{\partial y^k}\frac{\partial y^l}{\partial {y^{\prime }}^j}{T}_l^k={\left({\beta }^{-1}\right)}_k^i{\beta }_j^l{T}_l^k\\ {T^{\prime }}_i^j=\frac{\partial y^k}{\partial {y^{\prime }}^i}\frac{\partial {y^{\prime }}^j}{\partial y^l}{T}_k^l={\beta }_i^k{\left({\beta }^{-1}\right)}_l^j{T}_k^l\end{array}$

例如各向异性的介电常数 ${\epsilon }_{ij}$，相对论能动量 $P_{ij}$ 以及工程上常见的应力和应变。这些量的作用效果没有特定的方向性。

4) 高阶张量：有 $n^{p+q}$ 个元素，在一般物理理论之中不常用，故这里从略。

这里需要指明的是，为了突出张量坐标变换的性质我们定义 $g_{ij}={\epsilon }_i\cdot {\epsilon }_j$ 为二阶协变度规张量， $g^{ij}={\epsilon }^i\cdot {\epsilon }^j$ 为二阶逆变度规张量，这个度规张量就是刻画空间的主要性质的量。

最后，介绍一些物理学中常用的张量代数运算。对于张量的运算，我们定义其加减运算为：

$C_{i_1{i}_2\cdots i_p}^{j_1{j}_2\cdots j_p}=A_{i_1{i}_2\cdots i_p}^{j_1{j}_2\cdots j_p}\pm B_{i_1{i}_2\cdots i_p}^{j_1{j}_2\cdots j_p}$

从定义式可以看出，只有阶数相同的且协变、逆变指标的个数、顺序都完全相同的张量才可以相加减。这是因为从物理意义上来看，只有在坐标上的同一个点的物理量才可以相加减，也就是说只有完全相同的张量才可以相加减。

除了张量的加减我们还对协变和逆变分量之间的关系感兴趣，以下我们就来讨论这个问题 [4]。

$\because {\epsilon }^i={\epsilon }^i\left({\epsilon }^j\cdot {\epsilon }_j\right)=\left({\epsilon }^i\cdot {\epsilon }^j\right){\epsilon }_j=g^{ij}{\epsilon }_j$

${\epsilon }_i={\epsilon }_i\left({\epsilon }_j\cdot {\epsilon }^j\right)=\left({\epsilon }_i\cdot {\epsilon }_j\right){\epsilon }^j=g_{ij}{\epsilon }^j$

$A^i=A\cdot {\epsilon }^i=g^{ij}A\cdot {\epsilon }_j=g^{ij}{A}_j$

$A_i=A\cdot {\epsilon }_i=g_{ij}A\cdot {\epsilon }^j=g_{ij}{A}^j$

$\therefore$ 度规张量 $g_{ij}$ 可以用于协变与逆变分量的相互转化。这一点并不奇怪，从度规的定义上来看我们可以形象的认为度规是刻画两个空间几何关系的一个张量，所以当然可以将协变量“换算”为逆变量。

这样一来，任何两个坐标中的量均可以相互转化。所以说在物理学中引入张量，使得物理学的研究可以在任意的坐标系中相互转化。

特别的，在同一个最一般的坐标系中，矢量的内积的普适表达式可以用张量来表述：

$A\cdot B=A^i{\epsilon }_i\cdot B^j{\epsilon }_j=A^i{B}^j{g}_{ij}=A^i{B}_j$ (11)

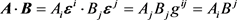或： (12)

这里就得出了一个张量运算中常用的结论：

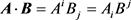(13)

对于高阶张量指标的升降有：

，

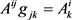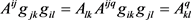
3. 结论

本文从数学上基本的坐标系施密特正交化出发，以物理上坐标系变换的概念为重点。数学上简单、系统地介绍了高等物理系课程需要的张量内容。既不失数学的严谨，又不失物理意义，有益于物理系研究生和高年级本科生的张量简单教学。

文章引用

李恩辉,宿非凡. 张量概念的一种简单引入
A Simple Way to Introduce the Concept of Tensor[J]. 现代物理, 2019, 09(06): 343-347. https://doi.org/10.12677/MP.2019.96032

参考文献