Computer Science and Application
Vol.06 No.09(2016), Article ID:18637,10
pages
10.12677/CSA.2016.69071
The Algorithms for the Hamiltonian Decomposition of the General Cube-Connected Cycles Network
Haizhong Shi, Liting Chang
College of Mathematics and Statistics,

Received: Sep. 9th, 2016; accepted: Sep. 24th, 2016; published: Sep. 29th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The cube-connected cycles network is a hypercube of bounded-degree derivative. It has almost all of the excellent properties of hypercube. It also overcomes the shortcoming of hypercube vertices of degrees which will increase with the augment of the network size. But the cube-connected cycles network is simple or complex? This is an open question. Chordal ring network is a kind of classical interconnection network, which has the advantages of simple structure and so on. In this article, a model of the regular graph connected cycle network which is proposed by Haizhong Shi is used to design a kind of network which contains the cube-connected cycles network—the generalized cube-connected network GCCC(n) (n > 2). The authors prove that GCCC(n) (n > 2) can be decomposed into union of edge-disjoint a Hamiltonian cycle and a perfect matching, namely, GCCC(n) (n > 2) is a chordal ring network. They also make a algorithm for GCCC(n) (n > 2) can be decomposed into union of edge-disjoint a Hamiltonian cycle and a perfect matching.
Keywords:Interconnection Network, General Cube-Connected Cycles, Hamiltonian Cycle, Perfect Matching, Chordal Ring Network

推广立方连通圈网络的Hamilton分解的算法
师海忠,常立婷
西北师范大学数学与统计学院,甘肃 兰州

收稿日期:2016年9月9日;录用日期:2016年9月24日;发布日期:2016年9月29日

摘 要
立方连通圈网络是超立方体的有界度变形,它具有超立方体几乎所有的优良性质,而且克服了超立方体顶点度随网络规模增大而增大的缺点,是代替超立方体的一个具有强大竞争力的网络结构。但立方连通圈网络的结构是简单还是复杂呢?这是一个悬而未决的问题。带弦环网络是一类经典的互连网络,该网络具有结构简单等优点。在这篇文章中利用师海忠提出的正则图连通圈网络模型设计出了包含立方连通圈网络的一类网络——推广立方连通圈网络GCCC(n) (n > 2),证明了GCCC(n) (n > 2)可分解为边不交的一个Hamilton圈和一个完美对集的并,即GCCC(n) (n > 2)是带弦环网络。并给出推广立方连通圈网络分解为边不交的一个Hamilton圈和一个完美对集的并的算法。
关键词 :互连网络,推广立方连通圈,Hamilton圈,完美对集,带弦环网络

1. 引言
互连网络是超级计算机的重要组成部分,互连网络通常模型化为一个图,图的顶点对应处理机,图的边对应通信全过程。各种已有互连网络参见 [1] - [18] 。立方连通圈网络是由Preparate和Vailemin [19] 首先提出并研究的,它具有超立方体几乎所有的优良性质,而且克服了超立方体大顶点度的缺点。它是三连通三正则图,而且是Hamilton图(详细参见 [20] - [25] )。
推广立方连通圈网络GCCC(n) (n > 2) (见定义3)是含有立方连通圈网络的一簇网络,它是三正则的,有 个顶点和
个顶点和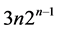 条边,这篇文章中提出了推广立方连通圈网络的概念,并证明了推广立方连通圈网络可分解为边不交的Hamilton圈和一个完美对集的并,即GCCC(n) (n > 2)是带弦环网络。并给出了推广立方连通圈网络分解为边不交的Hamilton圈和一个完美对集的并的算法。本文的其它结构为:2基本概念,3推广立方连通圈网络的Hamilton分解的算法,4案例举证,5结束语。
条边,这篇文章中提出了推广立方连通圈网络的概念,并证明了推广立方连通圈网络可分解为边不交的Hamilton圈和一个完美对集的并,即GCCC(n) (n > 2)是带弦环网络。并给出了推广立方连通圈网络分解为边不交的Hamilton圈和一个完美对集的并的算法。本文的其它结构为:2基本概念,3推广立方连通圈网络的Hamilton分解的算法,4案例举证,5结束语。
2. 基本概念
2.1. 推广立方连通圈网络的定义
定义1 [5] :n-立方体 定义如下无向图
定义如下无向图

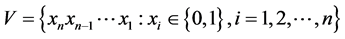

定义2 [5] :CCC(n)定义如下
顶点集 ,两顶点
,两顶点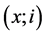 和
和 由一条无向边相连当且仅当,或者
由一条无向边相连当且仅当,或者
(i) 且
且 ,或者
,或者
(ii)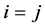 且
且 和
和 恰有第
恰有第 个指标不同。
个指标不同。
定义3:用一个圈代替立方体 中的每个顶点,且每个圈中顶点恰位于立方体
中的每个顶点,且每个圈中顶点恰位于立方体 中与该顶点关联的一条边上,得到的新的网络叫做推广立体连通圈网络,记作GCCC(n)。
中与该顶点关联的一条边上,得到的新的网络叫做推广立体连通圈网络,记作GCCC(n)。
2.2. 正则图G的Hamilton分解
定义4 [26] :设 是正则图,
是正则图, 是
是 的边集.我们称
的边集.我们称 是Hamilton可分解的。如果
是Hamilton可分解的。如果
要么
(i) 且
且 能被划分成
能被划分成 个Hamilton圈;
个Hamilton圈;
要么
(ii) 且
且 能被划分成
能被划分成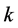 个Hamilton圈和一个完美对集;
个Hamilton圈和一个完美对集;
这里 表示
表示 的顶点度。
的顶点度。
2.3. 推广立方连通圈网络的Hamilton分解
定义5 [27] :设 是一个图,
是一个图, 的Euler回是指经过每条边恰好一次的回。
的Euler回是指经过每条边恰好一次的回。
定义6 [27] :一个图若包含Euler回,则称这个图为Euler图。
定理1: 有Euler回路。
有Euler回路。
引理1 [27] :一个非空连通图是Euler图当且仅当该图的每个顶点度均为偶数。
给定 的完美对集
的完美对集

我们有

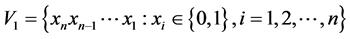

定理2: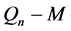 是连通的。
是连通的。
证明:当 时
时 ,此时
,此时
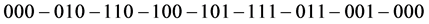 是
是 中的圈,故
中的圈,故 连通。
连通。
假设当 时,
时, 连通,即对
连通,即对 有
有
 路,则
路,则
当 时,
时,
由 有
有 路知
路知
对 有
有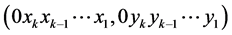 路;
路;
对 有
有 路;
路;
对 有
有 路;
路;
对 有
有 路。
路。
综上所述
对 有
有 路,即
路,即 连通。
连通。
由数学归纳法知 连通。
连通。
定理3:当 为奇数时,
为奇数时,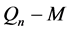 (
( )是Euler图。
)是Euler图。
定理4 [28] :2r-正则图连通圈网络是Hamilton可分解的。
定理5:(1) GCCC(2r)是Hamilton可分解的;(2) GCCC(2r)是带弦环网络。
由定理2~5得:
推论1:(1) GCCC(2r + 1)可分解为边不交的一个Hamilton圈和一个完美对集的并,即GCCC(2r + 1)是Hamilton可分解的;(2) GCCC(n) (2r + 1)是带弦环网络。
3. 推广立方连通圈网络的Hamilton分解的算法
算法:
输入 (
( )
)
If 为偶数
为偶数
Then
{
1) let 
2) 运用Fleury算法 [26] 找到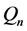 的一个Euler回路
的一个Euler回路
3) 对顶点 ,找到其关联的
,找到其关联的 条边在Euler回路中配成的相邻的
条边在Euler回路中配成的相邻的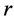 对,记为
对,记为 ,
, ,且
,且 ,用标号为
,用标号为 的圈
的圈 代替
代替 ,其中
,其中 与
与 (
( )关联。
)关联。 中嵌入
中嵌入 后得到GCCC(n) ,Euler回路中嵌入
后得到GCCC(n) ,Euler回路中嵌入
 后得到GCCC(n)的一个Hamilton圈,其于边构成GCCC(n) 的一个完美对集。转7
后得到GCCC(n)的一个Hamilton圈,其于边构成GCCC(n) 的一个完美对集。转7
}
Else
{
4) let 
5) 运用Fleury算法找到 的一个Euler回路
的一个Euler回路
6) 对顶点 ,找到其关联的
,找到其关联的 条边在Euler回路中配成的相邻的
条边在Euler回路中配成的相邻的 对,记为
对,记为 ,
, ,且
,且 ,用标号为
,用标号为 的圈
的圈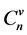 代替
代替 ,其中
,其中 与
与 (
( )关联,
)关联, 与
与 中的边关联。
中的边关联。 中嵌入
中嵌入 后得到GCCC(n),Euler回路中嵌入
后得到GCCC(n),Euler回路中嵌入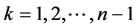
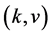 及
及 后得到GCCC(n)的一个Hamilton圈,其于边构成GCCC(n)的一个完美对集。转7
后得到GCCC(n)的一个Hamilton圈,其于边构成GCCC(n)的一个完美对集。转7
}
7) 输出GCCC(n)及它的Hamilton圈和完美对集,结束。
4. 案例举证
4.1. n = 3时的情形
当n = 3时,输入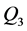 (如图1所示)
(如图1所示)
由Fleury算法得到的Euler回路为:

输出的GCCC(3)如图2所示
输出的Hamilton圈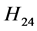 为:
为:

Figure 1. Q3
图1. Q3

Figure 2. GCCC(3)
图2. GCCC(3)
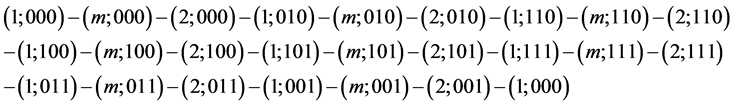
输出的完美对集 为:
为:
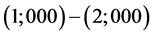 ;
;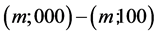 ;
; ;
;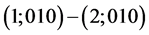 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;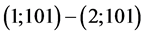 。
。
此时由 和
和 得到的图如图3所示
得到的图如图3所示
把上述Hamilton圈 记为:
记为:

得到相应的完美对集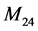 为:
为:
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;
 ;
; 。
。
4.2. n = 4时的情形
当n = 4时,输入 (如图5所示)
(如图5所示)
由Fleury算法得到的Euler回路为:


Figure 3. Figure constituted by the H24 and M24
图3. 由H24和M24构成的图
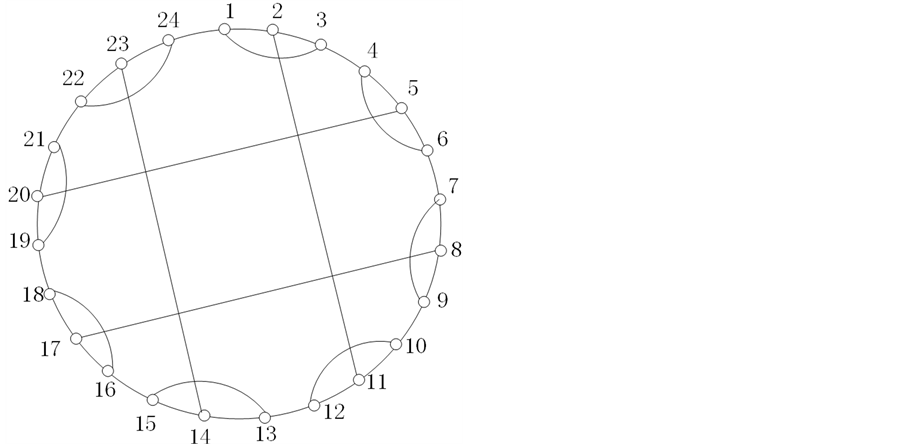
Figure 4. GCCC(3) corresponding to Chordal ring network
图4. GCCC(3)对应的带弦环网络

Figure 5. Q4
图5. Q4
输出的GCCC(4)如图6所示
输出的Hamilton圈 为:
为:

输出的完美对集 为:
为:
 ;
; ;
; ;
; ;
;
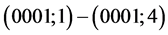 ;
;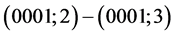 ;
; ;
; ;
;
 ;
;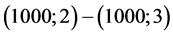 ;
; ;
; ;
;
 ;
; ;
; ;
;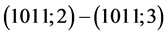 ;
;
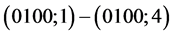 ;
;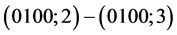 ;
; ;
; ;
;
 ;
;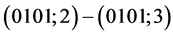 ;
; ;
; ;
;
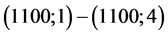 ;
;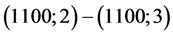 ;
; ;
; ;
;
 ;
; ;
;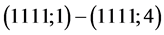 ;
; 。
。
把上述Hamilton圈 记为:
记为:

得到的相应的完美对集 为:
为:
 ;
; ;
; ;
; ;
; ;
; ;
; ;
;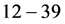 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;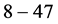 ;
; ;
;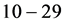 ;
; ;
; ;
;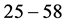 ;
; ;
; ;
;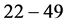 ;
; ;
; 。
。

Figure 6. GCCC(4)
图6. GCCC(4)

Figure 7. GCCC(4) corresponding to Chordal ring network
图7. GCCC(4)对应的带弦环网络
5. 结束语
推广立方连通圈网络GCCC(n) (n > 2)是包含立方连通圈的一类网络,文章中证明了GCCC(n) (n > 2)可分解为边不交的一个Hamilton圈和一个完美对集的并,即GCCC(n) (n > 2)是带弦环网络。并给出了推广立方连通圈网络分解为边不交的一个Hamilton圈和一个完美对集的并的算法。但对一般的CCC(n) (n > 2)由Fleury算法构造恰当的Euler回路,以便设计构造CCC(n) (n > 2)的Hamilton分解的算法有待进一步的研究。
文章引用
师海忠,常立婷. 推广立方连通圈网络的Hamilton分解的算法
The Algorithms for the Hamiltonian Decomposition of the General Cube-Connected Cycles Network[J]. 计算机科学与应用, 2016, 06(09): 573-582. http://dx.doi.org/10.12677/CSA.2016.69071
参考文献 (References)
- 1. Akers, S.B., Harel, D. and Krishnamurthy, B. (1987) The Star Graph: An Attractive Alternative to the n-Cube. Proceeding of the 1987 International conference on Parallel Processing, The Pennsylvania University Press, Philadelphia, 393-400.
- 2. Akers. S.B. and Krishnamurthy, B. (1989) A Group-Theoretic Model for Symmetric Interconnection Networks. IEEE Transactions on Computers, 38, 555-565. http://dx.doi.org/10.1109/12.21148
- 3. Ohring, S.R., Sarkar, F. and Hohndel, D.H. (1995) Cayley Graph Connected Cycles: A New Class of Fixed-Degree Interconnection Networks. Proceeding of the 28th annual Hawaii International Conference on System Science, 3-6 January 1995, 479-488. http://dx.doi.org/10.1109/hicss.1995.375509
- 4. 师海忠. 互连网络的代数环模型[D]: [博士学位论文]. 北京: 中国科学院应用数学研究所, 1998.
- 5. 徐俊明. 组合网络理论[M]. 北京: 科学出版社, 2007.
- 6. Efe, K. (1991) A Variation on the Hypercube with Lower Diameter. IEEE Transactions on Computer, 40, 1312-1316. http://dx.doi.org/10.1109/12.102840
- 7. Ei-Amawy, A. and Latifi, S. (1991) Properties and Performance of Folded Hypercubes. IEEE Transactions on Parallel and Distributed Systems, 2, 31-42. http://dx.doi.org/10.1109/71.80187
- 8. Cull, P. and Larson, S.M. (1995) The Mǒbius Cube. IEEE Transactions on Computer, 44, 647-659. http://dx.doi.org/10.1109/12.381950
- 9. Efe, K. (1998) The Crossed Cube Architecture for Parallel Computation. IEEE Transactions on Parallel and Distributed Systems, 3, 513-523. http://dx.doi.org/10.1109/71.159036
- 10. Hsu, L.-H. and Lin, C.-K. (2009) Graph Theory and Interconnection Networks. CRC Press, New York.
- 11. 师海忠. 正则图连通圈: 多种互连网络的统一模型[C]//中国运筹学会. 中国运筹学会第十届学术交流会论文集. Hong Kong: Global-link Informatics Limited, 2010: 202-208.
- 12. 师海忠, 牛攀峰, 马继勇, 侯菲菲. 互连网络的向量图模型[J]. 运筹学学报, 2011, 15(3): 115-123.
- 13. 师海忠, 路建波. 关于互连网络的几个猜想[J]. 计算机工程与应用, 2008, 44(31): 112-115.
- 14. 师海忠. 互连网络的新模型: 多部群论模型[J]. 计算机科学, 2013, 40(9): 21-24.
- 15. 师海忠. 几类新的笛卡尔乘积互连网络[J]. 计算机科学, 2013, 40(6A): 265-270.
- 16. Shi, H. and Shi, Y. (2015) A New Model for Interconnection Network: K-Hierarchical Ring and R-Layer Graph Network. http://vdisk.weibo.com/s/dlizJyferZ-Zl
- 17. Shi, H. and Shi, Y. (2010) A Hierarchical Ring Group-Theoretic Model for Intercon-nection Networks. http://vdisk.weibo.com/s/dlizJyfeBX-2J
- 18. Shi, H. and Shi, Y. (2015) Cell-Breading Graph Model for Interconnection Networks. http://vdisk.weibo.com/s/dlizJyfesb05y
- 19. Preparata, F.P. and Vuillemin, J. (1981) The Cube-Connected Cycles: A Versatile Network for Parallel Computation. Communications of the Association for Computing Machinery, 24, 300-309. http://dx.doi.org/10.1145/358645.358660
- 20. Annexstein, F., Baumslag, M. and Rosenberg, A.L. (1990) Group Action Graphs and Parallel Architectures, SIAM Journal on Computing, 19, 544-569. http://dx.doi.org/10.1137/0219037
- 21. Bruck, J., Cypher, R. and Ho, C.-T. (1995) On the Construction of Fault-Tolerant Cube-Connected Cycles Networks. Journal Parallel and Distributed Compu-ting, 25, 98-106. http://dx.doi.org/10.1006/jpdc.1995.1032
- 22. Friš, I., Havel, I. and Liebl, P. (1997) The Diameter of the Cube-Connected Cycles. Information Processing Letters, 61, 157-160. http://dx.doi.org/10.1016/S0020-0190(97)00013-6
- 23. Stong, R. (1987) On Hamiltonian Cycles in Cayley Graphs of Wreath Products. Discrete Mathematics, 65, 75-80. http://dx.doi.org/10.1016/0012-365X(87)90212-3
- 24. Miller, F.P. (2010) Cube-Connected Cycles. VDM Verlag Dr. Müller, Saarbrücken.
- 25. Li, H., Hsu, T.-H., Ho, Y.-H. and Tsay, C.-W. (2014) Cycles in Cube-Connected Graph. Discrete Applied Ma-thematics, 167, 163-171. http://dx.doi.org/10.1016/j.dam.2013.11.021
- 26. Biggs, N. (1993) Algebraic Graph Theory. 2nd Edition, Cambridge University Press, Cambridge.
- 27. Bondy, J.A. and Murty, U.S.R. (1976) Graph Theory with Applications. Macmillan Press Ltd., London.
- 28. 师海忠, 常立婷, 赵媛, 张欣, 王海峰. 2r-正则图连通圈网络的Hamilton分解[J]. 计算机科学, 2016, 43(11A) (已录用).