Computer Science and Application
Vol.08 No.03(2018), Article ID:24217,9
pages
10.12677/CSA.2018.83035
Research on the Multi-Computing of Rational Security Based on Secret Sharing
Xinglan Zhang, Wei Zheng
Beijing University of Technology, Beijing
Received: Mar. 10th, 2018; accepted: Mar. 22nd, 2018; published: Mar. 28th, 2018

ABSTRACT
Through the analysis of the past, based on the analysis of rational-security multi-party computing protocol based on secret sharing, some of the problems are pointed out. In order to solve these problems, this paper redesigns a rational secure multi-party computing protocol based on secret sharing. In order to solve the problems exposed by the previous agreement, false points are mixed in real points and participants’ information about polynomial is masked during secret distribution.
Keywords:Secret Sharing, Secure Multi-Party Computation, Game Theory
基于秘密共享的理性安全多方计算的研究
张兴兰,郑炜
北京工业大学,北京
收稿日期:2018年3月10日;录用日期:2018年3月22日;发布日期:2018年3月28日

摘 要
通过对以往的基于秘密共享的理性安全多方计算协议的分析,指出了其中存在的一些问题,为了解决这些问题,本文重新设计了一种基于秘密共享的理性安全多方计算协议,通过在真实影子份额中随机的混入虚假影子份额,并且屏蔽掉参与者对于秘密分发阶段对于秘密多项式阶数等私密信息的了解,从而解决了之前协议所暴露出的问题。
关键词 :秘密共享,安全多方计算,博弈论

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
多方安全计算指在一个参与者都不信赖彼此的环境中,每位参与者都通过网络来共同完成各种计算任务的同时又不会泄露自己的数据 [1] 。这里面的安全是说我们既能够通过计算得到正确的结果,又不会让别的参与者得知我们输入的各种隐私信息。多方安全计算在我们的生活中随处可见,尤其是在现在这个互联网时代,比如在网上的拍卖会,网络上的投票系统 [2] 等等。
借助博弈论思想,我们可以实现在传统的协议中很难实现的公平性。文献 [3] 提出了一个思想,当人们无法预测何时得到计算结果时,他们会非常乐于去遵循协议。Naor [4] 等人为了使参与者严格的去遵守协议的约定,引入了博弈论的相关概念。但该方案设计比较复杂。在参考文献 [5] 中,Amjed设计了一个引入博弈论的方案,但是这个方案要求生成的多项式的幂次数之间的差值必须小于等于一,具有局限性。参考文献 [6] [7] 需要在我们使用的时候提供一些物理性的材料,比如信件等,不利于应用。在参考文献 [8] 中,同时考虑了善意的参与者和具有攻击性的参与者,在这个基础上,设计出了一种新的理性安全多方计算的方案。
现有的基于秘密共享的理性安全多方计算协议的基本思路均为屏蔽掉参与者对于多轮数据交互中“最后一轮”的认识,使参与者不知道协议到底在第几轮结束,因为如果参与者知道协议在第几轮结束,那么参与者完全可以在最后一轮中拒绝发送自己的影子份额,而会收到别的参与者的影子份额从而恢复出秘密,尽管别的参与者知道有参与者没有发出自己的影子份额,但是也已经晚了,因为那个参与者已经自己得到了秘密,因此根据反向递归原则,作为一个理性的参与者,他们从协议的第一轮开始就不会去执行这个协议。因此学者们提出了采用随机性策略的思想。将秘密重组过程重复很多轮,重复的次数是有限的但是参与者不知道协议要重复多少轮,其中,每一轮以一定概率是有意义的,只有在有意义的轮中才可以恢复出秘密,若在无意义的轮中背离,则协议将要终止,所有参与者都无法得到秘密。这一随机性,使得参与者由于无法判断当前轮是否能够得到秘密而不会去冒险背离,从而遵守协议,实现协议的公平性。
2. 背景知识
2.1. 传统的基于秘密共享多方安全计算模型
现有的基于秘密共享的多方安全计算模型一般是下面这种形式:
假设 是这样的一个函数:给定输入 ,计算 。接着利用 秘密共享机制在参与者之间分享结果S,即产生子份额 ,其中 可以通过某种运算计算出最终的结果S。然后分发者构造多个秘密多项式 ,使 。并产生多组影子份额队列 ,分别将这些影子子份额队列发送给对应的参与者 。参与者们通过不断的交换彼此的影子子份额恢复出彼此的秘密多项式从而获得秘密子份额,最终构造出计算结果S。
2.2. 可验证随机函数VRF
1999年Micali,Rabin等人提出可验证随机函数(verifiable random functions,VRF)的概念。随后几年关于可验证随机函数的工作主要有 [9] [10] [11] [12] 。
一个可验证随机函数包含多项式时间算法( )。它有如下四个性质:
1) Gen (函数参数生成单元)是概率算法,以1k为输入,输出 ,对于任意的 ,有 。
2) 对于由 生成的所有 ,不存在一个 使等式 成立,其中 。
3) 对于由
生成的所有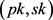 ,不存在一个
使等式
成立,其中
。
,不存在一个
使等式
成立,其中
。
4) 由 生成一组 ,将pk给恶意攻击者A。A主动去查询序列 ,对于每一个 都给予相对应的 。A输出一个序列 ,其中 。A随机生成一个bit位b去选择,如果 则A得到 ,否则A得到一个随机的y。最终A会
得到一个bit位 ,如果 则攻击成功。这个A成功的概率至多为 。
3. 已有的多方安全计算协议及分析
在背景知识部分我们已经了解到了基于秘密共享的安全多方计算协议的模型。目前已有的秘密多项式 设计方式一般有两种:一种是各个参与者 手中的秘密多项式 最高阶次数是相等的;另一种是参与者 手中的秘密多项式 最高阶次数的绝对值相差为1。本章将分别介绍这两种方式中存在的问题。
3.1. 秘密多项式最高阶次数相差为1的情况
Maleka S等人设计的协议的主要思想是将所有参与者被分配的秘密子份额再进一步划分为影子份额。下面给出主要的步骤 [13] :
1) 秘密分发阶段:分发者Dealer选取秘密 和秘密多项式
,
,然后通过某种计算方式将秘密S继续划分为子秘密
,例如
。Dealer生成两个秘密多项式
,满足
,两个秘密多项式
的阶数
相差为1。然后根据
生成不同的影子份额
并发送给参与者
;
和秘密多项式
,
,然后通过某种计算方式将秘密S继续划分为子秘密
,例如
。Dealer生成两个秘密多项式
,满足
,两个秘密多项式
的阶数
相差为1。然后根据
生成不同的影子份额
并发送给参与者
;
2) 秘密恢复阶段,参与者 以某种方式相互交换自己手中的影子份额。假设在第r轮交互中, 只有在收到对方的 后才继续执行协议;最后通过从别的参与者手中得到的影子份额恢复出对方的秘密多项式从而得到子秘密并计算出结果S。
3.2. 秘密多项式最高阶次数相同的情况
另一种是Feldman的思想 [14] ,他与3.1节中的不同之处就是构造的子秘密多项式的最高阶次数是相同的,其余步骤类似,就不在这里再次说明了。
3.3. 以往协议存在的问题
对于3.1节这种含密多项式 最高阶次数相差为1的思想来说,此处假设P1参与者的含密多项式的最高阶次数为3,则P1手中拥有3个影子份额,P2参与者的含密多项式最高阶的次数为4,P2手中拥有4个影子份额。假设在协议交互的第3轮中,P1将最后一个子份额发送给了P2,P2也将自己的第三个影子份额发送给了P1,那么协议顺利继续进行,会进入到第4轮,从P2的角度考虑,我们来分情况进行讨论,会出现如下3中情况:
当P2认为P1的子份额比自己少1个时。假如在这轮当中P2不发送自己的影子份额,而直接用前3轮获得的影子份额直接利用拉格朗日插值定理直接恢复出秘密S,那么最终结果就是P2一个人获得了秘密,而P1并不会获得秘密;
当P2认为P1的子份额和自己一样多。那么P2完全可以足够的等待至P1将他的子份额先发送过来,这样的情况下P2就可以独自恢复出秘密多项式 然后退出协议而P1并不会得到任何信息。即便P1不发送也没有什么关系,因为自己也没有发送将手中的最后一个子份额发送给P1,因此最后的结果最多是大家都没有恢复出要共享的秘密S,这也是一种纳什均衡,只是并不是大家希望所达到的纳什均衡;
当P2认为P1的子份额比自己多1个。此种情况下的P2更倾向于等待P1先把最后的影子份额发送给自己,因为此时P1已经可以利用从P2那里获得的影子份额恢复出秘密S,而且在自己还没有获得足够子份额的情况下将手中的所有子份额都给了对方,这样做也是具有隐患的,作为一个理性参与者是不倾向于这样做的。
对于3.2节的内容,我们可以知道因为P1和P2的秘密多项式的最高阶的次数是相等的,因此他们手中的影子份额数就是相等的,也就是说P1和P2彼此都知道对方手中握有的影子份额的数量。因为在安全多方计算中,参与者彼此暴露给其余参与者的数据越多越不好,参与者都想尽量少的暴露自己的各种信息去获得最终的运算结果,显然让其余参与者知道自己手中的影子份额数量就带来了一定的风险。
在秘密重组阶段,参与者集合中的各个参与者因为都知道最终的秘密份额总数,假如参与者总数为n,每个人都需要其余参与者的 个影子份额才能最终恢复出秘密S,大家在广播自己手中的影子份额的时候,其中一个参与者Pi拒绝放出自己的影子份额,而他却从广播中收到了其余参与者
的
个影子份额,那么参与者Pi最终会成为这个参与者集合中唯一一个能够恢复出秘密S的人,而其余参与者却什么都没有得到,因此通过逆向归纳法,具有这种隐患的安全协议,对于理性参与者来说也许大家从第一轮开始就不会去遵守这个协议,安全计算也就无法进行了。
个影子份额才能最终恢复出秘密S,大家在广播自己手中的影子份额的时候,其中一个参与者Pi拒绝放出自己的影子份额,而他却从广播中收到了其余参与者
的
个影子份额,那么参与者Pi最终会成为这个参与者集合中唯一一个能够恢复出秘密S的人,而其余参与者却什么都没有得到,因此通过逆向归纳法,具有这种隐患的安全协议,对于理性参与者来说也许大家从第一轮开始就不会去遵守这个协议,安全计算也就无法进行了。
从秘密分发的角度来说,由于秘密多项式的最高阶次数是固定的,而影子份额都是有效真实值,也就是说在秘密分发阶段只要截获到所有的影子份额那就一定能恢复出最终的秘密S而不需要与其余参与者交互,这就成为了一个隐患。
4. 一个全新设计的基于秘密共享的理性安全多方计算协议
假设要计算的函数为只有一个输出的函数,对于多个输出的可在此基础上扩展。协议中涉及的安全多方计算协议都是传统的基于不经意传输协议的,在基础知识部分介绍过其计算的过程,这里不再给出。
本文所设计的协议也是分为2个阶段 ,即秘密分发阶段和秘密重构阶段。我们假定参与者是2名,多名参与者同理也可以推出。
1) 秘密分发阶段
假设S为待共享的秘密( ), 。分发者参照分布概率为b的几何分布选择一个整数 为真实轮。M为总轮数, 。
分发者选择 、 、 和 函数,其中 、 和 、 ,都属于VRF。由 生成 ,由 生成 。
分发者选择一个多项式
,其中
,
,分发者计算
,这些点值为真实有效点值,可以凭借这些点值恢复出多项式
,然后分发者生成随机混淆函数
,这个函数可以是任意函数,因为不会影响到结果,因此x可以是任何数,最终形成由真实点值和虚假点值组合成的影子份额队列
,x可以为任意值。并且对影子份额队列做出承诺
。根据真实点值对在影子份额中的位置可以生成一个二进制串
,其中二进制位为1的位置为真实点值对在影子份额中的位置。分发者计算
及 。然后分发者将
、
、
。然后分发者将
、
、 、
、
、
及
发送给参与者PA。
、
、
、
及
发送给参与者PA。
分发者选择一个多项式 ,其中
,
,
,分发者计算
,这些点值为真实有效点值,可以凭借这些点值恢复出多项式
,然后分发者生成随机混淆函数
,其中
,
,
,分发者计算
,这些点值为真实有效点值,可以凭借这些点值恢复出多项式
,然后分发者生成随机混淆函数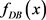 ,这个函数可以是任意函数,因为不会影响到结果,因此x可以是任何数,最终形成由真实点值和虚假点值组合成的影子份额队列
,x可以为任意值。并且对影子份额队列做出承诺
。根据真实点值对在影子份额中的位置可以生成一个二进制串
,其中二进制位为1的位置为真实点值对在影子份额中的位置。分发者计算
及
。然后分发者将
、
、
、
、
、
及
发送给参与者PB。
,这个函数可以是任意函数,因为不会影响到结果,因此x可以是任何数,最终形成由真实点值和虚假点值组合成的影子份额队列
,x可以为任意值。并且对影子份额队列做出承诺
。根据真实点值对在影子份额中的位置可以生成一个二进制串
,其中二进制位为1的位置为真实点值对在影子份额中的位置。分发者计算
及
。然后分发者将
、
、
、
、
、
及
发送给参与者PB。
2) 秘密重构阶段:在第r轮, ,PA、PB执行以下算法:
PB将 影子份额队列中的第r个影子份额 、 、 、 和 发送给PA。如果PA没有收到PB发送的信息或者PB发送的影子份额经过验证发现是错误的或者 或者 ,则PA输出 并且退出协议。如果 ,PA知道 为真是校验二进制位并且通知PB;否则 ,然后继续下一轮。
PA将 影子份额队列中的第r个影子份额 、 、 、 和 发送给PB。如果PB没有收到PA发送的信息或者PA发送的影子份额经过验证发现是错误的或者 或者 ,则PB输出 并且退出协议。如果 ,PB知道 为真是校验二进制位并且通知PA;否则 ,然后继续下一轮。
在PA、PB得知正确的校验位 、 之后,就能从影子份额队列 、 中找出真实有效的影子份额从而恢复出多项式 ,从而计算出 ,然后通过 计算出S从而获得安全多方计算的结果。
5. 协议分析
本节将从可行性、安全性以及效率这四个角度对协议进行分析。
5.1. 可行性分析
证明1 当各个理性参与者不知道协议真正的结束轮是在哪一轮时,彼此更倾向于将协议执行下去。
证明 通过反证法可知,要证明该问题其实就是要证明如果参与者知道协议在哪一轮结束,那么他们将没有合作执行协议的期望。如果参与者知道协议在哪一轮结束,那么在这一轮中恶意参与者可以通过发送虚假信息或者干脆不发送任何信息而独自获得秘密,因为这是协议的最后一轮,因此这些恶意参与者并不担心任何惩罚,所以作为理性的参与者,从逆向归纳法的角度来看,从协议的第一轮开始,所有参与者都将会保持沉默,他们将没有合作执行协议的期望,因此最终秘密并不会被重构出来。
证明完毕。
本章所设计的协议采用“随机最后一轮”的原则,使参与者并不知道到底哪一轮是最后一轮,因此根据证明1可知参与者将有共同合作执行协议的期望。
证明2 如果参与者按照协议要求执行协议,那么最终所有参与者都会获得秘密S。
证明 所有严格按照协议执行的参与者,在到达 轮时,参与者计算出 ,可知当前轮为 轮,因此在 轮也就是上一轮所得出的秘密是真实的校验位bit,由此可以从之前收到的影子份额队列中找到真实有效的影子份额,从而恢复出 ,然后求出要共享的子秘密,从而获得最后的安全多方计算的结果。
证明完毕。
证明3 在满足式 时,理性的参与者有动机遵守本章节所设计的协议。
证明 在执行协议时,参与者都是理性的,没有绝对的诚实参与者和恶意参与者,理性参与者只会根据所获得的效益来决定自己是否严格执行协议发送正确的影子份额。在本文协议中,参与者不能提前获知当前轮是不是真实轮。如果参与者想不遵守协议提前了解秘密,根据证明4可知他们只能通过猜测而获得,假如猜对秘密的概率为a,猜对者获得的收益为 ;则猜错的概率为 ,效益为 。所以猜测者的期望收益为 。
如果猜测者恰好在真实轮 进行攻击,概率为b,收益为 ;否则猜测者的效益为 .因此猜测者的期望收益最多为 。
参与者遵守协议获得的收益为U,为了让参与者能遵守协议,应该让 ,则参与者没有偏离协议的动机。
证明完毕。
5.2. 安全性分析
在秘密共享阶段,理性参与者的效用是根据能否得到秘密S来划分的。分4种情况来考虑:1、参与者Pi得到S, 都没有得到S时Pi的收益为t1;2、所有参与者都得到S为t2;3、任何参与者都没得到S为t3;4、Pi没得到S,而
得到了S的收益为t4。显然
。因此作为一个理性的参与者,他会根据这个顺序进行决策。
都没有得到S时Pi的收益为t1;2、所有参与者都得到S为t2;3、任何参与者都没得到S为t3;4、Pi没得到S,而
得到了S的收益为t4。显然
。因此作为一个理性的参与者,他会根据这个顺序进行决策。
证明4 作为理性参与者更愿意自己得到秘密而别的参与者不会得到秘密(独自得到秘密的收益为t1),则该理性参与者只能通过猜测确定S或者破解可验证随机函数(VRF)使伪造的影子份额不被检验出来。
证明:当参与者Pi严格遵守协议,每次都交互自己手中的影子份额时,参与者i希望能够独自恢复出密码S,则对于i来说在每轮共享影子份额的时候尽量靠后发送自己的影子份额,使自己能够比已经发送了影子份额的参与者早知道当前轮是否为最终轮。对于第j轮,若 ,因为没有到达结束轮,因此恢复出的校验位bit并不是真实的,因此得到的别的参与者发来的影子份额也就更加没有意义了。当 时,参与者仍然采取晚发送影子份额的方式,可以判断出已经到达真正的结束轮,上轮重构出的信息为真实信息。此时为了让自己独自获得秘密而别的参与者得不到秘密所以应该退出协议。同理,对于其他还没有来得及发送自己的影子份额的参与者也会直接退出方案而不发送自己手中的份额,此时对于已经发送了自己手中影子份额的人来说,秘密实际上已经无法成功恢复,但因为所有参与者都是理性的,为所有参与者的共识,故已发送影子份额的参与者分2中情况推断:
1) 如果已退出的参与者恢复出了结束信号,则可以推断出上一轮构造出的bit就是真实的校验位,因此这些已经发送了自己手中影子份额的人来说可以推出真实秘密S,然后退出秘密分享。
2) 如果已经退出的参与者并未恢复出结束信号,此时实际上所有参与者并没有恢复真实的校验位函数。所以此时已经退出的参与者如果想获得t1的收益,即独自获得这个秘密S,只能通过凭空猜测。
在多个参与者共同参与的协议中,如果参与者i选择发送伪造的影子份额,首先若其只选择给一部分人发送假的影子份额,给另一部分人发送真的影子份额,则对于收到的假的影子份额的人来说以后不会再跟他合作,这会在之后轮的交互中导致参与者i从别人那里获得的份额减少,有可能不满足门限值从而永远无法恢复出秘密S,如果他像所有都发送虚假影子份额,那就更不能恢复出秘密S了。
综上所述,可知参与者成功伪造影子份额的可能性微乎其微,相当于可验证随机函数被破解,这几乎是不可能的。可知理性参与者在本文协议中想获得t1的收益是不可能实现的,因此更趋向于按收益t2来做决策,即所有理性参与者都获得秘密S,该方案能够达到纳什均衡。
证明5 在我们的协议中,当总轮数M满足 时 会遵守协议,此时本文设计的协议能够达到纳什均衡。
证明 假设参与者猜测秘密S并猜对的概率为 ,因为是凭空猜测无任何依据,因此q几乎为无穷大,所以理性参与者更倾向于认为当前轮恢复的秘密为真实秘密,也就是猜出当前轮为真实轮,假设M为总轮数,则猜对的概率为
。
,因为是凭空猜测无任何依据,因此q几乎为无穷大,所以理性参与者更倾向于认为当前轮恢复的秘密为真实秘密,也就是猜出当前轮为真实轮,假设M为总轮数,则猜对的概率为
。
当参与者人数大于门限时。由题设可知:
所以可得
如果参与者i准备偏离协议进行推测,则把i恰好在猜测对当前轮为真实轮并退出协议的事件叫做C,把i未猜测对真实轮并退出协议的事件叫做D。则参与者i能获得的收益为
,其中 。
因此 。作为一个理性的参与者,当严格执行协议所获得的收益比违背协议所获得的收益大时,他就不会偏离协议。
证明完毕。
5.3. 协议效率分析
理性安全多方计算协议的实现仍然是基于随机性结束机制的,即将传统安全等多方计算协议的输出阶段扩展为多轮重组过程,每一轮都以概率b为真实轮,即在有意义轮中参与者能够恢复出真实的计算结果,但参与者并不知道哪一轮可以恢复出计算结果,因此从本文设计的协议来看,主要开销在于重构时的轮数M,轮数M服从参数为b的几何分布,所以方案的轮复杂度为 。
6. 总结
本文设计的安全多方计算方案从秘密分发阶段就将所有参与者的秘密多项式的阶数随机化,使各个参与者手中握有的真实有效的影子份额数量不一致,并在其中加入虚假无效的影子份额,只有交互进行到约定好的结束轮时才能获知校验位二进制从而知道真实有效影子份额所在的位置,即便在秘密分发阶段恶意参与者或黑客截获到所有影子份额也是没有意义的,因为他们并不知道哪些影子份额是真实的,有几个真实影子份额,这就加大了他们恢复出秘密S的难度。
基金项目
国家自然科学基金(10007016201201)。
文章引用
张兴兰,郑 炜. 基于秘密共享的理性安全多方计算的研究
Research on the Multi-Computing of Rational Security Based on Secret Sharing[J]. 计算机科学与应用, 2018, 08(03): 305-313. https://doi.org/10.12677/CSA.2018.83035
参考文献
- 1. Goldreich, O. (1998) Secure Multi-Party Computation. http://theory.lcs.mit.edu/
- 2. Cramer, R. (1999) Introduction to Secure Computation. In: Damgaard, I., Ed., Lectures on Data Security, Lecture Notes in Computer Science, Vol. 1561, 16-62. https://doi.org/10.1007/3-540-48969-X_2
- 3. Halpern, J. and Teague, V. (2004) Rational Secret Sharing and Multiparty Computation. Proceedings of the 36th Annual ACM Symposium on Theory of Computing (STOC 2004), 13-16 June 2004, Chicago, IL, 623-632. https://doi.org/10.1145/1007352.1007447
- 4. Kol, G. and Naor, M. (2008) Cryptography and Game Theory: Designing Protocols for Exchanging Information. Theory of Cryptography Conference (TCC 2008), 4948, 317-336. ttps://doi.org/10.1007/978-3-540-78524-8_18
- 5. Maleka, S., Amjed, S. and Rangan, C.P. (2008) The Deterministic Protocol for Rational Secret Sharing. Proceedings of the 22th IEEE International Symposium on Parallel and Distributed Processing, 14-18 April 2008, Miami, FL, 1-7. https://doi.org/10.1109/IPDPS.2008.4536558
- 6. Izmalkov, S., Micali, S. and Lepinski, M. (2005) Rational Secure Computation and Ideal Mechanism Design. Proceedings of the 46th Annual Symposium on Foundations of Computer Science (FOCS 2005), 23-25 October 2005, Pittsburgh, PA, 585-595. https://doi.org/10.1109/SFCS.2005.64
- 7. Fuchsbauer, G., Katz, J. and Naccache, D. (2010) Eficient Rational Secret Sharing in the Standard Communication Networks. Theory of Cryptography (TCC 2010), 5978, 419-436. https://doi.org/10.1007/978-3-642-11799-2_25
- 8. Asharov, G. and Lindell, Y. (2011) Utility Dependence in Correct and Fair Rational Secret Sharing. Journal of Cryptology, 24, 157-202. https://doi.org/10.1007/s00145-010-9064-z
- 9. Micali, S., Rabin, M.O. and Vadhan, S.P. (1999) Verifiable Random Functions. 40th Annual Symposium on Foundations of Computer Science (FOCS), 17-19 October 1999, New York City, NY, 120-130. https://doi.org/10.1109/SFFCS.1999.814584
- 10. Dodis, Y. (2003) Efficient Construction of (Distributed) Verifiable Random Functions. Public Key Cryptography—PKC 2003, 2567, 1-17. https://doi.org/10.1007/3-540-36288-6_1
- 11. Lysyanskaya, A. (2002) Unique Signatures and Verifiable Random Func-tions from the DH-DDH Separation. Advances in Cryptology|CRYPTO 2002, 2442, 597-612. https://doi.org/10.1007/3-540-45708-9_38
- 12. Dodis, Y. and Yampolskiy, A. (2005) A Verifiable Random Function with Short Proofs and Keys. Public Key Cryptography—PKC 2005, 3386, 416-431. https://doi.org/10.1007/978-3-540-30580-4_28
- 13. Maleka, S., Shareef, A. and Rangan, C.P. (2008) The Deterministic Protocol for Rational Secret Sharing. IEEE International Symposium on Parallel and Distributed Processing (IPDPS 2008), 14-18 April 2008, Miami, FL, 1-7. https://doi.org/10.1109/IPDPS.2008.4536558
- 14. Feldman, P. (1987) A Practical Scheme for Non-Interactive Verifia-ble Secret Sharing. 28th IEEE Symposium on Foundations of Computer Science (FOCS’87), 12-14 October 1987, Los Angeles, CA, 427-437. https://doi.org/10.1109/SFCS.1987.4