Computer Science and Application
Vol.08 No.04(2018), Article ID:24527,7
pages
10.12677/CSA.2018.84053
Reversible Medical Image Watermarking Based on Image Interpolation Error Expansion
Yue Chang, Xuan Wang
Shaanxi Normal University, Xi’an Shaanxi
Received: Apr. 3rd, 2018; accepted: Apr. 19th, 2018; published: Apr. 26th, 2018

ABSTRACT
Embedding watermark information into audio, image or video digital signals can protect the copyright information of products. After the watermark information is extracted, the original image can be restored without any distortion in the reversible watermark image. In this paper, we use the additive interpolation error extension method to embed watermark data into the smooth region of the image. Unlike previous watermarking methods, the additive interpolation error expansion embeds bits “1” or “0” by adding or expanding the interpolation error additively. Since only slight modifications have been made to the pixels of the smooth area, the high quality of the image is preserved. The experiment results show that the proposed scheme can provide greater payload capacity and higher image fidelity, compared with other most advanced schemes.
Keywords:Medical Image, Interpolation Image, Additive Interpolation Error Expansion, Reversible Watermark
基于图像插值误差扩展的可逆医学图像水印
苌悦,王晅
陕西师范大学,陕西 西安
收稿日期:2018年4月3日;录用日期:2018年4月19日;发布日期:2018年4月26日

摘 要
将水印信息嵌入到音频,图像或视频等数字信号中可以保护产品的版权信息。在提取水印信息后,可逆水印图像可以在没有任何失真的情况下恢复原始图像。在本文中,我们利用加法插值误差扩展技术水印数据嵌入到图像的平滑区域中。与以前的水印方法不同,加法插值误差扩展通过对插值误差相加扩展或保持不变来嵌入比特“1”或“0”。由于只对平滑区域的像素进行了轻微的修改,因此保留了图像的高质量。实验结果还表明,与其他最先进的方案相比,所提出的方案可以提供更大的有效载荷容量和更高的图像保真度。
关键词 :医学图像,插值图像,加法插值误差扩展,可逆水印

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着区域医疗和远程诊断技术的飞速发展,越来越多的医学图像开始在公网上进行传输。由于公网固有的安全隐患,医学图像数据的安全性受到巨大挑战 [1] 。数字水印技术很好地解决了这一问题,它通过将一段具有特定含义的标识信息嵌入在载体医学图像中,能实现医学图像的真实性和完整性认证、电子病历EPR (Electronic Patient Record)的隐藏和版权保护 [2] [3] [4] 。然而,通常的有损数字水印算法并不能满足医学对象的应用需求,因为作为诊断依据的医学图像对完整性有着严格的限制,要求含水印的医学图像在水印提取出来后,必须能恢复到原始的状态,即无损数字水印技术。目前,无损数字水印技术已经广泛应用在对完整性敏感的工程图设计、医学信息和法律证据等领域。
图像数据隐藏共分为两类,分别为可逆和不可逆的,而且无论是哪一类,水印嵌入都会改变载体,而且水印信息嵌入的越多,就会导致失真性越大,也就意味着数据隐藏性越差.所以,越来越多的专家和学者开始研究如何在确保低失真的基础上,把尽可能大的容量嵌入进去.可逆水印的特点是在提取水印信息后可以完全无损地恢复原始图像,主要应用于对图像质量要求极高的领域,如医学影像,遥感地图和法律证据图像等。医学图像具有与自然图像不同的特点,主要表现在图像精度要求高,相对平滑以及有大量空白区域(无信息的黑色区域)。MB Andra等在混合预测的基础上通过扩展预测误差来提高可逆水印算法的容量 [5] ;MP Turuk等基于小波变换的方法利用量化函数来嵌入多个水印 [6] ;陈亮等利用图像小波变换后的高频子带系数进行水印嵌入,改进传统的直方图平移方法,设计了嵌入参数选择算法 [7] 。本文基于图像插值设计研究了可逆水印算法,介绍了可逆信息隐藏技术的研究现状、特性、评价标准以及研究前景,讨论了常见的插值算法,提出了本文所用的插值算法;在研究插值图像可逆原理的基础上,探讨了水印的嵌入、提取以及载体还原技术。
2. 加法插值误差扩展
首先通过公式(1)获得插值误差
(1)
其中 是像素值为X的插值。LM和RM表示插值误差直方图中的两个最高点,假设 ,我们可以把插值误差分为两部分:
左侧插值误差(LM):插值误差e满足
右侧插值误差(RM):插值误差e满足
加法插值误差扩展的公式为:
(2)
其中 是扩展后的插值误差,b是嵌入的水印位,其中sign(.)函数定义为
(3)
其中参数LN与RN定义为
(4)
扩展之后得到水印像素
(5)
在提取过程中,使用相同的插值算法,我们可以获得相同的插值 ,并得到相应的插值误差
(6)
在已知LM,LN,RM,RN的情况下,即可提取嵌入的水印位
(7)
然后应用加法插值误差扩展的逆函数来恢复原始插值误差
(8)
最终我们可以恢复原始像素
(9)
3. 插值算法
在现有的研究中,使用的放大图像的方法均为不可逆的,就算把同一幅图像放大之后再按同样的比例缩小,在图像处理过程中也会有损失产生 [8] 。假设低分辨率图像 是由高分辨率图像 通过 直接下采样得到的。如图1所示,黑点代表下采样像素xl,白点表示遗失的像素。用所选插值方法放大的图像,由大小为m ´ n的图像得到2m ´ 2n的图像。
插值的关键问题是如何推断和利用缺失像素与相邻像素之间的相关性。首先,那些遗失的像素
在由四个低分辨率像素围绕的中心位置处被内插。其次,其他缺失的像素
和
在已经恢复的像素的帮助下进行插值预测。如图1(b)所示,我们可以沿着45°和135°两个方向对 进行插值预测。预测过程如下:
进行插值预测。预测过程如下:
计算 和 两个方向插值结果
(10)

Figure 1. (a) Formation of a low-resolution image from the high-resolution image; (b), (c) interpolation of residual samples of high-resolution; (d) the interpolation of the original pixels
图1. (a) 从高分辨率图像形成低分辨率图像;(b),(c) 高分辨率插值图像的剩余样本;(d) 原始像素的插值
计算两个方向的插值误差 和
(11)
选择一个最佳的权重对来使 成为X的一个很好的估计, 需满足如下要求
(12)
确定权重w45和w135以最小化 的均方误差
(13)
其中 和 分别是 和 的方差。
为了平衡计算的复杂性和像素的一致性,计算u
(14)
5) 计算 和
(15)
其中
由式(10)~(15)即可得到 。
在估计缺失的高分辨率像素 之后,可以类似地估计剩余像素 和 。参照图1(c),黑点表示低分辨率像素,灰点表示第一步中的估计像素,白点表示要内插的像素。如图2(c)中,除了将两个方向修改为0˚和90˚之外,其余部分的计算方法与第一步中描述的类似。最后,通过上述过程重建整个高分辨率图。
4. 水印的嵌入与提取
医学图像与一般的图像有一定的区别,不仅仅是图像精度要求高,而且还有相对平滑以及有大量空白区域(无信息的黑色区域),我们选择在图像的平滑区域嵌入水印,保留图像变化较大的区域,可以在保证图像嵌入率的前提下不影响图像质量。
嵌入流程:
设原图像为I,待嵌入的水印为
Step1:对图像进行边缘提取,得到二值图像,将图像分为16 × 16大小的块,计算二值图像每块的和sum,设立阈值T = 20,对sum < T的图像标记为block并进行嵌入,其余块保持不变。建立二值图像,并对将要进行嵌入的块map的位置标记为1;
Step2:利用式(10)~(15)对块block进行上述的插值图像预测,并求出每个像素的插值误差e;
Step3:对插值误差e利用公式进行扩展,并嵌入水印,得到扩展后的误差 ;
Step4:利用式(1)~(5)嵌入水印后的像素,即完成了水印的嵌入;
Step5:对于嵌入水印后像素发生溢出的位置,建立位置图,发生溢出的位置直接跳过并且在位置图中标记为1,不发生溢出的位置标记为0。
用流程图可表示为图2所示。
水印的提取过程与嵌入流程相反,过程如下:
Step1:将图像分为16 × 16大小的块,获取嵌入时用到的每个块的LM,LN,RM,RN;
Step2:对标记为map = 1的块利用式(6)~(8)进行提取,对位置图标记为1的位置跳过,即可得到误差e和嵌入的水印位b;
Step3:利用式(9)恢复图像的原始像素X。
5. 实验结果
本次实验的原始图像采用512 × 512大小的医学图像,如图3所示的三张图像,嵌入的水印为随机二进制位。为了对实验结果进行分析比对,采用峰值信噪比(PSNR)和嵌入容量(嵌入到载体图像的比特位的个数,用bits表示)作为算法的性能评估标准。
为了分析比较,将本方案和文献 [5] [6] [7] 进行比对,结果如表1所示。从表1可以看出,相较于其他3种方法,本文方法不管在嵌入容量还是峰值信噪比(PSNR)上都有明显的提高。
图4给出了不同的载体图像在不同的嵌入容量下的 PSNR值测试结果。
6. 结论
本文提出了一种新的可逆水印方案。与使用预测或小波技术的最新方案不同,所提出的方案使用插值技术来产生误差,相邻像素之间具有更大的去相关能力。通过对这些插值误差应用加法扩展,我们实

Figure 2. Flowchart of embedding
图2. 嵌入流程图
 (a)
(a)  (b)
(b) 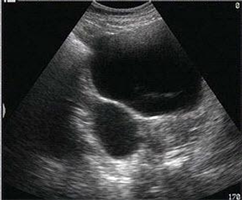 (c)
(c)
Figure 3. Original image (a) CT image; (b) MRI image; (c) Ultrasound image
图3. 原始图像 (a) CT图像;(b) MRI图像;(c) 超声图像

Figure 4. PSNR test results for different carrier images with different embedding capacities
图4. 不同载体图像在不同的嵌入容量下的PSNR测试结果
Table 1. Comparison in three images of capacity and PSNR
表1. 三种图像容量和PSNR的对比
现了高效的可逆水印方案,该方案在不牺牲嵌入容量的情况下保证了高质量的图像质量。根据实验结果,所提出的可逆方案提供了更高的容量并且为水印图像实现了更好的图像质量。另外,所提出的方案的计算成本很小。
文章引用
苌 悦,王 晅. 基于图像插值误差扩展的可逆医学图像水印
Reversible Medical Image Watermarking Based on Image Interpolation Error Expansion[J]. 计算机科学与应用, 2018, 08(04): 480-486. https://doi.org/10.12677/CSA.2018.84053
参考文献
- 1. Hu, J.K., Chen, H.H. and Hou, T.W. (2010) A Hybrid Public Key Infrastructure Solution (HPKI) for HIPAA Privacy/Security Regula-tions. Computer Standards & Interfaces, 32, 274-280. https://doi.org/10.1016/j.csi.2009.04.005
- 2. Tan, C.K., Ng, J.C., Xu, X.T., et al. (2011) Security Protection of DICOM Medical Images Using Dual-Layer Reversible Watermarking with Tamper Detection Capability. Journal of Digital Imaging, 24, 528-540. https://doi.org/10.1007/s10278-010-9295-4
- 3. Deng, X.H., Chen, Z.G., Deng, X.H., et al. (2011) A Novel Dual-Layer Re-versible Watermarking for Medical Image Authentication and EPR Hiding. Advanced Science Letters, 4, 3678-3684. https://doi.org/10.1166/asl.2011.1886
- 4. Nayak, J., Bhat, P.S., Acharya, U.R., et al. (2009) Efficient Storage and Transmission of Digital Fundus Images with Patient Information Using Reversible Watermarking Technique and Error Control Codes. Journal of Medical Systems, 33, 163-171. https://doi.org/10.1007/s10916-008-9176-2
- 5. Vinoth, K.C. and Natarajan, V. (2016) Hybrid Local Prediction Error-Based Difference Expansion Reversible Watermarking for Medical Images. Computers & Electrical Engineering, 53, 333-345. https://doi.org/10.1016/j.compeleceng.2015.11.033
- 6. Turuk, M.P. and Dhande, A.P. (2016) A Novel Reversible Multiple Medical Image Watermarking for Health Information System. Plenum Press, New York, NY.
- 7. 陈亮, 刘惠文, 邓小鸿. 基于整数小波变换的数字图像可逆水印算法[J]. 计算机应用与软件, 2016, 33(4): 286-291.
- 8. Luo, L., Chen, Z., Chen, M., et al. (2010) Reversible Image Watermarking Using Interpolation Technique. IEEE Transactions on Information Forensics & Security, 5, 187-193. https://doi.org/10.1109/TIFS.2009.2035975
