Computer Science and Application
Vol.
09
No.
03
(
2019
), Article ID:
29221
,
14
pages
10.12677/CSA.2019.93063
The Data Collection Scheme for Sparse Signals in Large-Scale Wireless Sensor Networks
Ruiqing Li, Hui Wang
Zhejiang Normal University, Jinhua Zhejiang

Received: Feb. 22nd, 2019; accepted: Mar. 6th, 2019; published: Mar. 13th, 2019

ABSTRACT
In a successfully deployed wireless sensor network, the sensing data taken directly from the sensor nodes are subject to a large amount of redundancy due to their temporal and spatial correlations. Therefore, we need to design an effective data collection scheme. Compressive sensing is a popular data collection technology. It includes three core topics: sparse representation of signals, design of observation matrix, and signal reconstruction. This paper focuses on the sparsity of signals. Firstly, the sparsity performance is analyzed from two aspects: real signals and synthetic signals. In compressive sensing, different orthogonal transforms make the signal different levels of sparsity. In order to study the sparsity of the signal further, we have designed two orthogonal transforms, namely Row-trans transform and Col-trans transform. It is found through experiments that the sparse performance of Fourier transform, discrete cosine transform and wavelet transform is relatively poor. The sparse performance of Row-trans transform and the Col-trans transform is better. As far as the reconstruction error is concerned, in the 1800 experimental measurements, the reconstruction errors of the signal under the Row-trans transform and the Col-trans transform are relatively stable, and the error rate are low, which is obviously superior to other orthogonal transforms. The reconstructed signal is closer to the original signal.
Keywords:Wireless Sensor Network, Compressive Sensing, Sparsity, Orthogonal Transforms, Reconstruction Error
大规模无线传感器网络中稀疏信号的数据收集策略
李瑞晴,王晖
浙江师范大学,浙江 金华

收稿日期:2019年2月22日;录用日期:2019年3月6日;发布日期:2019年3月13日

摘 要
在成功部署的无线传感器网络中,从传感器节点采集的感知数据由于时间和空间相关性会存在大量冗余,所以我们需要设计有效的数据收集方案。其中,压缩感知是常用的一种数据收集技术,它包括了三个核心技术:信号的稀疏表征、观测矩阵的设计、信号重构。本文主要对信号的稀疏性进行了研究。首先,从真实信号和合成信号两个方面对其稀疏性进行了分析。在压缩感知中,不同的正交变换使得信号的稀疏性不同。其次,为了更好地研究信号的稀疏性,我们设计了两种正交变换,即Row-trans变换以及Col-trans变换。通过实验发现,傅里叶变换、离散余弦变换、小波变换的稀疏性能比较差,而Row-trans变换、Col-trans变换的稀疏性更好。就重构误差而言,在1800次实验测量中,信号在Row-trans变换、Col-trans变换下重构误差比较稳定,误差值较小,明显优于其他几种正交变换,得到的重构信号更接近于原始信号。
关键词 :无线传感器网络,压缩感知,稀疏性,正交变换,重构误差

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在无线传感器网络 [1] 中,我们通过部署传感器节点,利用感知识别技术,让物品“开口说话,发布消息”,从而产生大量感知数据。这些感知数据反映了物理世界特定条件下的某种真实状态,因而蕴涵了大量直接的或潜在的有价值信息。但是,由于传感器节点部署在一定的监测区域内,采集到的感知数据存在一定的时间和空间相关性,故将采集到的原始数据不经处理直接传送到汇点的这种方式效率是非常低下的。因此,如何设计有效的数据收集策略成为学者极为关注的一个技术难题。
传感器网络一般由成千上万个传感器节点组成,越接近汇点的节点需要承担越重的中继通信任务,导致越接近汇点的节点功率消耗越快,形成难以避免的网络热点问题。该问题严重影响了整个无线传感器网络的生命周期,设计一种有效的数据收集策略,提高网络生命周期成为亟需解决的关键性难题。
在数据收集方案中,压缩感知 [2] - [7] (Compressive sensing)是一种新兴技术。通过利用信号的稀疏特性,用随机采样获取信号的离散样本,然后通过非线性重建算法完美地重建信号。压缩感知理论指出,只要信号是可压缩的或在某个变换域上可以被稀疏表征 [8] 的,那么就可以用一个优化问题从这些少量的投影中以高概率重构出原信号,这样的投影包含了重构信号的足够信息。
我们采用文献 [9] 所说的网络拓扑,即假设将一个具有N个节点和1个汇点的传感器网络部署在一个边长为L的方形区域内。我们将汇点部署在监测区域的中心位置。并将监测区域均分为具有n个相同面积的单元格的网格,我们要求每一个单元格只能放置一个节点,这个节点可以放置在单元格的任意一个位置,节点只能与小于或等于r(n)的范围内并且向着汇点方向的邻节点进行通信。汇点位于部署的监测区域的中心位置。
本文以压缩感知技术为主要技术框架对信号的稀疏性进行研究。首先,我们分别采集物理世界中八种不同场景的真实信号,并且设计了人工合成信号。其次,列举了几种经典的正交变换,分别为离散傅里叶变换、离散余弦变换、小波变换。为了更好地研究信号的稀疏性,我们设计了两种正交变换,分别为Row-trans变换以及Col-trans变换。并将这五种正交变换在压缩感知技术上加以实现。通过实验,对比其性能,我们发现傅里叶变换和离散余弦变换下信号的稀疏性不太好,小波变换稀疏性居中,而Row-trans变换以及Col-trans变换稀疏性能最好并且它们的重构误差数值小且比较稳定。
文章构成如下:第二节,介绍几个与压缩感知相关的知识点,包括有限等距性质,可压缩性数据,随机矩阵,稀疏随机投影;第三节,介绍了本文的主要技术——压缩感知技术的数据和网络模型以及技术框架;第四节,设计了人工合成信号,并且采集真实信号,通过五种正交变换,包括:傅里叶变换、离散余弦变换、小波变换以及Row-trans变换以及Col-trans变换对采集到的信号进行稀疏化;第五节,通过实验将不同的正交变换矩阵应用于压缩感知技术,对比其性能;第六节,文章的结论以及未来的工作。
2. 相关知识
在本文的数据收集方案中,我们将会涉及到以下几个相关知识:有限等距性质 [2] [10] [11] [12] (Restricted Isometry Property,以下简称RIP),可压缩性数据,随机矩阵,稀疏随机投影。
2.1. RIP性质
如果一个信号的大部分分量都为零,那么这个信号被称为稀疏信号 [2] [7] 。有限等距性质是完全重构稀疏信号的充分条件,对于稳定性的分析非常有效,它实际上是针对观测矩阵 的约束。其定义如下:
定义1:对于所有的s-稀疏向量
,矩阵
的第s个有限等距常数 [2]  ,
,使得下述公式成立:
,
,使得下述公式成立:
(2-1)
则矩阵 满足有限等距性质。其中 为有限等距常数,是指满足RIP的最小 ,如下定义:
(2-2)
这里的 是正交变换矩阵。
RIP性质保证了观测矩阵不会把两个不同的K稀疏信号映射到同一个集合中,即保证原空间到稀疏空间的一一映射关系,它要求从观测矩阵中抽取的每M个列向量构成的矩阵是非奇异的,满足RIP的关键是如何确定非零系数的位置来构造出一个可解的M × K线性方程组。
2.2. 可压缩性数据
根据观察,许多现实世界的信号是可压缩的,例如具有有界导数和有界变化信号的平滑信号,在某些变换域中是可压缩的 [13] [14] 。因为它们通过稀疏信号在适当的变换域中能够得到很好的近似,在总信号能量没有太大损失的情况下保留变换系数较大的k项,舍弃剩余的较小的变换系数。如果变换系数的大小像幂率一样成衰减模式,则数据是可压缩的。
将收集到的数据向量 ,以及正交变换矩阵 ,通过傅里叶变换或者小波变换得到变换系数 ,按从大到小的顺序对变换系数进行排列,有
,则第i个变换系数满足
(2-3)
其中R是一个常数,p控制变换系数的可压缩性,P越小,衰减速率越快。
2.3. 随机投影
随机投影 [13] [15] 可以保证恢复可压缩数据的近似最优逼近,并且误差非常小,只需要 数据的随机投影就可以产生与使用k个最大变换系数的最佳近似误差相当的误差近似值。考虑包含独立同分布项的随机投影矩阵
(2-4)
k个随机投影 可以产生数据x的近似值 ,误差为
其中 为与P相关的函数。
2.4. 稀疏随机投影
压缩感知的一个关键结果是,随机选择M × N维高斯矩阵(其中各项由遵循标准正态分布的独立随机变量组成),或伯努利矩阵(其中各项是独立的随机变量,取值+1和−1的概率相等)。对于 中的数据,我们希望找到最少数量的稀疏随机投影 [13] [14] [16] [17] 来恢复近似值,其误差与最佳k项近似值相当。我们考虑一个M × N稀疏随机矩阵,其中项非零的概率为1/s,因此平均每行有N/s个非零值,则稀疏随机投影矩阵 ,M × N,构成如下:
(2-5)
其中参数s表示随机投影的稀疏度。因此,如果1/s = 1,则随机矩阵不具有稀疏性;并且如果 ,则随机矩阵的每一行中期望的非零数为logN。
3. 压缩感知
压缩感知 [2] - [7] (Compressive sensing)也称压缩采样或稀疏采样,利用信号在某个变换域的稀疏特性,用随机采样获取信号的离散样本,通过非线性重建算法重建信号。压缩感知理论指出,只要信号是可压缩的或在某个变换域是稀疏的,就可以用一个优化问题从这些少量的投影中以高概率重构出原信号。其新颖之处在于采样速率不决定于信号的带宽,而决定于信息在信号中的结构和内容。
3.1. 压缩感知框架
压缩感知包括三个核心问题:信号稀疏变换、观测矩阵设计、重构算法,如下图1所示。
其中,信号x是长度为N的一维离散信号,可以看成是N×1维的列向量, 。自然
界中大多数信号都具有稀疏性,只要找到合适的变换基就可以使原始信号变为稀疏信号。假设信号x是正交基 下的稀疏信号,即,
其稀疏度为s。如果能找到一组与
不相关的M × N维的观测基
,用其观测信号得到一个长度为M的一维观测信号y(
),即,
那么就可以通过求解
最小化问题,从观测值y中以极高的概率来恢复原始信号。
是随机采样的过程。压缩感知的目标是利用信号的稀疏性或可压缩性,压缩感知可压缩的信号。
下的稀疏信号,即,
其稀疏度为s。如果能找到一组与
不相关的M × N维的观测基
,用其观测信号得到一个长度为M的一维观测信号y(
),即,
那么就可以通过求解
最小化问题,从观测值y中以极高的概率来恢复原始信号。
是随机采样的过程。压缩感知的目标是利用信号的稀疏性或可压缩性,压缩感知可压缩的信号。
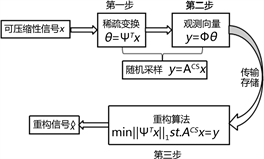
Figure 1. Compression sensing framework
图1. 压缩感知框架
3.2. 压缩感知数学模型
3.2.1. 稀疏信号的表示
设有可压缩性信号 ,它在某个正交变换 上是稀疏的,这里的正交变换可以用傅里叶变换或者小波变换 [18] 来表示,则有以下公式成立:
(3-1)
其中
是信号x在正交变换上的投影系数,x与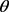 是同一个信号的等价表示,若
中有k非零系数或者k个远大于其他系数的值,则称信号x在正交变换
上是k-稀疏信号,即,信号x的稀疏度为k。信号稀疏表示的目的就是在给定的超完备字典中用尽可能少的原子来表示信号,从而使我们更容易地重建信号,更方便进一步对信号进行加工处理。
是同一个信号的等价表示,若
中有k非零系数或者k个远大于其他系数的值,则称信号x在正交变换
上是k-稀疏信号,即,信号x的稀疏度为k。信号稀疏表示的目的就是在给定的超完备字典中用尽可能少的原子来表示信号,从而使我们更容易地重建信号,更方便进一步对信号进行加工处理。
3.2.2. 观测向量
设计一个与上述正交变换矩阵不相关的观测矩阵 对稀疏系数进行观测得到观测集合
(3-2)
这里的观测矩阵
可以采取随机高斯矩阵、随机伯努利矩阵等一些随机测量矩阵。此过程也可以解释为信号x通过传感矩阵
进行非自适应观测,即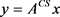 。这一过程的目的是通过上式找到最稀疏的解
,从而更好地恢复原始信号x。
。这一过程的目的是通过上式找到最稀疏的解
,从而更好地恢复原始信号x。
3.2.3. 重构信号
信号重构是压缩感知的最后一步,由于观测数量M远小于信号长度N,故重构问题是一个解欠定性方程组 [19] 的优化问题。当原始信号 是稀疏的或可压缩时,求解欠定方程组可转化为最小化 问题:
(3-3)
但求解最小化 问题是一个NP-hard问题,它需要列举信号中非零值的所有排列可能方式,无法直接求解,故我们可以通过求解凸优化 [20] 问题来代替最小化 问题,即当观测矩阵 满足RIP性质时,最小化 问题可以转化为数值上容易处理的最小化 问题:
(3-4)
我们可以通过上式的优化方式获得最稀疏的系数 ,从而获得重构信号 :
(3-5)
4. 收集信号与正交变换
我们在特定变换下合成稀疏信号,这些合成信号,可以精确控制自身的稀疏程度,当构造的信号足够稀疏时,与普通路由方案相比,压缩感知取得了实质性的收益。然而,真正的信号问题是找到一个很好的转换,在某一特定域中对它们进行稀疏处理,我们对比了几种不同的正交变换,并将其用于压缩感知。
4.1. 收集信号
信号收集包括两部分内容:真实信号和人工合成信号。从自然界中收集到的信号大都可以进行稀疏表示,但是我们很难收集到特定信号,所以设计了人工合成信号对压缩感知性能进行了研究。
4.1.1. 真实信号
我们还采集了来自不同环境现象的真实信号。我们在自然环境中随机部署具有100个Zigbee节点的Zigbee网络,包括温湿度传感器、空气质量传感器、光敏传感器,用于采集真实信号。Zigbee是一种无线自组织网络通信技术,由Zigbee联盟制定。它是基于IEEE 802.15.4标准下的低功耗局域网协议,其特点为近距离、高容量、低成本、低速率、低功耗,主要用于距离短、功耗低且传输速率不高的各种电子设备之间,进行数据传输。它可以工作在2.4 GHz (全球流行)、868 MHz (欧洲流行)和915 MHz (美国流行) 3个频段上,分别具有最高250 kbit/s、20 kbit/s和40 kbit/s的传输速率,其传输距离在10 m~75 m的范围内。
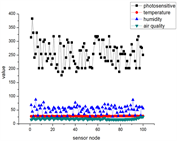
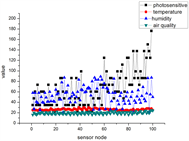
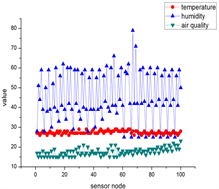
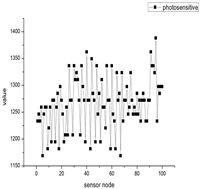
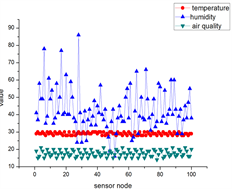
真实物联网信号 构成如下(图2):
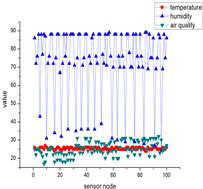
表示100个温度传感器节点采集到的数据, 表示第i个节点采集到的数据。
表示100个湿度传感器节点采集到的物联网数据, 表示第i个节点采集到的数据。
表示100个空气质量传感器节点采集到的物联网数据, 表示第i个节点采集到的数据。
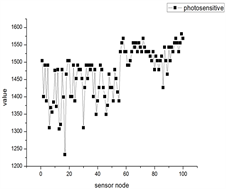
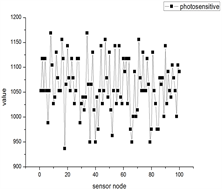
表示100个光敏传感器节点采集到的物联网数据, 表示第i个节点采集到的数据。
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
 (e1)
(e1)
 (e2)
(e2)
 (f1)
(f1)
 (f2)
(f2)
 (g1)
(g1)
 (g2)
(g2)
 (h1)
(h1)
 (h2)
(h2)
Figure 2. Sampling signals of different scenes, each sampling number includes 4 kinds of data, namely temperature, humidity, air quality, photosensitive
图2. 不同场景的采样信号,每一个采样号包括4种数据,分别为温度、湿度、空气质量、光敏
4.1.2. 人工合成信号
在自然间中很难采集到特定的信号,所以我们需要设计人工合成信号来对压缩感知的性能进行研究。在自然间中很难采集到特定的信号,所以我们需要设计人工合成信号来对压缩感知的性能进行研究。我们将信号x用矩阵的形式表示,通过构建频域中的二维离散信号x来构建的信号 [7] 矩阵。信号x的构建如下:
第一步:定义K,令 ,其中N是二维信号中数值的总量。构建初始信号 ,它的项记为 , ,则有
(4-1)
其中 数值可以在区间 内随机选取,又因为信号往往会存在一些噪声信号,因此引入常数 。
第二步:定义一个二维的频率掩模函数 ,在位置 的取值分下面两种情况,当 或者 时为1,当 时为0。函数定义如下:
(4-2)
第三步:通过 和 做乘积来获得信号 ,它的项 构成如下:
(4-3)
4.2. 几种经典的正交变换
在压缩感知中信号必须在某种变换下可以稀疏表示,信号的稀疏表示就是将信号投影到正交变换基,其大部分变换系数的绝对值很小或者为零,所得到的变换向量是稀疏的。下面介绍几种经典的正交变换。
4.2.1. 离散傅里叶变换
离散傅里叶变换(Discrete Fourier Transform,缩写为DFT),是傅里叶变换在时域和频域上都呈离散的形式,将信号的时域采样变换为其离散时间傅里叶变换的频域采样。
对于N点序列 ,它的离散傅里叶变换为:
(4-4)
其中e是自然对数底数,i是虚数单位。将上述变换写成矩阵形式:
即 ,其中 为变换矩阵,将变换矩阵 乘以一个系数 使其变为正交矩阵可得离散傅里叶变换基(矩阵):
(4-5)
4.2.2. 离散余弦变换
离散余弦变换(DCT)是与傅里叶变换相关的另一种变换,它类似于离散傅里叶变换(DFT),但是只使用实部,不需要考虑虚部。离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换,这个离散傅里叶变换是对一个实偶函数进行的。大多数的自然信号的能量都集中在离散余弦变换后的低频部分,而且当信号具有接近马尔可夫过程的统计特性时,离散余弦变换的效果能够接近理论上的最佳变换——Kahunen-Loeve变换(K-L变换)。
离散余弦变换是一种线性的可逆函数 (R表示实数的集合),或者等价于一个 {\displaystyle n\times n}的方阵,根据下列公式,把N个实数 变换到另外N个实数 :
(4-6)
给上式中的
和
分别乘以
,相应的给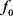 和
乘以
,则可以将上述变换转化为正交矩阵:
和
乘以
,则可以将上述变换转化为正交矩阵:
(4-7)
4.2.3. 小波变换
小波变换(wavelet transform,WT)继承和发展了短时傅立叶变换(STFT)局部化的思想,STFT是给信号加窗,分段做FFT;而小波变换并没有采用窗的思想,更没有做傅里叶变换,它直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基,提供了一个随频率改变的“时间-频率”窗口,通过变换能够充分突出问题某些方面的特征,能对时间频率的局部化分析,通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节。
设 是平方可积函数 , 是基本小波或母小波函数,则小波变换公式如下:
(4-8)
其中,尺度因子a控制小波函数的伸缩,对应于频率(成反比),平移因子 控制小波函数的平移,对应于时间。设有母小波 ,记 ,其中j,k为任意的整数。如果函数族
构成空间 的标准正交基,则称 是正交小波。Haar函数是小波分析中最早用到的一个具有紧支撑的正交小波函数,也是最简单的一个小波函数,它是支撑域在 范围内的单个矩形波,其母小波为
(4-9)
其对应的缩放方程式为:
(4-10)
4.3. 设计正交变换
在压缩感知中,已有的变换并不能达到我们对信号稀疏性的要求,因此我们设计了如下的正交变换。
4.3.1. Row-trans变换
第一步:将采集到的信号写成矩阵的形式,合成信号可以省略此步骤,对于真实信号 ,作如下变换,得到矩阵 ,其中 :
 (4-11)
(4-11)
第二步:将 中的项成对相减取其绝对值,构成矩阵 ,其中的项记为 :
(4-12)
第三步:给 中的每一项均乘以其倒数得到 :
(4-13)
第四步:给 做Householder变换,得到变换矩阵 ;
第五步:构造变换矩阵 :
(4-14)
其中I表示单位矩阵。
证明:因为 是Householder变换,故满足正交性,即 ,其中E是单位矩阵,故
故此得证矩阵 是正交变换。
4.3.2. Col-trans变换
第一步:将采集到的信号写成矩阵的形式,合成信号可以省略此步骤,对于真实信号 ,作如下变换,得到矩阵 ,其中 :
(4-15)
第二步:将 中的项成对相减取其绝对值,构成矩阵 ,其中的项记为 :
(4-16)
第三步:给 中的每一项均乘以其倒数得到 :
(4-17)
第四步:给 做Householder变换,得到变换矩阵 ;
第五步:构造变换矩阵 :
(4-18)
其中I表示单位矩阵。
5. 实验
我们在压缩感知基础上对信号进行处理,获得重构信号 ,并对原始信号x与重构信号 之间的重构误差进行讨论。重构误差定义如下:
(5-1)
5.1. 搭建实验平台
本次实验使用数据模拟器产生的合成信号以及自己收集的真实信号,在100*100 m的监测区域内随机部署传感器节点以及1个位于中心位置的汇点。汇点接收到来自传感器节点的读数并对其进行压缩感知再对数据进行重构,通过进行多次实验,对不同的正交变换进行对比。
5.2. 实验结果及分析
1) 信号在不同正交变换下的稀疏度的表示
汇点接收到来自传感器节点的读数,通过压缩感知对数据进行重构,通过多次的实验,对不同的正交变换进行对比,发现可压缩性信号在不同的正交变换下具有不同的稀疏度,如图3所示,我们展示了8种不同场景的采样信号分别在离散傅里叶变换、离散余弦变换、小波变换、Row-trans变换、Col-trans变换下具有不同的稀疏度,从图中可以看出在离散傅里叶变换和离散余弦变换下信号的稀疏度不太显著,小波变换居中,而在Row-trans变换、Col-trans变换下信号的稀疏性更强。
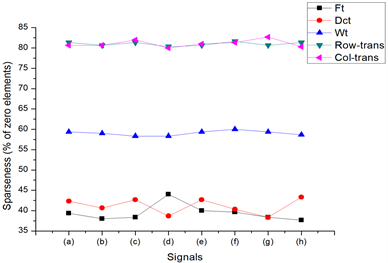
Figure 3. The sparsity of sampling signals of different scene under different orthogonal transformations
图3. 不同场景的采样信号在不同的正交变换下的稀疏度
2) 真实信号在不同正交变换下的重构误差
采样信号在不同的正交变换下具有不同的重构误差,如图4所示,我们计算了不同场景的采样信号分别在离散傅里叶变换、离散余弦变换、小波变换、Row-trans变换、Col-trans变换下的重构误差,我们发现在Row-trans变换、Col-trans变换下的重构误差优于其他三种正交变换。
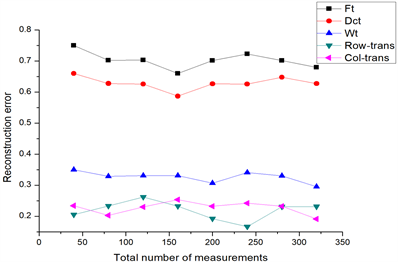
Figure 4. Reconstruction error of sampled signals under different orthogonal transforms
图4. 不同正交变换下采样信号的重构误差
3) 合成信号在不同正交变换下的重构误差
在一个拥有100个节点无线传感器网络中,参数值设定如下: , 。在图5中,我们展示了在1800次实验测量中,合成信号在不同的正交变换下的重构误差。我们发现离散余弦变换重构误差不太稳定,且误差较大,而傅里叶变换、小波变换、Row-trans变换、Col-trans变换重构误差比较稳定,且误差较小,Row-trans变换、Col-trans变换明显优于其他几种变换。
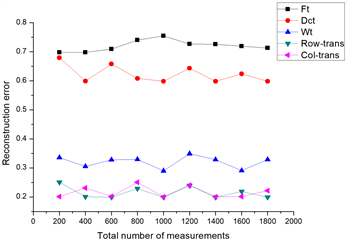
Figure 5. Reconstruction error of synthesized signals under different orthogonal transforms
图5. 不同正交变换下合成信号的重构误差
6. 结论及未来的工作
在本文中,我们主要对压缩感知中的信号稀疏表示进行了研究。文章主要采集了两种信号:人工合成信号以及8种不同场景的真实信号,为了更好地研究信号的稀疏性,自己设计了Row-trans变换、Col-trans变换进行稀疏变换,通过实验,可以发现在离散傅里叶变换和离散余弦变换下信号的稀疏度不太显著,小波变换居中,而在Row-trans变换、Col-trans变换下信号的稀疏性更强,并且其重构误差比较稳定,误差值较小,明显优于其他几种正交变换。但是文章仍旧存在许多不足,现有的压缩感知的路由的随机模型表述不够清晰,路由策略如何影响压缩感知的策略不够完备,我们需要进一步研究路由策略,以使整个网络能量均衡且延长网络生命周期。此外,压缩感知采用 最小化恢复算法,但其会迭代很多次,计算量比较大。因此,如何在较少的迭代下重构信号是我们接下来的研究目标。
基金项目
浙江省自然科学基金资助项目(No.LY16F020005)。
文章引用
李瑞晴,王 晖. 大规模无线传感器网络中稀疏信号的数据收集策略
The Data Collection Scheme for Sparse Signals in Large-Scale Wireless Sensor Networks[J]. 计算机科学与应用, 2019, 09(03): 551-564. https://doi.org/10.12677/CSA.2019.93063
参考文献
- 1. Gupta, P. and Kumar, P.R. (2000) The Capacity of Wireless Networks. IEEE Transactions on Information Theory, 46, 388-404. https://doi.org/10.1109/18.825799
- 2. Birkhauser, A. (2010) Mathematical Introduction to Compressive Sensing. University of Maryland, College Park, MD, USA, 1-33.
- 3. Bajwa, W., Haupt, J., Sayeed, A. and Nowak, R. (2006) Compressive Wireless Sens-ing. Proceedings of the International Conference on Information Processing in Sensor Networks (IPSN), Nashville, 19-21 April 2006, 134-142.
- 4. Baron, D., Duarte, M.F., Sarvotham, S., Wakin, M.B. and Baraniuk, R. (2005) An Information-Theoretic Approach to Distributed Compressed Sensing. Proceedings of the 43rd Allerton Conference on Communication, Control, and Computing, 28-30 September 2005.
- 5. Candès, E.J. and Romberg, J. (2006) Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information. IEEE Transactions on Information Theory, 52, 489-508. https://doi.org/10.1109/TIT.2005.862083
- 6. Candes, E.J. and Tao, T. (2006) Near-Optimal Signal Recovery from Random Projections: Universal Encoding Strategies? IEEE Transactions on Information Theory, 52, 5406-5424. https://doi.org/10.1109/TIT.2006.885507
- 7. Luo, C., Wu, F., Sun, J. and Chen, C.W. (2009) Compressive Data Gathering for Large-Scale Wireless Sensor Networks. Proceedings of ACM Mobicom’09, Beijing, 20-25 September 2009, 145-155. https://doi.org/10.1145/1614320.1614337
- 8. Elad, M. (2010) Sparse and Redundant Representations. The Technion-Israel In-stitute of Technology Haifa, Israel, 8-12. https://doi.org/10.1007/978-1-4419-7011-4
- 9. Quert, G., Masierot, R., Munaretto, D., Rossit, M., Widmer, J. and Zorzit, M. (2009) On the Interplay between Routing and Signal Representation for Compressive Sensing in Wireless Sensor Networks. 2009 Information Theory & Applications Workshop, San Diego, 8-13 February 2009, 1-10.
- 10. Liu, X., Luo, J. and Vasilakos, A.V. (2011) Compressed Data Aggregation for Energy Efficient Wireless Sensor Networks. 2011 8th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, Salt Lake City, 27-30 June 2011, 46-54.
- 11. Guo, L., Beyah, R. and Li, Y. (2011) SMITE: A Stochastic Compressive Data Collection Protocol for Mobile Wire-less Sensor Networks. 2011 Proceedings IEEE INFOCOM, Shanghai, 10-15 April 2011, 1611-1619. https://doi.org/10.1109/INFCOM.2011.5934953
- 12. Zheng, H.F., Yang, F., Tian, X.H., Gan, X.Y. and Xiao, S.L. (2015) Data Gathering with Compressive Sensing in Wireless Sensor Networks: A Random Walk Based Approach. IEEE Transactions on Parallel and Distributed Systems, 26, 35-45. https://doi.org/10.1109/TPDS.2014.2308212
- 13. Wang, W., Garofalakis, M. and Ram-chandran, K. (2007) Distributed Sparse Random Projections for Refinable Approximation. 2007 6th International Symposium on In-formation Processing in Sensor Networks, Cambridge, 25-27 April 2007, 331-339. https://doi.org/10.1109/IPSN.2007.4379693
- 14. Liu, X.-Y., Zhu, Y.M., Kong, L.H., Liu, C., Gu, Y., Vasilakos, A.V. and Wu, M.-Y. (2015) CDC: Compressive Data Collection for Wireless Sensor Networks. IEEE Transactions on Parallel and Distributed Sys-tems, 26, 2188-2196. https://doi.org/10.1109/TPDS.2014.2345257
- 15. Ebrahimi, D. and Assi, C. (2014) Compressive Data Gathering Using Random Projection for Energy Efficient Wireless Sensor Networks. Ad Hoc Networks, 16, 105-119. https://doi.org/10.1016/j.adhoc.2013.12.004
- 16. Baron, D., Sarvotham, S. and Baraniuk, R.G. (2010) Bayesian Compressive Sensing via Belief Propagation. IEEE Transactions on Signal Processing, 58, 269-280. https://doi.org/10.1109/TSP.2009.2027773
- 17. Li, P., Hastie, T.J. and Church, K.W. (2006) Very Sparse Random Projections. Proceedings of the ACM International Conference on Knowledge Discovery and Data Mining, Philadelphia, 20-23 August 2006, 287-296. https://doi.org/10.1145/1150402.1150436
- 18. Haupt, J., Bajwa, W.U., Rabbat, M. and Nowak, R. (2008) Compressed Sensing for Networked Data. IIEEE Signal Processing Magazine, 25, 92-101. https://doi.org/10.1109/MSP.2007.914732
- 19. Strang, G. (2003) Introduction to Linear Algebra. Third Edition, Massachusetts Institute of Technology, 184-201, 352-359.
- 20. Anna, N. and NoraDanil, M. (2004) Convex Optimization. Cambridge University Press, Cambridge, 1-8.