Advances in Social Sciences
Vol.
08
No.
11
(
2019
), Article ID:
32974
,
9
pages
10.12677/ASS.2019.811255
Research on Competitiveness of Some Countries Based on Principal Component Analysis and K-Means Clustering
Zewei Zhang, Xiang Yuan
School of Economics & Management, Shanghai Maritime University, Shanghai
Received: Oct. 25th, 2019; accepted: Nov. 8th, 2019; published: Nov. 15th, 2019

ABSTRACT
In this paper, 20 evaluation indicators from 42 countries are selected. Firstly, the information entropy reflecting the degree of information disorder is used to preliminarily screen the indicators, and 12 indicators with high contribution rate are retained, thus achieving the effect of dimensionality reduction. Then the principal components representing most information are obtained by the principal components analysis and the results are clustered by K-means method. Finally, the ranking and classification of national competitiveness are obtained.
Keywords:Information Entropy, Principal Components Analysis, K-Means Clustering, National Competitiveness
基于主成分分析的国家竞争力研究
张泽伟,袁象
上海海事大学经济管理学院,上海
收稿日期:2019年10月25日;录用日期:2019年11月8日;发布日期:2019年11月15日

摘 要
本文选取42个个国家的20个评价指标,首先用反映信息无序度的信息熵对指标初步筛选,保留贡献率较高的12个指标,达到降维的效果。再用主成法求得能代表大多数信息的主成分,用K-means法对结果进行聚类。最后得到国家竞争力的排名与分类。
关键词 :信息熵,主成分分析,K-Means聚类,国家竞争力

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
国家竞争力是指国家借助经营原有资产,形成自有的经济、社会模式来增加财富。国家竞争力不是一个单一的概念,而是由多种因素相互作用构成。瑞士洛桑国际管理学院认为经济实力、国际化程度、政府管理、金融体系、基础设施、企业管理、国民素质等八大因素是影响国家竞争力的主要因素。
迈克尔·波特 [1] 在《国家竞争优势》中提到,国家竞争力主要是由社会、经济结构、文化、制度等多个因素综合作用下形成并不断发展。Jay van Wyk (2010) [2] 在钻石模型的基础上构建了“双钻石”模型,它和“单钻石”模型的不同之处是,它纳入了影响国家竞争力的国际和国内决定性因素。易顺、韩江波 [3] 通过研究2010~2012年国外学者关于国家竞争力的文献,阐述竞争力影响因素,并进行实证剖析。魏海燕 [4] 对《世界竞争力年鉴》的评价指标体系的构成、演变和其中所包含的科技指标状况进行分析。
本文依据上述研究现状,建立国家竞争力评价指标体系。同时参考基于主成分分析的国内城市竞争力研究方法 [5] [6] 进行国家竞争力综合评价。由于原始指标数据可能存在冗余或不相关属性,先利用信息熵对数据预处理和降维。
2. 研究方法
建立国家竞争力指标的数学模型,假设X是已知的评价矩阵,其中元素 表示第i个国家的第j个指标。对于国家竞争力的评价问题,其评价数据包括多种类型,例如人均国内生产总值、国际互联网用户等评价指标的数据为绝对数值,而全球化指数、人文发展指数为相对数值。因此要先消除不同数据间量纲上的差异性。
1) 对评价矩阵X消除量纲并做归一化处理后得到计算矩阵Y:
其中 ,, 分别表示矩阵X的第j列最大值,最小值和平均值。
2) 然后计算每个指标的熵值,其中第j个指标的熵值为:
(式1)
取负号是要保证熵值为正,归一化系数定义为 。
3) 计算评价指标权重为:
(式2)
2.1. 指标体系构建
根据科学性、综合性等原则,结合国家竞争力评价的实际情况,本文构建的评价指标体系,见表1。
Table 1. Index system of national competitiveness evaluation
表1. 国家竞争力评价指标体系
2.2. 信息熵
在信息论中,信息熵用来刻画信息的无序度,熵越大表示信息的无序化程度越高,能够提供更多的信息就越多;相反,信息熵越小,则说明集合内的元素较为单一,所提供的信息较少。
2.3. 主成分分析
主成分分析法的降维思想和多标准评价指标的要求十分接近,因而近年来被大量的应用于社会学,公共管理和经济学等领域的评价体系中,成为一种独具特色的多指标评价方法。英国统计学家斯格特在对英国城镇发展水平做研究时,得到了57个综合指标。通过主成分法发现,仅需要5个由原始变量线性组合而成的新变量,就能以95%的精度来表示原始数据的差异性,数据维度得到了大幅下降。
2.4. K-Means聚类
聚类分析是通过距离来衡量数据之间的相似度从而实现类的划分。它是把n个对象根据它们的属性不同分为k个聚类,且使获得的聚类满足以下要求:同一聚类中的对象相似度最高;不同聚类中的对象相似度较低。
3. 实证分析
3.1. 数据来源
本文从国际统计年鉴(2016)获取42个国家竞争力综合测量指标数据,将20个指标变量的名称依次记为 。
3.2. 利用信息熵对指标变量进行初步筛选
依据公式(2-1)计算42个国家20项指标的熵值分别为:
再由公式(2-2)计算权重得:
由计算结果我们可以得到以下结论:
根据所求得得信息熵可以对维数进行初步的筛选,在总共20个评价指标中,第1,2,3,4,7,11,14,20这8个指标对评价的贡献率较低,因此在后面的数据分析只保留剩下的12个指标。
结合原始变量发现:第2项,即第三产业对国内生产总值增长的贡献率所占的权重最低,对整个评价体系的影响可以忽略;第11项,即国内生产总值的贡献率所占权重也较低,可能受庞大的人口基数影响。同时,我们看到第16项评价指标,人均国内生产总值,它所占的权重达到了0.065,仅此于第9项全球创新指数,可见用人均国内生产总值对国家竞争力的影响很大。另外,居民消费率和万美元国内生产总值能耗对评价结果的影响也很低;劳动参与率,移动电话数,人均寿命以及国内生产总值增长率对评价结果的影响较低,说明其有一定的参考价值,但特征不是很明显。例如,从移动电话数的原数据可以看出,虽然整体服从发达国家高于发展中国家,但也存在较多个例,如柬埔寨、越南、哈萨克斯坦等发展中国家的数据高于加拿大、美国、法国等发达国家。这与通常所认为的事实恰好相反。
通过对实例的计算分析,发现对评价体系的信息熵计算权重,得到的结果客观有效,可以较好的排除评价体系中部分对结果影响较小的评价指标。
本文中由于维数较低,用信息熵筛选时,维数减少不是很明显,如果处理一个1000维的数据集,设定信息熵阈值进行筛选,同时调节阈值来选取主元,例如设定阈值为0.52,满足条件的仅有43个变量,这使得变量个数大大降低。
3.3. 利用主成分分析对指标变量进行降维
利用R软件对筛选后的12个变量进行主成分分析,从相关矩阵求解,得到特征值和特征向量,分析方差贡献率,选取解释足够方差的主成分,并列出主成分得分,得到主成分线性组合并计算主成分得分。
3.3.1. 求出12个变量的相关系数矩阵,特征值和特征向量
将筛选后的数据定义为矩阵Z,求其相关系数矩阵,特征值和所对应的特征向量。求得特征值的平方为 ,相关系数矩阵所表2示。
3.3.2. 主成分分析
由表3可以看出,第1个特征值的方差贡献率为76.8%,第2个特征值的方差贡献率为6.8%,前三个主成分已经贡献了88.1%,因此可以保留三个主成分。
由主成分系数矩阵可得3个主成分的线性组合如下:
其中, ,,,,,,,,,,, 表示对原始变量标准化后的变量。
Table 2. Correlation matrix
表2. 相关系数矩阵
Table 3. Contributing rate of principal component
表3. 主成分贡献率
主成分的意义可由线性组合中系数较大,即权重较大的几个指标的综合意义来解释,所以 主要是知识经济水平,人文发展指数,国际互联网用户,全球创新指数,人均国内生产总值这6个指标的综合反映,它更多反映的是一个国家或地区的软实力。评价国家的综合实力除了单一经济实力外,还有很多涉及文化,教育等方面的因素。这些因素也是构成国家综合实力的重要表现。软实力通常都是由经济做保障的,软实力强的国家其经济实力也通常都比较强。用 来评价国家竞争力已经有76.8%的把握,所以这6个指标是反映国家竞争力的主要指标,每一项都必不可少。 和 主要是企业经营合同手续个数,高等教育粗入学率的综合反映,它标志着国家的企业经济水平和人才教育水平。
3.3.3. 主成分得分
各国家竞争力评价得分及排序见表4所示。
Table 4. Scoring and ranking of national competitiveness evaluation
表4. 国家竞争力评价得分及排序
在主成分得分中,正负不代表大小,仅表示该国家的竞争力与平均水平的位置关系,以国家竞争力的平均水平算作零点。在这个例子中,应该定义为:得分为正的国家其竞争力在平均水平以下;而得分为负的国家,其竞争力在平均水平以上。
为了更加客观的表示各国主成分得分情况,作出其双投影图,如图1所示。图中的数字表示对应编号的国家,矢量在坐标上的投影则是该变量对主成分的载荷,它解释了原始变量和主成分相关性强弱的问题:红线在横坐标上的投影是各变量对第一主成分的载荷;在纵坐标上的投影是各变量对第二主成分的载荷。
结合排序表和双投影图对整体进行分析可以看出,各样本已经得到了粗略的分类结果。空间上相距越近的变量,正相关程度越高,国家竞争力水平越相近;距离原点越远说明这个变量被这两个主成分解释的越充分。可以看出,在第一主成分上,各个变量在横坐标上的投影相差不大,即载荷相差不大,各变量解释第一主成分的权重相似。相对而言,第15个变量的载荷最大,第18个变量的载荷系数与其它变量相反。对于第二主成分,第12,18,19个变量的投影较大,其载荷大,也就是说这三个变量描述了更多的第二主成分。
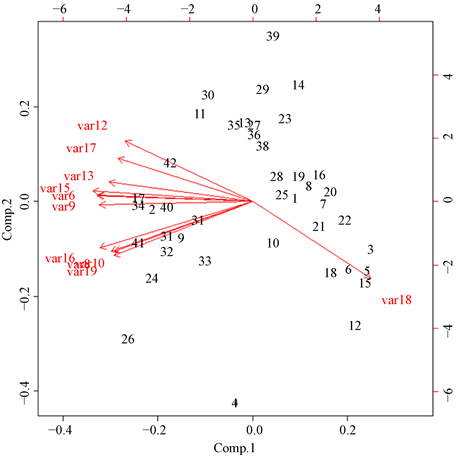
Figure 1. Double projection
图1. 双投影图
分布在第三象限的第一主成分较好的是{26,41,34,17,24,2,40,32,31,42,9}对应国家是{美国,澳大利亚,荷兰,新加坡,加拿大,瑞士,英国,德国,法国,新西兰,日本},这些国家的竞争力强,人均国内生产总值高,人类发展指数高,人均寿命高,城市人口比重高,全球化指数高。而第一主成分得分较差的,即位于第四象限的样本{18,22,6,12,15,5,3}对应国家{斯里兰卡,尼日利亚,印度,老挝,巴基斯坦,柬埔寨,孟加拉国},这些国家的竞争力最弱。这些国家由于底子薄弱,工业基础差,商业不够发达,经济发展缓慢,部分地区还存在政局不稳定。
3.3.4. K-Means聚类
取聚类数为4,根据主成分得分的K-means聚类结果画出散点图,如图2所示,数据为聚类结果集的列“Comp.1”和“Comp.2”,颜色为用1,2,3,4表示缺省颜色,并用直线加以划分,从左往右一次是第一至第四区域,分别表示第一至第四聚类。由此将样本中的42个国家和地区分为以下四类:
黑点表示的是第一聚类,包括{美国,荷兰,新加坡,瑞士,加拿大,英国,德国,法国,新西兰,日本,澳大利亚,西班牙,比利时,意大利};国家竞争力强,是高度发达的资本主义国家和地区。主要分布在欧洲中西部,北美,澳洲及亚洲日本。
蓝点表示的是第二聚类,包括{文莱,韩国,马来西亚,阿根廷,巴西,委内瑞拉,捷克,波兰,俄罗斯,土耳其,乌克兰};国家竞争力较强,主要分布在南美洲,马来群岛,东欧等地。
红点表示的是第三聚类,包括{印度尼西亚,伊朗,哈萨克斯坦,蒙古,菲律宾,泰国,越南,埃及,南非,墨西哥};国家竞争力一般,分布范围广泛。
绿点表示的是第四聚类,包括{孟加拉国,柬埔寨,印度,老挝,巴基斯坦,斯里兰卡,尼日利亚},国家竞争力弱主要分布在非洲,南亚,中南半岛等地。
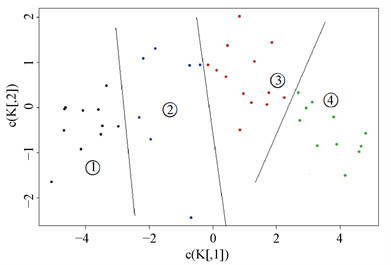
Figure 2. K-means clustering scatter
图2. K-means聚类散点图
4. 对实例的相关思考
事实上,权威的国家竞争力评价报告IMD是基于经济学理论,应用统计指标和问卷调查结果构建系统的综合评价指标体系,对国家和地区在国际上综合竞争能力进行测度。然而IMD的评价指标极其复杂,分为多个层次的评价指标,共采用了超过300个的竞争力指标。在实际的数据获取中会比较困难,本文只列出了20个竞争力指标,但最后的分析结果与当前的权威排名拟合的较好,发达国家和发展中国家得以区分。对于300个指标的分析,同样可以采取基于信息熵的主成分法。对于K-means聚类的类数选取也是一个值得思考的问题,可以通过计算轮廓系数确定,但是有时需要根据应用场景进行调整,而不能完全的依据评估参数选取。
国家竞争力评价带来的是一个横向比较的国际化视野,IMD指标体系是从一个国家的竞争力得分情况来评价该国的竞争力,体现的是基于竞争结果的静态分析。这个评价体系反映的是已经形成的竞争力情况,而事实上,只研究一年度的评价结果并不能充分的反映一个国家竞争力,分析它可能潜在的能力。因此,在实际评价指标体系对国家竞争力进行测度和比较时,应该结合多年的评价结果和具体的国家国情,对其中的部分指标做适当修正和调整,以便更好的反映国家实力。
此外,也需要考虑客观存在的因素对评价结果的影响:例如(1) 人口因素对评价结果的影响,我国是个人口大国,人均指标结果往往被拉的很低;(2) 评价指标体系中数据采样方法对结果的影响。样本量过小或被调查者的个人偏好给整个评价体系带来了不可避免的系统误差,软指标越多,系统误差就可能越大,这也会造成评价结果在不同年度产生较大的波动。(3) 评价指标体系往往是以发达国家经验为基础制定的,对发展中国家参与国际比较有一定负面影响。
文章引用
张泽伟,袁 象. 基于主成分分析的国家竞争力研究
Research on Competitiveness of Some Countries Based on Principal Component Analysis and K-Means Clustering[J]. 社会科学前沿, 2019, 08(11): 1873-1881. https://doi.org/10.12677/ASS.2019.811255
参考文献
- 1. 迈克尔•波特. 国家竞争优势[M]. 北京: 华夏出版社, 2002.
- 2. Van Wyk, J. (2010) Double Diamonds, Real Diamonds: Botswana’s National Competitiveness Academy of Marketing Studies Journal, 14, 55-76.
- 3. 易顺, 韩江波. 国外国家竞争力研究: 理论架构与展望[J]. 兰州商学院学报, 2014(5): 93-102.
- 4. 魏海燕.《世界竞争力年鉴》评价体系研究及其思考[J]. 科技管理研究, 2013(5): 65-68+77.
- 5. 田美玲, 方世明. 汉江流域中心城市竞争力的评价及时空演变[J]. 统计与决策, 2016(9): 103-106.
- 6. 于丽英, 郭洪晶. 长江三角洲地区城市综合竞争力的评价研究[J]. 上海大学学报(社会科学版), 2011, 18(1): 79-90.
