Journal of Water Resources Research
Vol.3 No.04(2014), Article
ID:13947,6
pages
DOI:10.12677/JWRR.2014.34041
Threshold Autoregressive Model in Rainfall Forecasting—A Case Study in Yiwu
Department of Geography, Zhejiang Normal University, Jinhua
Email: *309442308@qq.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jul. 16th, 2014; revised: Jul. 23rd, 2014; accepted: Aug. 8th, 2014
ABSTRACT
The meteorological elements are not only combined effected by the impact factors, but also their own evolution. Multivariate analysis ignores the evolution of meteorological elements themselves, and the time-series analysis did not take full advantage of the implicit information about the impact factor. This article uses threshold autoregressive model by piecewise linearization method of nonlinear problem to deal with the meteorological elements, both considering influence factors of superimposition, and balancing the evolution law of meteorological elements themselves; the fitting and forecasting effect is relatively good. But now the time sequence of the meteorological elements is generally short, usually around 40 to 60 years, which belongs to the incomplete information system, the extrapolation value should not be too long. It would be best to gradually replenish the new information in a timely manner to improve the fitting and forecasting results.
Keywords:Precipitation, Impact Factor, Threshold Autoregressive, Forecasting

门限自回归模型在降水量预报中的应用
——以中国义乌市为例
朱灵子,冯利华*,黄 琼
浙江师范大学地理系,金华
Email: *309442308@qq.com
收稿日期:2014年7月16日;修回日期:2014年7月23日;录用日期:2014年8月8日

摘 要
气象要素既受影响因子的综合作用,又有自身的演变规律。但是,多元分析忽视了气象要素自身的演变规律,而时间序列分析没有充分利用影响因子的隐含信息。本文运用门限自回归模型通过逐段线性化手段来处理气象要素的非线性问题,既考虑影响因子的叠加作用,又兼顾气象要素自身的演变规律,其拟合和预报效果相对较好。但目前气象要素的时间序列普遍较短,一般都在40~60年左右,属不完全信息系统,其外推值不宜过长。最好能够逐年及时地补充新的信息,以改善拟合和预报效果。
关键词
降水量,影响因子,门限自回归,预报

1. 引言
由于水资源的时空分布不均、用水量的逐渐增长和水污染的日益严重,因此,目前许多国家都感到水源紧张,从而使人类面临水资源不足的压力和风险。事实上水荒问题已经悄然逼近,尤其是在一些干旱地区和大中城市[1] ,水资源危机正与日俱增,水资源短缺已成为全世界共同面对的难题[2] [3] 。因此,如何使经济发展与水资源互相协调已成为一个迫在眉睫的难题,区域水环境已遭遇到经济发展所面临的巨大挑战[4] 。
Box和Jenkins在1970年提出了处理线性时间序列的自回归模型AR(p)、自回归滑动平均模型ARMA(p, q) (Autoregressive and Moving Average)以及自回归求和滑动平均模型ARIMA(p, d, q) (Autoregressive Integrated Moving Average)[5] 。这些模型为处理线性时间序列提供了有力的数学工具。但是,实际工作中所遇到的数据序列往往非常复杂,有时候不能用线性模型来描述。因此,非线性模型的研究和应用越来越为人们所关注。Tong H于1972年提出的门限自回归(Threshold Autoregressive, 简称为TAR)模型就是一种处理非线性系统变化的时间序列模型[6] ,已经在气象学、水文学和地质学等领域获得了广泛的应用[7] [8] 。
义乌市位于中国浙江省的中部地区。20世纪90年代以来,义乌市的经济处于快速发展时期。但是,近年来义乌市出现了严重的水荒问题。义乌市的多年平均水资源总量为7.19亿m3,人均水资源量只有1073 m3,已经远远低于人均2000 m3的国际缺水警戒线。尤其是2003年夏季,出现了50a未遇的高温,夏旱连秋旱,7~10月的降水量只有219 mm,仅及正常年份的52%,2004年继续干旱[9] 。由于水库无水可放,因此供水部门对居民生活用水和单位、企业用水全部实行分时分段降压供水和定额供水,最少时每周只有9 h正常供水,4 d全天断水。居民用水苦不堪言,企业则被迫停产,水资源已成为制约义乌市经济发展的主要瓶颈。为此,早在2000年11月,义乌市就出资2亿元,每年向东阳市横锦水库永久性购买5000万m3的淡水资源,成为水利部提出“水权与水市场”理论后的第一笔水权交易。但是据预测,到2020年,义乌城乡将缺水1.57亿m3[9] 。因此,为了使义乌市的经济健康而稳步地增长,需要分析该区未来降水量的变化趋势。但是,降水量的时间序列十分复杂,是一种非线性系统,并且与前期影响因子的时间序列具有相关性。为此,拟利用门限自回归模型来对义乌市的降水量进行预报。
2. 方法
门限自回归是用门限对时间序列进行划分,选用不同的自回归模型来描述自然现象[5] 。门限自回归模型的基本思想是用分段线性化手段来处理非线性系统,而门限的控制作用保证了系统的稳定性。它有两个类型:
2.1. 单一门限自回归模型
对于某一气象要素的时间序列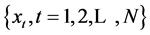 ,门限自回归模型为:
,门限自回归模型为:
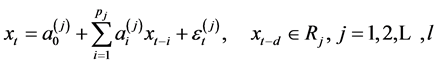 (1)
(1)
式中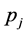 为第
为第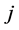 个门限自回归的阶,
个门限自回归的阶,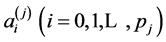 为第
为第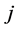 个门限自回归系数,
个门限自回归系数,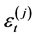 为白噪声,
为白噪声,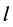 为模型个数。由于该模型描述了一个时间序列
为模型个数。由于该模型描述了一个时间序列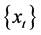 的非线性系统变化,故称为单一门限自回归模型,并简记为TAR
的非线性系统变化,故称为单一门限自回归模型,并简记为TAR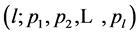 。
。
2.2. 混合门限自回归模型
由于气象要素的时间序列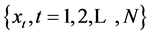 除了与自身的变化存在相关外,还可能与另一前期影响因子的时间序列
除了与自身的变化存在相关外,还可能与另一前期影响因子的时间序列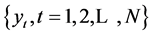 具有密切联系。那么此时的门限自回归模型为:
具有密切联系。那么此时的门限自回归模型为:
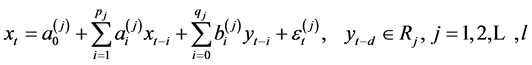 (2)
(2)
式中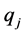 为第
为第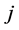 个门限自回归的阶,
个门限自回归的阶,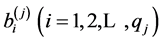 为第
为第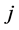 个门限自回归系数,其余符号意义同式(1)。由于该模型描述了一个具有前期影响因子相互作用的非线性系统变化,故称为混合门限自回归模型,并简记为TARSO
个门限自回归系数,其余符号意义同式(1)。由于该模型描述了一个具有前期影响因子相互作用的非线性系统变化,故称为混合门限自回归模型,并简记为TARSO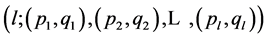 。
。
一般的非线性系统只能在一定的限制条件下建立特定的非线性模型,而门限自回归模型可以通过逐段线性化手段来处理气象系统的非线性问题,这也是该模型的一大优点。
门限自回归模型需要估计以下参数:
1) 延迟步长d;
2) 门限值r;
3) 自回归阶数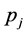 和
和 ,以及相应的自回归系数
,以及相应的自回归系数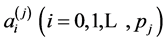 和
和 ,其中
,其中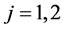 。
。
模型的自回归系数用线性最小二乘法估计最为方便。一般地说,延迟步长d、门限值r以及自回归阶数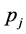 和
和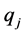 宜根据线性估计中的最小信息量准则——AIC准则进行统计识别。
宜根据线性估计中的最小信息量准则——AIC准则进行统计识别。
3. 参数确定
3.1. 确定最大延迟步长D
这里需要预先给定模型的最大阶数L。最大延迟步长D可根据物理分析或统计识别方法进行确定。令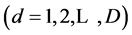
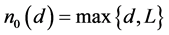 。对于固定的d,在不会引起混淆的情况下,将
。对于固定的d,在不会引起混淆的情况下,将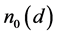 简记为
简记为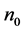 。
。
3.2. 确定门限值r
将 从小到大排列为
从小到大排列为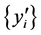 (即
(即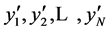 )。再把
)。再把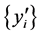 中下标分别为
中下标分别为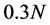 、
、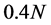 、
、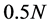 、
、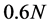 、
、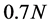 的相应数据作为门限候选值
的相应数据作为门限候选值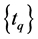 。对于每一门限候选值
。对于每一门限候选值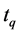 ,计算AIC
,计算AIC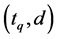 ,则
,则
 (3)
(3)
所对应的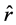 即为门限值
即为门限值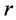 。
。
3.3. 确定模型系数及阶数
对于固定的r和d,将数据 分成两类。如果
分成两类。如果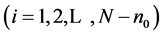
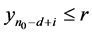 ,则
,则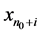 属于第一类,否则属于第二类。设第一类和第二类数据分别为
属于第一类,否则属于第二类。设第一类和第二类数据分别为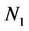 和
和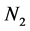 个,并用
个,并用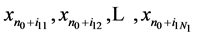 表示第一类数据,用
表示第一类数据,用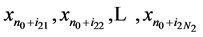 表示第二类数据。
表示第二类数据。
对于第一类数据考虑模型
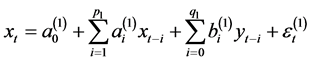 (4)
(4)
将第一类数据代入上式得
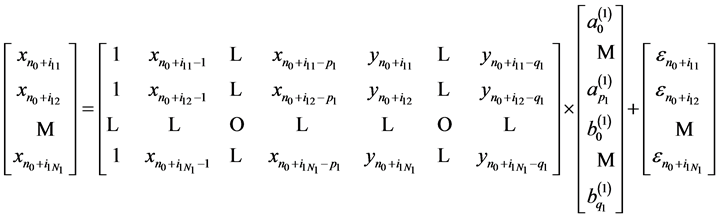 (5)
(5)
写成向量形式,即
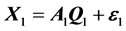 (6)
(6)
式中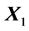 和
和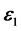 均为
均为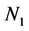 维向量,
维向量,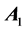 为
为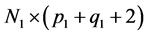 维矩阵,
维矩阵,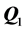 为
为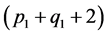 维向量。参数向量
维向量。参数向量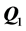 的最小二乘估计由下式求得
的最小二乘估计由下式求得
 (7)
(7)
残差平方和 和AIC分别为
和AIC分别为
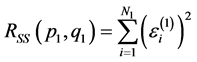 (8)
(8)
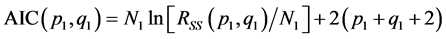 (9)
(9)
针对固定的d和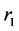 ,第一个模型的阶数可用AIC来确定,即
,第一个模型的阶数可用AIC来确定,即
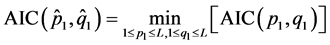 (10)
(10)
同理,对于第二类数据考虑模型
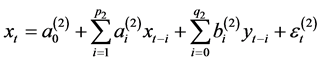 (11)
(11)
将第二类数据代入上式,可以求得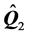 和
和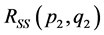 。从而可得
。从而可得
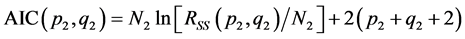 (12)
(12)
并利用AIC准则,确定第二类模型的阶数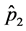 和
和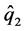 。
。
由于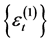 与
与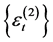 相互独立,故有
相互独立,故有
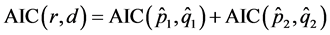 (13)
(13)
3.4. 确定延迟步长d
由于观测值的实际有效数字个数为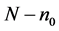 ,因此,
,因此,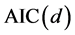 应取
应取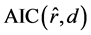 的规范值
的规范值
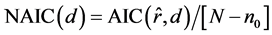 (14)
(14)
令
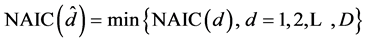 (15)
(15)
则 就是最优的延迟步长值。
就是最优的延迟步长值。
4. 结果与讨论
门限自回归模型对汛期降水进行预测时,会在重视水文过程自身演变规律的同时,又兼顾主要前期影响因子的作用,并通过逐段线性化手段处理水文系统的非线性问题。也是描述复杂水文过程的一种比较有效的模型。降水量的影响因素较多,根据现有研究表明,厄尔尼诺事件是一个主要的影响因子[10] 。为此,选用厄尔尼诺事件作为前期影响因子,利用门限自回归模型来对1959~2011年中国义乌市的降水量进行预报。
降水量的影响因素较多。现有研究表明,厄尔尼诺事件是一个主要的影响因子[10] 。为此,选用厄尔尼诺事件作为前期影响因子,利用门限自回归模型来对1959~2011年中国义乌市的降水量进行预报。
这里,义乌市降水量是指义乌市6月21日~7月5日的降水量。因为6月21日~7月5日是义乌市的平均暴雨集中期,该时段的降水量多少对义乌市全年水资源量的贡献至关重要。历年义乌市6月21日~7月5日降水量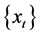 的数据来源于中国气象局国家气候中心。厄尔尼诺事件是赤道东太平洋上层海水异常增暖的现象。现在世界各国科学家对厄尔尼诺都给出了一个基本一致的定义:如果赤道东——中太平洋大范围的海温异常升高,月平均海表温度SST距平值达到+0.5℃、且持续3个月以上者,就称为一次厄尔尼诺事件。Nino 3区的海表温度是指在赤道东太平洋5˚S~5˚N、150˚W~90˚W范围内的海洋表层温度,它的异常升高就是厄尔尼诺事件。历年1月Nino 3区海表温度距平
的数据来源于中国气象局国家气候中心。厄尔尼诺事件是赤道东太平洋上层海水异常增暖的现象。现在世界各国科学家对厄尔尼诺都给出了一个基本一致的定义:如果赤道东——中太平洋大范围的海温异常升高,月平均海表温度SST距平值达到+0.5℃、且持续3个月以上者,就称为一次厄尔尼诺事件。Nino 3区的海表温度是指在赤道东太平洋5˚S~5˚N、150˚W~90˚W范围内的海洋表层温度,它的异常升高就是厄尔尼诺事件。历年1月Nino 3区海表温度距平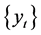 的数据来源于中国气象局国家气候中心。
的数据来源于中国气象局国家气候中心。
根据预报要求,将1959~2008年的降水量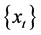 作为拟合样本,2009~2011年的降水量
作为拟合样本,2009~2011年的降水量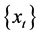 作为检验样本。为了减小原始数据
作为检验样本。为了减小原始数据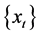 与
与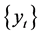 的数量级差异,对
的数量级差异,对 作对数处理,而对
作对数处理,而对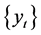 不作处理。计算时,预定模型的最大阶数
不作处理。计算时,预定模型的最大阶数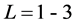 ,最大延迟步长
,最大延迟步长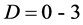 ,由此组成了不同的预报方案。
,由此组成了不同的预报方案。
对于未考虑前期影响因子相互作用的单一门限自回归模型,根据AIC准则,经过计算,可以得到:当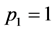 、
、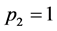 、
、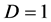 时,预报方案为最佳,即TAR(2, 1, 1)。那么义乌市降水量的单一门限自回归模型为:
时,预报方案为最佳,即TAR(2, 1, 1)。那么义乌市降水量的单一门限自回归模型为:
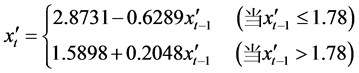 (16)
(16)
式中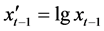 。
。
对于考虑前期影响因子相互作用的混合门限自回归模型,根据AIC准则,经过计算,可以得到:当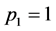 、
、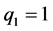 、
、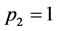 、
、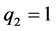 、
、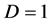 时,预报方案为最佳,即TARSO(2, (1, 1), (1, 1))。那么义乌市降水量的混合门限自回归模型为:
时,预报方案为最佳,即TARSO(2, (1, 1), (1, 1))。那么义乌市降水量的混合门限自回归模型为:
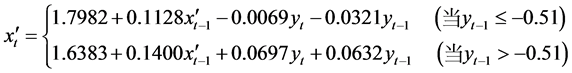 (17)
(17)
式中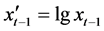 。
。
从表1中可以看到,TAR(2, 1, 1)的最大绝对误差为45,平均绝对误差为33.0,最大相对误差为83.3%,平均相对误差为41.4%。而TARSO(2, (1, 1), (1, 1))的最大绝对误差为28,平均绝对误差为18.7,最大相对误差为44.4%,平均相对误差为22.6%。可见TARSO(2, (1, 1), (1, 1))的误差都比TAR(2, 1, 1)的误差小。
由此表明,选用厄尔尼诺事件作为前期影响因子,可以明显地减小义乌市降水量的预报误差。究其原因在于:当厄尔尼诺事件出现时,信风减弱,西太平洋的表层暖水迅速向东蔓延,东太平洋地区的冷水上翻作用随之减弱,这样赤道太平洋的海表温度在西部下降,东部上升,以致亚洲季风偏弱。在厄尔尼诺事件期间,低纬地区的瓦克环流减弱,相应低层东风也减弱。原来在西太平洋上的强对流活动区移至中太平洋地区,以致热带幅合带活动减弱、位置偏南,从而使义乌市降水量明显增多。反之,当厄尔尼诺事件消失时,义乌市降水量明显减少。但目前的门限自回归模型仅能考虑一个主要的前期影响因子,因此影响因子的信息量损失较大,对长期气象预报来说具有一定的局限性。在门限自回归模型中如何考虑多个影响因子的综合作用,还有待于进一步深入研究。
气象要素变化的分析方法主要有两类:多元分析法和时间序列分析法。前者是通过气象要素与影响因子的统计关系来进行预报的,后者是通过气象要素自身的演变规律来进行预报的。判别分析、聚类分析、回归分析和主成分分析等均属于多元分析法,其中又以回归分析应用最为广泛。谱分析、周期分析、自回归分析和马尔可夫链等均属于时间序列分析法,其中应用较多的是自回归(AR)模型和自回归滑动平均(ARMA)模型。
事实上,气象要素既受影响因子的综合作用,又有自身的演变规律。但是,多元分析忽视了气象要素自身的演变规律,而时间序列分析没有充分利用影响因子的隐含信息。因此,就目前的实际情况而言,无论是拟合精度还是预报效果,两类方法都不同程度地出现时好时坏的现象,令人难以满意。而门限自回归模型既能够考虑影响因子的叠加作用,又能够兼顾气象要素自身的演变规律,并通过逐段线性化手段来处理气象要素的非线性问题。
5. 结语
门限自回归模型是将回归模型(多元分析)与自回归模型(时间序列分析)结合起来的混合模型。与回归模型和自回归模型相比,门限自回归模型能够更好地反映气象要素的非线性变化特征,其拟合和预报效果相对较好。
表1. 义乌市6月21日~7月5日TAR(2, 1, 1),TARSO(2, (1, 1), (1, 1))的预报值及其误差
气象要素的长期变化是多个影响因子综合作用的结果。但目前的门限自回归模型仅能考虑一个主要的前期影响因子,因此影响因子的信息量损失较大,对长期气象预报来说具有一定的局限性。在门限自回归模型中如何考虑多个影响因子的综合作用,还有待于进一步深入研究。
对于天气气候预报问题,气象中有动力和统计两种方法。动力方法认定天气气候的变化属于确定论的研究范畴,而统计方法认定这一变化是概率论的研究范畴,存在不确定性。统计方法实质上是一种数据分析方法,它利用了大量的实况数据资料,但没有利用或充分利用物理知识。目前,降水预测主要还是统计学方法,在大量的预测实践中,人们也认识到:通过纯统计方法的改进,已很难使长期降雨预测的水平再有根本性的提高,而动力数值模式预测虽被公认是今后发展的方向,但由于对长期天气过程形成的物理机制尚不太明确,因而动力数值预测的发展还存在着许多困难。因而从预报方法上,动力和统计相结合,取长补短,是解决汛期降水预报的有效发展方式。
基金项目
国家自然科学基金资助项目(41171430)。
参考文献 (References)
- [1] FENG, L. H., SANG, G. S. Change trend of water resources using matter analysis. Human & Ecological Risk Assessment, 2012, 18(4): 933-942.
- [2] HAJKOWICZ, S., HIGGINS, A. A comparison of multiple criteria analysis techniques for water resource management. European Journal of Operational Research, 2008, 184(1): 255-265.
- [3] PAVLIS, M., CUMMINS, E. and MCDONNELL, K. Groundwater vulnerability assessment of plant protection products: A review. Human and Ecological Risk Assessment, 2010, 16(3): 621-650.
- [4] GUPTA, A. S., JAIN, S. and KIM, J. S. Past climate, future perspective: An exploratory analysis using climate proxies and drought risk assessment to inform water resources management and policy in Maine, USA. Journal of Environmental Management, 2011, 92(3): 941-947.
- [5] ZHENG, Z. C., WANG, Z. T. BASIC programme storerooms of practice prediction methods. Guangzhou: Sun Yat-sen University Press, 1985: 209-280.
- [6] TONG, H. Threshold models in nonlinear time series analysis. Lecture Notes in Statistic, No. 21, New York: Springer Verlag, 1983.
- [7] JIAN, W. B. Application of non-linear time series model in simulation of spring discharge regime. Site Investigation Science and Technology, 1989, (5): 39-42.
- [8] GAO, J. T., TJOSTHEIM, D. and YIN, J. Y. Estimation in threshold autoregressive models with a stationary and a unit root regime. Journal of Econometrics, 2013, 172(1): 1-13.
- [9] FENG, L. H., LUO, G. Y. Application of possibility-probability distribution in assessing water resource risk in Yiwu city. Water Resources, 2011, 38(3): 409-416.

NOTES
作者简介:朱灵子(1990-),女,安徽宣城人,在读硕士研究生,研究方向:水文学与水资源。
*通讯作者。
