Modeling and Simulation
Vol.07 No.02(2018), Article ID:25214,7
pages
10.12677/MOS.2018.72012
Calibration of Car-Following Model Based on Cross-Entropy Method
Kaiyan Fu1, Jiandong Qiu1, Jiajie Pan2
1Shenzhen Urban Transport Planning Center Co., Ltd., Shenzhen Guangdong
2Traffic Information Engineering & Technology Research Center of Guangdong Province, Shenzhen Guangdong
Received: May 5th, 2018; accepted: May 23rd, 2018; published: May 30th, 2018

ABSTRACT
Calibration of car following models seeks for a more realistic representation of car following behavior in complex driving situations to improve traffic safety and to better understand several puzzling traffic flow phenomena, such as stop-and-go oscillations. However, calibrating these models is never a trivial task. This is caused by the fact that some parameters are generally not directly observable from traffic data. Moreover, conventional deterministic calibration methods always result in a large number of local optima. This contribution puts forward a framework of calibration based on Cross-Entropy Method (CEM), which approaches the optimal probability density function with monte carlo and important sampling strategy. Empirical cases calibrate the intelligent driving model with synthetic data and NGSIM data. The results not only verify the ability of CEM to search global optima, but also confirm the great potential of CEM to adopt into actual traffic measurements.
Keywords:Car-Following Models, Model Calibration, Cross-Entropy Method, Global Optima
基于交叉熵算法的跟驰模型标定
傅恺延1,丘建栋1,潘嘉杰2
1深圳市城市交通规划设计研究中心有限公司,广东 深圳
2广东省交通信息工程技术研究中心,广东 深圳
收稿日期:2018年5月5日;录用日期:2018年5月23日;发布日期:2018年5月30日

摘 要
跟驰模型的标定是为了更好地重现真实驾驶情况从而增强交通安全和分析如停-走间断流等复杂的交通流情况。然而,跟驰模型的标定并不是一件容易的事。这是因为某些参数是不能从交通流数据中直接观测得到。此外,传统的确定性标定方法会导致大量局部最优值的出现。在此基础上,本文提出了基于交叉熵算法的跟驰模型标定的框架,基于蒙地卡罗与重要样本策略逐步逼近参数的最优概率密度函数。实例分别采用合成数据与实测数据标定智能驾驶模型,验证了交叉熵算法搜索全局最优值的能力,并体现了交叉熵算法适用于实测交通流数据标定的潜能。
关键词 :跟驰模型,标定,交叉熵算法,全局最优值

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在进行交通规划和交通决策投入使用之前,精确地重现特定交通场景上的交通行为将会为交通工作者提供极大的帮助。因此,交通微观模型,特别是跟驰模型,在模拟复杂的交通场景,例如交通事故现场、交通信号灯控制等方面得到了广泛的应用 [1] [2]。然而,不同交通场景上的交通行为存在着极大的差异,并且,即使在同一交通场景中,早上与晚上的交通行为也截然不同。因此,能极大地提高跟驰模型重现特定交通场景上交通行为描述能力的参数标定是必不可少的。然而,交通仿真模型的描述能力越强,表征的交通状态越多,模型内部结构越复杂,所需标定的参数也越多,参数标定过程也越困难。首先是交通仿真模型的绝大部分参数是不能够从交通数据中直接观测得到,比如微观跟驰模型中的驾驶员反应时间、期望速度、期望间距等;其次,不同类型的道路传感器的检测原理与结构互不相同,导致检测的交通数据往往存在不同程度的误检甚至漏检的情况;最后,通过最小化模型输出与观测数据之间的差异构建的模型标定优化问题,往往存在着大量的局部最优解 [3] [4] [5]。上述情况都在不同程度上加剧交通模型标定的难度,导致模型描述性能得不到充分的体现。
交通模型的参数标定通常是求解最小化模型输出值与观测数据值之间差异的模型参数最优值的过程。然而由于模型的复杂结构与参数之间的关联作用,导致了传统求解算法如梯度下降法等不再适用。因此,越来越多的交通模型采用随机搜索算法进行参数的标定。该类算法的主要思想是把参数可行域划分为多个子集,按照一定的原理将参数逐步迭代至全局最优值附近。随机搜索法包括模拟退火算法、多启发式算法、遗传算法等 [3] [4] ,均在交通模型标定应用中获得准确的参数最优值。值得注意的是,Ciuffo和Punzo采用“No Free Lunch”理论去评估以上各类算法在微观交通模型的标定中的性能 [4]。经过多次实验,他们发现,影响算法在标定方面的性能有多个因素,其中包括要标定的参数类型、选用给的适合度指标、交通流数据的质量等。此外,分析表明,在Ciuffo和Punzo的实例中,遗传算法表现出最为优异的性能。然而,遗传算法的计算集约以及无法证明收敛性的诟病限制了它的使用,并且遗传算法的收敛方向随机且不稳定,常常需要大量的迭代次数满足弱收敛条件 [6]。
近期研究表明,交叉熵算法作为一种新兴的算法,不仅可以求得组合优化问题的全局最优值,并且计算效率极高,算法收敛性可证 [7] [8] [9]。为此,本文提出基于交叉熵算法的跟驰模型参数的标定框架,利用合成数据标定验证交叉熵算法的全局搜索能力,采用NGSIM的路径数据标定体现交叉熵算法的普遍适用性,为交通模型标定提供可行高效的新颖解决框架。
2. 智能驾驶模型
跟驰模型研究的对象是跟车对,一组或多组,包括前车和后车。研究的目标是利用数学模型精确地描述车辆在交通场景上的驾驶行为,主要包括车辆在自由流路段中加速至期望速度的行为、过于靠近前车或者障碍物时的减速行为、与前车保持一定距离时的匀速行为等。因此,传统的跟驰模型中后车的行为主要由几个参数决定,包括间隔时间、间隔距离、前车的速度和加速度等。
智能驾驶模型是其中得到了广泛的接受和使用的模型之一 [10]。该模型考虑了期望速度以及期望空间间距去模拟后车的加速或减速行为。
(1)
其中,a表示最大加速度, 表示期望速度, 表示空间间距(前车的后保护栏到后车的前保护栏之间的距离), 表示期望空间间距。当后车与前车相距较远时,公式(1)中的第三项将可忽略不计,此时该模型表现为由最大加速度以及期望速度主导的自由加速模型: , 表示后车速度。当后车靠近前车时,减速策略( )将占主导作用防止瞬时空间间距 过于靠近期望空间间距 。
(2)
其中, 表示最小空间间距, 表示前车与后车速度的差值,b表示期望减速度,T表示期望时间间隔。值得注意的是,智能驾驶模型的减速策略会在两车的空间间隔很小时产生很大的减速度,由此保证两车不会相撞。
终上所述,智能驾驶模型要标定的参数包括最大加速度a,期望减速度b,期望速度 ,期望时间间隔T,以及最小空间间距 。值得注意的是,以上5个参数都不能从交通流数据中直接观测得到,并且各个参数的标定对应着各自的交通场景。具体来说,最大加速度和期望减速度与停-走的交通流相关,期望时间间隔主要与稳定的跟车交通状态有关,期望速度在自由流交通状态下可标定,最小空间间距则要求爬行或者停止的交通状态。换句话说,用于标定智能驾驶模型的交通流数据建议包括以上提及的各类交通状态。
3. 交叉熵算法
交叉熵算法是一种相对较为新颖的离线全局优化算法,基于传统的蒙地卡罗方法,集中解决复杂的仿真和优化问题。就方法论来说,交叉熵算法的迭代结构虽然简单,但是具有较为完整的理论基础,并且适用于不同类型的组合优化问题求解以及小概率时间的估计,其中包括缓冲区分配问题、电信系统的排队模型、神经计算等领域。在交通领域,交叉熵算法解决了在交叉口如何分配绿灯时间可以使得总体延误最小的问题,以及在城市交通网络中考虑路径选择的信号配时问题等 [8] [11]。
本文仅对交叉熵算法做一个简短的介绍,详细的理论以及推导可参考 [9]。总体结构而言,交叉熵算法采用蒙地卡罗和重要采样方法解决随机组合优化问题。起初,该方法是用于解决小概率事件的概率估计的问题。通过将连续优化问题转换成小概率事件概率估计问题,交叉熵算法可解决包含大量局部最优值的连续全局优化问题。
假设优化问题的目标是获得使目标函数 取得最小值的最优值 ,即
(3)
换言之,公式(3)是寻找最优值 使得 , 表示最优的目标函数值。假设随机样本服从一定的概率分布函数 。此时,我们把求解优化问题的最小值转换为求解事件 的概率问题。具体来说, 的求解可转换成 事件中z的最大值的求解,此时的概率估计用 表示,即
(4)
表示服从概率分布函数 的样本, 。 表示指示变量,当事件 成立时取值1,其他情况取值0。当z越来越接近最优值 时,满足事件 的样本非常少,概率 的取值非常小,因此优化问题的求解转换成小概率事件的概率估计问题。
由此引出了下述的通用交叉熵算法求解步骤。首先,产生服从某个含有参数的概率分布函数的随机样本。然后,根据已有的样本,计算各个样本对应的PI目标函数值,按照从小到大排序,并且根据获得较小PI函数值的样本的特点更新概率分布函数中参数,由此让下一次迭代中产生更多的“优质样本”。通过这样的迭代过程,产生的样本质量得到不断的提高,并且向着最优值不断靠拢,直到不再有提升产生。由此确定的最优值就是优化问题的全局优值。简而言之,最优值应该在概率分布函数不断产生聚拢在 附近的样本时找到。本文采用的迭代停止条件是样本的标准方差不再减少,既小于某个值 。
据上所述,交叉熵算法的伪代码如下所述:
1) 迭代计数器k初始化为0,并令概率分布函数的参数 。
2) 当 生成一系列服从概率分布函数 的随机样本 ,( ),并且计算各个样本的目标函数值 。将得到的PI值从小到大排序,并且挑选取得最小目标值的 (一般 取0.05)作为重要样本,用 表示,同时令 等于排序好的 分为的目标函数值。
3) 利用重要样本 的相关信息更新概率分布函数的参数 ,使得 取最小值,用 表示。更新参数的原则如下所述:
(5)
这里的 作为平滑指数,一般取值范围为 ,本文取 。
4) 计数器k加1,并返回第二步,直到满足预设的迭代停止条件。
4. 跟驰模型标定的目标函数
跟驰模型的标定的本质是参数的最优值的搜索,参数的最优值存在于使得跟驰模型产生的驾驶数据与观测所得的驾驶数据的差异最小。本文中采取相对指标衡量模型数据与观测数据之间的差值,即
(6)
式中, 表示在时间间隔t智能驾驶模型的参数为X时产生的与前车的空间间距, 表示在时间间隔t观测所得的空间间距, 表示仿真总时长。这里的驾驶数据选取两车之间的空间间距是因为速度误差会随着空间间距误差的减少而减少,反过来则不成立。值得注意的是,式(6)对较小的空间间距更为敏感,即该目标函数更有利于重现慢行甚至停止的交通行为。
5. 案例分析
5.1. 标定合成路径数据
在这个例子中,利用合成的路径数据进行标定,用于验证交叉熵算法搜索全局最优值的有效性。合成的路径数据是通过预设前车数据和智能驾驶模型的参数得到的。具体来说,先设置前车的微观驾驶数据,然后利用预设好参数的智能驾驶模型跟着该前车的交通行为仿真一遍,把相关的驾驶信息记录下来,从而得到合成的路径信息。此时,再利用合成的路径信息标定智能驾驶模型,观测得到的最优值参数是否与预设的参数相近或者相等。
本例中预设的参数集为 ,各个参数对应智能驾驶模型的参数依次为最大加速度,期望减速度,期望速度,期望时间间隔,最小空间间距。利用得到的合成路径数据进行标定,采用相对指标(目标函数为式(6)),得到的最优值及相对误差如表1所示,相应的驾驶数据的对比图如图1所示。
除了期望减速度和期望速度,交叉熵标定的参数与全局最优值的相对误差都小于5%,体现了交叉熵算法具有精确地搜索全局最优值的能力。期望减速度和期望速度的较大相对误差,可能是因为在智能驾驶模型中,这两个参数对于目标函数值不太敏感,换句话说,期望减速度和期望速度的改变不会引起目标函数的较大变化,因此与全局最优值有较大的误差。值得注意的是,标定得到的驾驶数据,包括位置数据,空间间隔数据,速度数据,都表现出与观测数据几乎一致的特性,表明交叉熵算法可用于合成信息的标定,并且标定后的模型可以完全重现合成驾驶信息。
5.2. 标定NGSIM路径数据
NGSIM路径数据收集的是加利福利亚州内名为Interstate 80高速公路的一段路径,时间是从下午4点到4点15分,日期是2005年4月13号。该路段由6条车道和一条汇流闸道组成。在这个例子中,我们随机挑选了该路径上的一对跟车对作为标定数据源,验证交叉熵算法在标定实测路径数据的有效性。得到的结果如表2和图2所示。
Table 1. The calibration result with synthetic data
表1. 标定合成路径数据得到的最优值和相对误差
Table 2. The calibration result with NGSIM data
表2. 标定NGSIM数据得到的最优值和相对误差
 位置数据 空间间隔数据 速度数据
位置数据 空间间隔数据 速度数据
Figure 1. The comparison between simulated data and synthetic data
图1. 标定合成路径数据得到的仿真数据与观测数据的对比图
 位置数据 空间间隔数据 速度数据
位置数据 空间间隔数据 速度数据
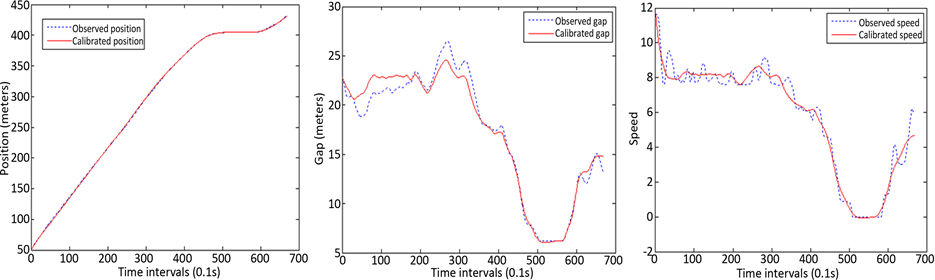
Figure 2. The comparison between simulated data and NGSIM data
图2. 标定NGSIM路径数据得到的仿真数据与观测数据的对比图
标定得到的参数最优值在其各自的物理意义中看似都是合理的。观测图2可知,标定后的跟驰模型产生的驾驶数据保持与观测数据高度的一致性,证实了交叉熵算法在标定实测路径数据的有效性。值得注意的是,在时间间隔500~600中,标定后的智能交通模型可以精确地重现停止的交通行为。
6. 结束语
利用标定后的跟驰模型精确地模拟驾驶员的驾驶行为将为分析和预测交通流特征提供极大的帮助。本文对跟驰模型的标定方法进行了研究,提出了基于交叉熵算法的跟驰模型标定框架。以智能驾驶模型为例,合成路径数据的标定实例验证了交叉熵算法搜索全局最优值的能力,NGSIM路径数据的标定实例体现了交叉熵算法应用于实测驾驶数据标定的有效性。
利用合成数据标定后的跟驰模型可完美重现相关的驾驶数据,而实测数据标定后的跟驰模型的模拟结果与实测值之间存在一定的误差,这可能是因为跟驰模型是众多驾驶员中总结出共性并用数学方法对其进行描述的数学模型,能够反应一般车辆运行的大体趋势,但对具体驾驶行为的细节部分可能会存在偏差。往后,我们将对标定后的跟驰模型进行灵敏度分析,探讨哪些参数的随机性会是造成偏差的主要原因。
致谢
感谢深圳市科技计划项目(项目编号GGFW2016033017241891,项目名称“深圳市交通大数据公共技术服务平台”)和深圳市战略性新兴产业发展专项资金2017年第一批扶持计划(项目名称:深圳市交通碳排放工程实验室,批复文号:深发改〔2017〕550号)的资助。
文章引用
傅恺延,丘建栋,潘嘉杰. 基于交叉熵算法的跟驰模型标定
Calibration of Car-Following Model Based on Cross-Entropy Method[J]. 建模与仿真, 2018, 07(02): 96-102. https://doi.org/10.12677/MOS.2018.72012
参考文献
- 1. Barcelo, J. (2010) Fundamentals of Traffic Simulation. Springer, Berlin. https://doi.org/10.1007/978-1-4419-6142-6
- 2. Saifuzzaman, M. and Zheng, Z. (2014) Incorporating Human-Factors in Car-Following Models: A Review of Recent Developments and Research Needs. Transportation Research Part C, 48, 379-403. https://doi.org/10.1016/j.trc.2014.09.008
- 3. Ngoduy, D. and Maher, M. (2012) Calibration of Second Order Traffic Models Using Continuous Entropy Method. Transportation Research Part C, 24, 102-121. https://doi.org/10.1016/j.trc.2012.02.007
- 4. Ciuffo, B. and Punzo, V. (2014) “No Free Lunch” Theorems Applied to the Calibration of Traffic Simulation Models. IEEE Transactions Intelligent Transportation System, 15, 1298-1309. https://doi.org/10.1109/TITS.2014.2302674
- 5. Zhong, R., Chen, C., Andy, C., Pan, T., Yuan, F. and He, Z. (2014) Automatic Calibration of Fundamental Diagram for First-Order Macroscopic Freeway Traffic Models. Journal of Advanced Transportation, 50, 363-385.
- 6. Rahman, M., Chowdhury, M., Khan, T. and Bhavsar, P. (2015) Improving the Efficacy of Car-Following Models with a New Stochastic Parameter Estimation and Calibration Method. IEEE Transport Intelligent Transportation System, 16, 2687-2699. https://doi.org/10.1109/TITS.2015.2420542
- 7. Zhong, R., Fu, K., Sumalee, A., Ngoduy, D. and Lam, W.H.K. (2016) A Cross-Entropy Method and Probabilistic Sensitivity Analysis Framework for Calibrating Microscopic Traffic Models. Transportation Research Part C, 63, 147-169. https://doi.org/10.1016/j.trc.2015.12.006
- 8. He, D. and Lee, L. (2010) Simulation Optimization Using the Cross-Entropy Method with Optimal Computing Budget Allocation. ACM Transactions on Modeling and Computer Simulation, 20, 1-22. https://doi.org/10.1145/1667072.1667076
- 9. Kroese, D., Rubinstein, R. and Glynn P. (2013) The Cross-Entropy Method for Estimation. Handbook of Statistics, Vol. 31, Elsevier B.V., Chennai, 19-34.
- 10. Treiber, M. and Kesting, A. (2014) Microscopic Calibration and Validation of Car-Following Models: A Systematic Approach. Procedia-Social and Behavioral Sciences, 80, 922-939. https://doi.org/10.1016/j.sbspro.2013.05.050
- 11. Maher, M., Liu, R. and Ngoduy, D. (2013) Signal Optimisation Using the cross Entropy Method. Transportation Research Part C, 27, 76-88. https://doi.org/10.1016/j.trc.2011.05.018
